Subtracting Polynomials
Subtract like terms by changing the signs of the terms being subtracted, and following the rules for adding polynomials.

Below are several different ways to attack this example:
Example 1: Subtract (2x2 + 4x – 6) from (x2 – 4)
Solution:
Horizontal Method:
Notice the order of this subtraction. Just as is done when subtracting signed numbers, change the signs of the terms being subtracted (or distribute -1), and follow the rules for adding signed like terms.
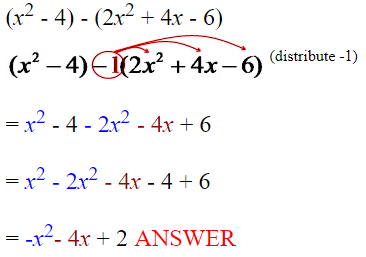
Vertical Method:
Again, notice the order of the subtraction. Change the signs of the terms being subtracted, and follow the rules for adding signed like terms. In this problem, we insert 0x to hold the missing column for x.
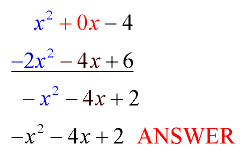
Read More:
- What is a Polynomial?
- Types of Polynomials
- Monomials, Binomials, and Polynomials
- Adding Polynomials
- Dividing Polynomials
- Polynomials – Long Division
- Degree (of an Expression)
- Special Binomial Products
- Multiplying Binomials
- Difference of Two Cubes
- Polynomial Remainder Theorem
- Factoring in Algebra
- Factorization of Polynomials Using Factor Theorem
- How do you use the factor theorem?
- How to factorise a polynomial by splitting the middle term?
- Review Factoring Polynomials
- Zeros of a Polynomial Function
- Factors and Coefficients of a Polynomial
- Roots of Polynomials: Sums and Products
- Review Factoring Polynomials
- Solving Polynomial Equations of Higher Degree
- Examining Graphs of Polynomial Equations of Higher Degree