How To Factorise A Polynomial By Splitting The Middle Term

Factorise A Polynomial By Splitting The Middle Term Example Problems With Solutions

Type I: Factorization of Quadratic polynomials of the form x² + bx + c.
(i) In order to factorize x² + bx + c we have to find numbers p and q such that p + q = b and pq = c.
(ii) After finding p and q, we split the middle term in the quadratic as px + qx and get desired factors by grouping the terms.

Example 1:    Factorize each of the following expressions:
(i) x² + 6x + 8               (ii) x² + 4x –21
Solution:
(i) In order to factorize x²  + 6x + 8, we find two numbers p and q such that p + q = 6 and pq = 8.
Clearly, 2 + 4 = 6 and 2 × 4 = 8.
We know split the middle term 6x in the given quadratic as 2x + 4x, so that
x²    + 6x + 8 = x²  + 2x + 4x + 8
= (x²  + 2x) + (4x + 8)
= x (x + 2) + 4 (x+ 2)
= (x + 2) (x + 4)
(ii) In order to factorize x²  + 4x – 21, we have to find two numbers p and q such that
p + q = 4 and pq = – 21
Clearly, 7 + (– 3) = 4 and 7 × – 3 = – 21
We now split the middle term 4x of
x²  + 4x – 21 as 7x – 3x, so that
x²  + 4x – 21 = x²  + 7x – 3 x – 21
= (x²  + 7x) – (3x + 21)
= x (x + 7) – 3 (x + 7) = (x + 7) (x – 3)

Example 2:    Factorize each of the following quadratic polynomials:   x² – 21x + 108
Solution:    In order to factorize x² – 21x + 108,
we have to find two numbers such that their sum is – 21 and the product 108.
Clearly, – 21 = – 12– 9 and – 12 × – 9 = 108
x² – 21 x + 108 = x² – 12 x – 9x + 108
= (x² – 12 x) – (9x– 108)
= x(x – 12) – 9 (x – 12) = (x–12) (x – 9)

Example 3:    Factorize the following by splitting the middle term :  x² + 3 √3 x + 6
Solution:    In order to factorize x² + 3 √3 x + 6, we have to find two numbers p and q such that

Type II: Factorization of polynomials reducible to the form x² + bx + c.

Example 4:    Factorize (a² – 2a)² – 23(a² – 2a) + 120.
Solution:

Example 5:    Factorize the following by splitting the middle term x⁴– 5x² + 4
Solution:
Let x² = y. Then, x⁴ – 5x² + 4
= y² – 5 y + 4
Now, y² – 5 y + 4
= y² – 4y – y + 4
= (y² – 4y) – (y – 4)
= y(y –4) – (y– 4)
= (y – 4) (y – 1)
Replacing y by x² on both sides, we get
x⁴ – 5x² + 4 = (x²–4) (x² – 1)
= (x²–2²) (x² – 1²) = (x–2) (x+2) (x – 1) (x + 1)

Example 6:    Factorize (x² – 4x) (x² – 4x – 1) – 20
Solution:
The given expression is
(x² – 4x) (x² – 4x – 1) – 20
= (x² – 4x)² – (x² – 4x) – 20
Let x² – 4x = y . Then,
(x² – 4x)² – (x² – 4x) – 20 = y² – y – 20
Now, y² – y – 20
= y² –5 y + 4y – 20
= (y² – 5 y) + (4y– 20)
= y (y – 5) + 4 (y – 5)
= (y – 5) (y + 4)
Thus, y² – y – 20 = (y – 5) (y + 4)
Replacing y by x² – 4x on both sides, we get
(x² – 4x)² – (x² – 4x) – 20
= (x² – 4x – 5) (x² – 4x +4)
= (x² – 5x + x – 5) (x² – 2 × x × 2 + 2²)
= {x (x – 5) + (x – 5)} (x – 2)²
= (x – 5) (x + 1) (x – 2)²

Type III: Factorization of Expressions which are not quadratic but can factorized by splitting the middle term.

Example 7:    If x² + px + q = (x + a) (x + b), then factorize x² + pxy + qy².
Solution:    We have,
x² + px + q = (x + a) (x + b)
⇒ x² + px + q = x² + x(a + b) + ab
On equating the coefficients of like powers of x, we get
p = a + b and q = ab
∴ x² + pxy + qy² = x² + (a + b)xy + aby²
= (x² + axy) + (bxy + aby²)
= x(x + ay) + by(x + ay)
= (x + ay) (x + by)

Example 8:    Factorize the following expression x²y² – xy – 72
Solution:
In order to factorize x²y² – xy – 72, we have to find two numbers p and q such that
p+ q = – 1 and pq = – 72
clearly, – 9 +8 = – 1 and – 9 × 8 = – 72.
So, we write the middle term – xy of
x²y² – xy – 72 as – 9 xy + 8 xy, so that
x²y² – xy – 72 = x²y² – 9 xy + 8 xy – 72
= (x²y2² – 9xy) + (8xy – 72)
= xy (xy – 9) + 8 (xy – 9)
= (xy – 9) (xy + 8)

Factorization Of Polynomials Of The Form ax² + bx + c, a ≠ 0, 1

Type I: Factorization of quadratic polynomials of the form ax² + bx + c, a 0, 1
(i) In order to factorize ax² + bx + c. We find numbers l and m such that l + m = b and lm = ac
(ii) After finding l and m, we split the middle term bx as lx + mx and get the desired factors by grouping the terms.

Example 9:    Factorize the following expression
6x² – 5 x – 6
Solution:    The given expression is of the form ax²+ bx+c, where, a = 6, b = – 5 and c = –6.
In order to factorize the given expression, we have to find two numbers l and m such that
l + m = b = i.e., l + m = – 5
and lm = ac i.e. lm = 6 × – 6 = – 36
i.e., we have to find two factors of – 36
such that their sum is – 5. Clearly,
– 9 + 4 = – 5 and – 9 × 4 = – 36
l = – 9 and m = 4
Now, we split the middle term – 5x of
x² – 5x – 6 as – 9 x + 4x, so that
6x² – 5x – 6 = 6x²–9x + 4x – 6
= (6x² – 9x) + (4x – 6)
= 3x (2x – 3) + 2(2x – 3) = (2x – 3) (3x + 2)

Example 10:    Factorize each of the following expressions:
(i) √3 x² + 11x + 6 √3
(ii) 4 √3 x² + 5x – 2 √3
(iii) 7 √2 x² – 10 x – 4 √2
Solution:   (i) The given quadratic expression is of the form ax² + bx + c,
where a = √3, b = 11 and c = 6 √3.
In order to factorize it, we have to find two numbers l and m such that

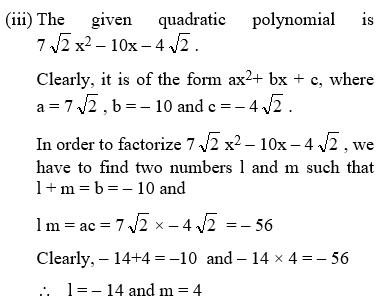
Example 11:    Factorize the following by splitting the middle term
1/3 x² – 2x – 9
Solution:    

Type II: Factorization of trinomial expressions which are not quadratic but can be factorized by splitting the middle term.

Example 12:    Factorize the following trinomial by splitting the middle term
8a³ – 2a²b – 15 ab²
Solution:    Here a³ × ab² = (a²b)² i.e., the product of the variables in first and last term is same as the square of the variables in the middle term. So, in order to factorize the given trinomial, we split the middle term
– 2a²b as – 12a²b + 10 a²b , so that
8a³ – 2a²b – 15 ab²
= 8a³ –12a²b +10 a²b–15 ab²
= 4a²(2a – 3b) + 5 ab (2a – 3b)
= (2a – 3b) (4a² + 5ab)
= (2a – 3b) a (4a + 5b)
= a (2a – 3 b) (4a + 5b)

Type III : Factorization of trinomial expressions reducible to quadratic expressions.

Example 13:    Factorize each of the following expressions by splitting the middle term :
(i) 9(x – 2y)²– 4(x – 2y) – 13
(ii) 2(x + y)² – 9(x + y) – 5
(iii) 8(a + 1)² + 2(a + 1) (b + 2) – 15(b + 2)²
Solution:    (i) The given expression is 9(x – 2y)² – 4(x – 2y) – 13.
Putting x – 2y = a, we get
9(x – 2y)² – 4(x – 2y) – 13 = 9a² – 4a – 13
Now, 9a² – 4a – 13 = 9a² – 13a + 9a – 13
= (9a² – 13a) + (9a – 13)
= a(9a – 13) + (9a – 13)
= (a + 1) (9a – 13)
Replacing a by x – 2y on both sides, we get
9(x – 2y)² – 4(x – 2y) – 13
= (x – 2y + 1) {9(x – 2y) – 13}
= (x – 2y + 1) (9x – 18y – 13)
(ii) The given expression is
2(x + y)² – 9(x + y) – 5
Replacing x + y by a in the given expression, we have
2(x + y)² – 9(x + y) – 5 = 2a² – 9a – 5
Now, 2a² – 9a – 5 = 2a² – 10a + a – 5
= (2a² – 10a) + (a – 5)
= 2a(a – 5) + (a – 5) = (a – 5) (2a + 1)
Replacing a by x + y on both sides, we get
2(x + y)² – 9(x + y) – 5
= (x + y – 5) {2(x + y) + 1}
= (x + y – 5) (2x + 2y + 1).
(iii) The given trinomial is
8(a + 1)² + 2(a + 1) (b + 2) – 15(b + 2)²
Putting a + 1 = x and b + 2 = y, we have
8(a + 1)² + 2(a + 1) (b + 2) – 15(b + 2)²
= 8x² + 2xy – 15y²
= 8x² + 12xy – 10xy – 15y²
= 4x(2x + 3y) – 5y(2x + 3y)
= (2x + 3y) (4x – 5y)
Replacing x by a + 1 and y by b + 2, we get
8(a + 1)² + 2(a + 1) (b + 2) – 15(b + 2)²
= {2(a + 1) + 3(b + 2)} {4(a + 1) – 5(b +2)}
= (2a + 3b + 8) (4a – 5b – 6)