Review Factoring Polynomials
This lesson will review the process of factoring, which is used when solving equations and simplifying rational expressions.
To factor polynomial expressions, there are several approaches that can be used to simplify the process. While all of these approaches are not used for each problem, it is best to examine your expression for the possible existence of these situations. Ask yourself the following questions:
Are there Common Factors?
Factor out the Greatest Common Factor (GCF) of the expression, if one exists. This will make it simpler to factor the remaining expression.
Take care NOT to drop this GCF, as it is still part of the expression’s answer.

Does the expression have only 2 terms?
If it does, is the expression a DIFFERENCE of PERFECT SQUARES?
If so, you should be able to write the expression as a product of the sum and difference of the square roots of the terms.
Sometimes, as in Example 2 below, it is best to write the terms in square notation so
you can see what the terms will be in factored form. Be sure to use parentheses!
This process is also called Factoring with DOTS (Difference of Two Squares).

Does the expression have exactly 3 terms?
If yes, then the expression may factor into the product of two binomials. One way to solve this type of problem is to use trial and error, keeping certain “hints” in mind.
Hints:
With the trinomial arranged in proper order (highest to lowest powers):
- if the leading coefficient is 1, you are looking for two numbers that multiply to the last term and add to the coefficient of the middle term.
- if the leading coefficient is not 1, you will have to look more carefully to find the answer. See Factoring Trinomials () – Set Up, Guess and Check Method and Factoring by Grouping Method.
For the examples below, use the hint above for factoring when the leading coefficient is 1, and the trial and error (guess and check) method when the leading coefficient is 2.
Always check your work by multiplying the binomials to see if your center term matches the original problem.

Special trinomial: Perfect Square
Consider what happens when a binomial is squared:
where the center term is twice the product of a and b.
If you can recognize this pattern, it is very easy to factor a trinomial that is the perfect square of a binomial.

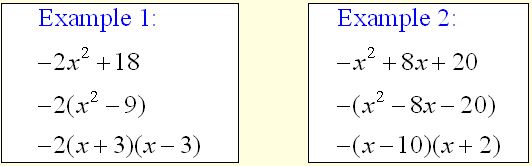
Does the first term have a Negative Coefficient?
If yes, then factor out the negative sign first, using the common factor method at the top of this page.
Remember, if the leading term has a coefficient of (- 1), and there are
NO other common terms, then the GCF is = -1.