Division Algorithm For Polynomials
If p(x) and g(x) are any two polynomials with
g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that
p(x) = q(x) × g(x) + r(x)
where r(x) = 0 or degree of r(x) < degree of g(x).
The result is called Division Algorithm for polynomials.
Dividend = Quotient × Divisor + Remainder
Polynomials – Long Division
Working rule to Divide a Polynomial by Another Polynomial:
Step 1: First arrange the term of dividend and the divisor in the decreasing order of their degrees.
Step 2: To obtain the first term of quotient divide the highest degree term of the dividend by the highest degree term of the divisor.
Step 3: To obtain the second term of the quotient, divide the highest degree term of the new dividend obtained as remainder by the highest degree term of the divisor.
Step 4: Continue this process till the degree of remainder is less than the degree of divisor.

People also ask
Division Algorithm For Polynomials With Examples
Example 1: Divide 3x3 + 16x2 + 21x + 20 by x + 4.
Sol.
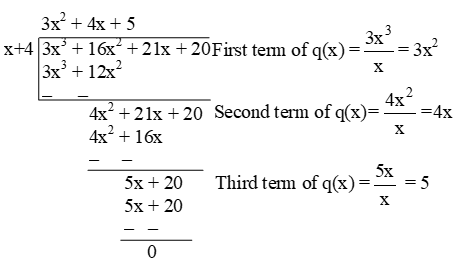
Quotient = 3x2 + 4x + 5
Remainder = 0
Example 2: Apply the division algorithm to find the quotient and remainder on dividing p(x) by g(x) as given below :
p(x) = x3 – 3x2 + 5x – 3 and g(x) = x2 – 2
Sol. We have,
p(x) = x3 – 3x2 + 5x – 3 and g(x) = x2 – 2
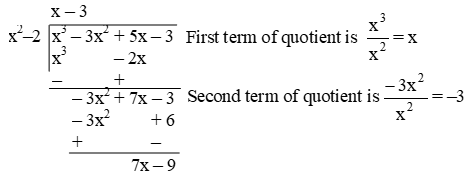
We stop here since
degree of (7x – 9) < degree of (x2 – 2)
So, quotient = x – 3, remainder = 7x – 9
Therefore,
Quotient × Divisor + Remainder
= (x – 3) (x2 – 2) + 7x – 9
= x3 – 2x – 3x2 + 6 + 7x – 9
= x3 – 3x2 + 5x – 3 = Dividend
Therefore, the division algorithm is verified.
Example 3: Apply the division algorithm to find the quotient and remainder on dividing p(x) by g(x) as given below
p(x) = x4 – 3x2 + 4x + 5, g (x) = x2 + 1 – x
Sol. We have,
p(x) = x4 – 3x2 + 4x + 5, g (x) = x2 + 1 – x
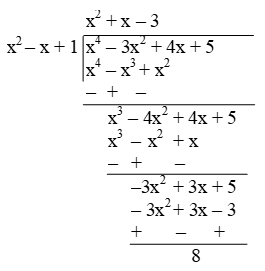
We stop here since
degree of (8) < degree of (x2 – x + 1).
So, quotient = x2 + x – 3, remainder = 8
Therefore,
Quotient × Divisor + Remainder
= (x2 + x – 3) (x2 – x + 1) + 8
= x4 – x3 + x2 + x3 – x2 + x – 3x2 + 3x – 3 + 8
= x4 – 3x2 + 4x + 5 = Dividend
Therefore the Division Algorithm is verified.
Example 4: Check whether the first polynomial is a factor of the second polynomial by applying the division algorithm. t2 – 3; 2t4 + 3t3 – 2t2 – 9t – 12.
Sol. We divide 2t4 + 3t3 – 2t2 – 9t – 12 by t2 – 3
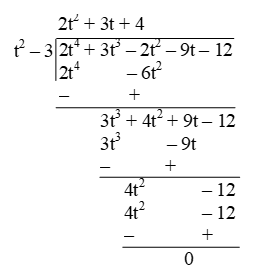
Here, remainder is 0, so t2 – 3 is a factor of 2t4 + 3t3 – 2t2 – 9t – 12.
2t4 + 3t3 – 2t2 – 9t – 12 = (2t2 + 3t + 4) (t2 – 3)
Example 5: Obtain all the zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\).
Sol. Since two zeroes are \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\)
x = \(\sqrt{\frac{5}{3}}\), x = \(-\sqrt{\frac{5}{3}}\)
\(\Rightarrow \left( \text{x}-\sqrt{\frac{5}{3}} \right)\left( \text{x +}\sqrt{\frac{5}{3}} \right)={{\text{x}}^{2}}-\frac{5}{3}\) Or 3x2 – 5 is a factor of the given polynomial.
Now, we apply the division algorithm to the given polynomial and 3x2 – 5.

So, 3x4 + 6x3 – 2x2 – 10x – 5
= (3x2 – 5) (x2 + 2x + 1) + 0
Quotient = x2 + 2x + 1 = (x + 1)2
Zeroes of (x + 1)2 are –1, –1.
Hence, all its zeroes are \(\sqrt{\frac{5}{3}}\), \(-\sqrt{\frac{5}{3}}\), –1, –1.
Example 6: On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and –2x + 4, respectively. Find g(x).
Sol. p(x) = x3 – 3x2 + x + 2 q(x) = x – 2 and r (x) = –2x + 4
By Division Algorithm, we know that
p(x) = q(x) × g(x) + r(x)
Therefore,
x3 – 3x2 + x + 2 = (x – 2) × g(x) + (–2x + 4)
⇒ x3 – 3x2 + x + 2 + 2x – 4 = (x – 2) × g(x)
\(\Rightarrow g(\text{x})=\frac{{{\text{x}}^{3}}-3{{\text{x}}^{2}}+3\text{x}-2}{\text{x}-2}\)
On dividing x3 – 3x2 + x + 2 by x – 2,
we get g(x)

Hence, g(x) = x2 – x + 1.
Example 7: Give examples of polynomials p(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg q(x) = 0
Sol.
(i) Let q(x) = 3x2 + 2x + 6, degree of q(x) = 2
p(x) = 12x2 + 8x + 24, degree of p(x) = 2
Here, deg p(x) = deg q(x)
(ii) p(x) = x5 + 2x4 + 3x3+ 5x2 + 2
q(x) = x2 + x + 1, degree of q(x) = 2
g(x) = x3 + x2 + x + 1
r(x) = 2x2 – 2x + 1, degree of r(x) = 2
Here, deg q(x) = deg r(x)
(iii) Let p(x) = 2x4 + x3 + 6x2 + 4x + 12
q(x) = 2, degree of q(x) = 0
g(x) = x4 + 4x3 + 3x2 + 2x + 6
r(x) = 0
Here, deg q(x) = 0
Example 8: If the zeroes of polynomial x3 – 3x2 + x + 1 are a – b, a , a + b. Find a and b.
Sol. ∵ a – b, a, a + b are zeros
∴ product (a – b) a(a + b) = –1
⇒ (a2 – b2) a = –1 …(1)
and sum of zeroes is (a – b) + a + (a + b) = 3
⇒ 3a = 3 ⇒ a = 1 …(2)
by (1) and (2)
(1 – b2)1 = –1
⇒ 2 = b2 ⇒ b = ± √2
∴ a = –1 & b = ± √2
Example 9: If two zeroes of the polynomial x4 – 6x3 –26x2 + 138x – 35 are 2 ± √3, find other zeroes.
Sol. ∵ 2 ± √3 are zeroes.
∴ x = 2 ± √3
⇒ x – 2 = ±(squaring both sides)
⇒ (x – 2)2 = 3 ⇒ x2 + 4 – 4x – 3 = 0
⇒ x2 – 4x + 1 = 0 , is a factor of given polynomial
∴ other factors \(=\frac{{{\text{x}}^{4}}-6{{\text{x}}^{3}}-26{{\text{x}}^{2}}+138\text{x}-35}{{{\text{x}}^{2}}-4\text{x}+1}\)

∴ other factors = x2 – 2x – 35
= x2 – 7x + 5x – 35 = x(x – 7) + 5(x – 7)
= (x – 7) (x + 5)
∴ other zeroes are (x – 7) = 0 ⇒ x = 7
x + 5 = 0 ⇒ x = – 5
Example 10: If the polynomial x4 – 6x3 + 16x2 –25x + 10 is divided by another polynomial x2 –2x + k, the remainder comes out to be x + a, find k & a.
Sol.

According to questions, remainder is x + a
∴ coefficient of x = 1
⇒ 2k – 9 = 1
⇒ k = (10/2) = 5
Also constant term = a
⇒ k2 – 8k + 10 = a ⇒ (5)2 – 8(5) + 10 = a
⇒ a = 25 – 40 + 10
⇒ a = – 5
∴ k = 5, a = –5