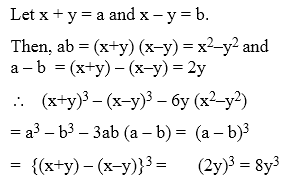What Are The Types Of Factorization

Types Of Factorization Example Problems With Solutions

Type I: Factorization by taking out the common factors. 

Example 1:    Factorize the following expression
2x²y + 6xy² + 10x²y²
Solution:    2x²y + 6xy² + 10x²y²
=2xy(x + 3y + 5xy)

Type II: Factorization by grouping the terms.   

Example 2:    Factorize the following expression
a² – b + ab – a
Solution:    a² – b + ab – a
= a² + ab – b – a = (a² + ab) – (b + a)
= a (a + b) – (a + b) = (a + b) (a – 1)

Type III: Factorization by making a perfect square.  

Example 3:    Factorize of the following expression
9x² + 12xy + 4y²
Solution:    9x² + 12xy + 4y²
= (3x)² + 2 × (3x) × (2y) + (2y)²
= (3x + 2y)²

Example 4:    Factorize of the following expression
\(\frac{{{x}^{2}}}{{{y}^{2}}}+2+\frac{{{y}^{2}}}{{{x}^{2\prime }}},x\ne 0,y\ne 0\)
Solution:    

Example 5:    Factorize of the following expression
\({{\left( 5x-\frac{1}{x} \right)}^{2}}+4\left( 5x-\frac{1}{x} \right)+4,x\ne 0\)
Solution:

People also ask:

• Solving Quadratic Equations with Complex Roots
• Factoring Quadratics
• Solving Quadratic Equations by Factoring
• Solving Factorable Quadratic Equations
• Completing the Square
• Solving Quadratic Equations by Completing the Square

Type IV: Factorizing by difference of two squares.

Example 6:    Factorize the following expressions
(a) 2x²y + 6 xy² + 10 x²y²
(b) 2x⁴ + 2x³y + 3xy² + 3y³
Solution:

Example 7:    Factorize 4x² + 12 xy + 9 y²
Solution:

Example 8:    Factorize each of the following expressions
(i) 9x² – 4y²
(ii) x³ – x
Solution:

Example 9:    Factorize each of the following expressions
(i) 36x² – 12x + 1 – 25y²
\(\text{(ii) }{{a}^{2}}-\frac{9}{{{a}^{2}}},a\ne 0\)
Solution:

Example 10:    Factorize the following algebraic expression
x⁴ – 81y⁴
Solution:

Example 11:    Factorize the following expression
x(x+z) – y (y+z)
Solution:    x(x+z) – y (y+z) = (x² – y²) + (xz–yz)
= (x–y) (x+y) + z (x–y)
= (x–y) {(x+y) + z}
= (x–y) (x+ y + z)

Example 12:    Factorize the following expression
x⁴ + x² + 1
Solution:    x⁴ + x² + 1 = (x⁴ + 2x² +1) – x²
= (x² +1)² – x² = (x² + 1 – x) (x² + 1+x)
= (x²–x + 1) (x² + x + 1)

Type V: Factorizing the sum and difference of cubes of two quantities.
(i) (a³ + b³) = (a + b) (a² – ab + b²)
(ii) (a³ – b³) = (a – b) (a² + ab + b²)

Example 13:    Factorize the following expression
a³ + 27
Solution:   a³  + 27 = a³  + 3³ = (a + 3) (a² –3a +9)

Example 14:    Simplify : (x+ y)³ – (x –y)³ – 6y(x² – y²)
Solution: