Selina Concise Physics Class 10 ICSE Solutions Calorimetry APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 10 Physics Chapter 11 Calorimetry. You can download the Selina Concise Physics ICSE Solutions for Class 10 with Free PDF download option. Selina Publishers Concise Physics for Class 10 ICSE Solutions all questions are solved and … [Read more...] about Selina Concise Physics Class 10 ICSE Solutions Calorimetry
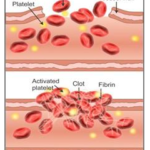
Selina Concise Biology Class 10 ICSE Solutions The Circulatory System
Selina Concise Biology Class 10 ICSE Solutions The Circulatory System APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 10 Biology Chapter 7 The Circulatory System. You can download the Selina Concise Biology ICSE Solutions for Class 10 with Free PDF download option. Selina Publishers Concise Biology for Class 10 ICSE Solutions all … [Read more...] about Selina Concise Biology Class 10 ICSE Solutions The Circulatory System
HSSLive Plus Two Study Material / Question Bank Kerala
We are providing HSE Kerala Board Syllabus HSSLive Higher Secondary SCERT Plus Two Study Material, Question Bank, Quick Revision Notes, Chapter Wise Notes, Chapter Wise Previous Year Important Questions and Answers, Previous Year Sample Question Papers with Answers based on CBSE NCERT syllabus in both English Medium and Malayalam Medium for Class 12.Students can also get … [Read more...] about HSSLive Plus Two Study Material / Question Bank Kerala
ML Aggarwal ICSE Solutions for Class 7 Maths Chapter 13 Practical Geometry
ML Aggarwal ICSE Solutions for Class 7 Maths Chapter 13 Practical Geometry ML Aggarwal SolutionsICSE SolutionsSelina ICSE SolutionsUnderstanding ICSE Mathematics Class 7 ML Aggarwal Solutions Pdf Download Chapter 13 Practical Geometry … [Read more...] about ML Aggarwal ICSE Solutions for Class 7 Maths Chapter 13 Practical Geometry
ML Aggarwal ICSE Solutions for Class 7 Maths Chapter 3 Rational Numbers
ML Aggarwal ICSE Solutions for Class 7 Maths Chapter 3 Rational Numbers ML Aggarwal SolutionsICSE SolutionsSelina ICSE SolutionsUnderstanding ICSE Mathematics Class 7 ML Aggarwal Solutions Pdf Download Chapter 3 Rational Numbers … [Read more...] about ML Aggarwal ICSE Solutions for Class 7 Maths Chapter 3 Rational Numbers