Special Pattern Binomials
The following are special multiplications involving binomials that you will want to try to remember. Be sure to notice the patterns in each situation. You will be seeing these patterns in numerous problems.
Don’t panic! If you cannot remember these patterns, you can arrive at your answer by simply multiplying with the distributive method. These patterns are, however, very popular. If you can remember the patterns, you can save yourself some work.
Let’s examine these patterns:
Squaring a Binomial – multiplying times itself
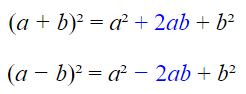In each pattern, the middle term is twice the multiplication of the terms used to create the binomial expression. Notice how the sign of the middle term is positive in (a + b)2, and negative in (a – b)2.
Example 1: (x + 4)2
(x + 4)2
= (x + 4)(x + 4)
= x2 + 4x + 4x + 16
= x2 + 8x + 16
Example 2: (2x – 3)2
(2x – 3)2
= (2x – 3)(2x – 3)
= 4x2 – 6x – 6x + 9
= 4x2 – 12x + 9
Product of Sum and Difference
(notice that the binomials differ only by the sign between the terms)
(a + b)(a – b) = a2 – b2
Notice that there appears to be no “middle” term to forma a trinomial answer, as was seen in the problems above. When multiplication occurs, the values that would form the middle term of a trinomial actually add to zero.
(a + b)(a – b) = a2 – ab + ab – b2 = a2 – b2
[-ab + ab = 0ab]
Example 3: (x + 2)(x – 2)
(x + 2)(x – 2)
= x2 – 4x + 4x – 4
= x2 – 4
Example 4: (2a + 5)(2a – 5)
(2a + 5)(2a – 5)
= 4a2 – 10a + 10a – 25
= 4a2 – 25