Monomials, Binomials, and Polynomials
- A monomial is the product of non-negative integer powers of variables. Consequently, a monomial has NO variable in its denominator. It has one term. (mono implies one)

(notice: no negative exponents, no fractional exponents) - A binomial is the sum of two monomials. It has two unlike terms.
(bi implies two)

- A trinomial is the sum of three monomials. It has three unlike terms. (tri implies three)

- A polynomial is the sum of one or more terms. (poly implies many)

Polynomials are in simplest form when they contain no like terms.
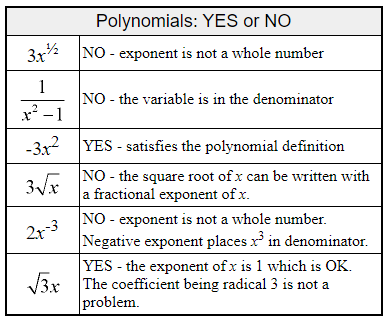
Polynomials are generally written in descending order.

Read More:
- What is a Polynomial?
- Types of Polynomials
- Adding Polynomials
- Subtracting Polynomials
- Dividing Polynomials
- Polynomials – Long Division
- Degree (of an Expression)
- Special Binomial Products
- Multiplying Binomials
- Difference of Two Cubes
- Polynomial Remainder Theorem
- Factoring in Algebra
- Factorization of Polynomials Using Factor Theorem
- How do you use the factor theorem?
- How to factorise a polynomial by splitting the middle term?
- Review Factoring Polynomials
- Zeros of a Polynomial Function
- Factors and Coefficients of a Polynomial
- Roots of Polynomials: Sums and Products
- Review Factoring Polynomials
- Solving Polynomial Equations of Higher Degree
- Examining Graphs of Polynomial Equations of Higher Degree