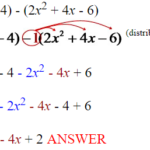Glencoe Algebra 1 Solutions Chapter 8 Polynomials Glencoe Mathematics Algebra 1 Answer Key Glencoe Algebra 1 Solutions Chapter 8 PolynomialsAnswer 1PT. Answer 1STP. Answer 1VC. Answer 2PT. Answer 2STP. Answer 2VC. Answer 3PT. Answer 3STP. Answer…

Zeros Of A Polynomial FunctionIf for x = a, the value of the polynomial p(x) is 0 i.e., p(a) = 0; then x = a is a zero of the polynomial p(x).For Example: (i) For polynomial p(x) = x – 2; p(2) = 2 – 2 = 0 ∴ x = 2 or simply 2 is a zero of the polynomial p…

Types Of Polynomials(i) Based on degree : If degree of polynomial isExamples1.One  Linearx + 3, y – x + 2, √3x –32.TwoQuadratic2x2 –7, \(\frac{1}{3}{{\text{x}}^{2}}+{{\text{y}}^{2}}-2\text{xy}\), x2 +1+ 3y3.ThreeCubicx3 + 3x2 –7x+8, 2x2+5x3+7,4.Fourbi-qu…

Subtracting PolynomialsSubtract like terms by changing the signs of the terms being subtracted, and following the rules for adding polynomials. Below are several different ways to attack this example:Example 1: Subtract (2x2 + 4x – 6) from (x2 – 4) Solu…

Algebraic ExpressionAny combination of literal numbers or variables and numbers (numerals) connected by +, –, × or ÷ signs is called an algebraic expression. For example, 5, 6x, a + b × c, 4 × m + n, x – y ÷ z are algebraic expressions. The perimeter P o…

Adding PolynomialsIn the previous lesson, we are discussing about polynomials, Types of Polynomials, Monomials, Binomials, and Polynomials . Now lets learn adding polynomials. Add like terms by adding the numerical portion of the terms, following the ru…

Factors And Coefficients Of A PolynomialFactor:  When numbers (constants) and variables are multiplied to form a term, then each quantity multiplied is called a factor of the term. A constant factor is called a numerical factor while a variable factor i…

Factorise A Polynomial By Splitting The Middle Term Example Problems With SolutionsType I: Factorization of Quadratic polynomials of the form x2 + bx + c. (i) In order to factorize x2 + bx + c we have to find numbers p and q such that p + q = b and pq = …

Algebraic Identities Of PolynomialsYou can also read https://www.aplustopper.com/ncert-solutions-for-class-10-maths-chapter-2/ for more solved examples. People also askDivision algorithm for polynomialsFactorization of polynomials using factor theorem A…

Polynomials In One VariableIf a polynomial has only one variable then it is called polynomial in one variable. P(x) = 2x3 + 5x – 3                            Cubic trinomial Q(x) = 7x7 – 5x5 – 3x3 + x + 3    polynomial of degree 7 R(y) = y              …