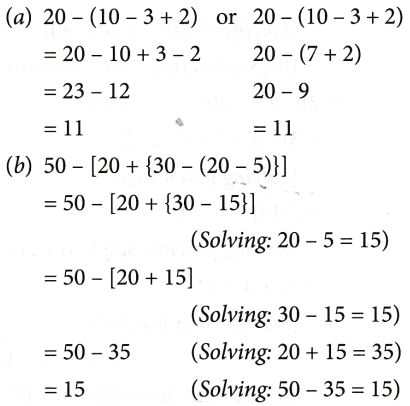OPERATIONS ON NUMBERS
Addition
Addition of two or more numbers gives us another number. The numbers which are added are called addends and the new number thus obtained is called the sum. For example,
34670 + 12345 = 47015
Here, 34670 and 12345 are called addends and 47015 is called the sum of 34670 and 12345. Large numbers are added in the same way as the small numbers.
Addition by grouping
When we add three numbers, we can add any two numbers first and then add the third number to the sum. In other words, we can group any two of the three numbers in order to find the sum of the three numbers. If we have to add more than three numbers, we can similarly group any two of the given numbers in several ways and add them. For example, suppose we want to add 234523, 123098, 555623, and 876543. We can find the sum in any of the following ways:
- [(234523 + 123098) + 555623] + 876543
= (357621 + 555623) + 876543
= 913244 + 876543 = 1789787 - [(234523 + 123098) + 876543] + 555623
= (357621 + 876543) + 555623
= 1234164 + 555623 = 1789787
So, we can add three or more numbers by grouping them in any way we feel convenient.
Subtraction
Subtraction of one number from another number gives us a third number. The new number thus obtained is called the difference of the two numbers. For example,
70000 – 67429 =2571
Here, 2571 is the difference of 70000 and 67429. Large numbers are subtracted in the same way as the small numbers.
Read More:
- Integers and Examples
- Fundamental Operations on Integers
- Whole Numbers And Its Properties
- Hints for Remembering the Properties of Real Numbers
- Order of Operations and Evaluating Expressions
- Absolute Value
Multiplication
Multiplication of two or more numbers gives us another number. The new number thus obtained is called the product of those numbers. For example, 11 × 13 = 143.
Here, 143 is the product of 11 and 13. 11 and 13 are called the/actors of 143. Note that 1 is always a factor of any number.
Let us take another example, say, 855 × 73 = 62415. Here, 855 and 73 are factors of 62415, and 62415 is the product of 855 and 73.
Large numbers are multiplied in the same way as the small numbers.
Multiplication using zeros
When we multiply a number by 10,100,1000, etc. we simply place those many zeros on the right of that number. For example, if we want to multiply 15 by 10, then the answer will be 150. Similarly, if we want to multiply 15 by 100, then the answer will be 1500, and so on. Zeros have been added on the right side of 15.
Division
Division of a number by another number gives two new numbers—the quotient and the remainder. The number that is divided is called the dividend and the number that divides is called the divisor. For example,
Here, 7 is the divisor; 66 is the
dividend; 9 is the quotient, and 3 is the remainder.
Divide 69205 by 432 and find the quotient and remainder.
Here, the quotient is 160 and remainder is 85.
Mixed operations involving +, –, ×, and ÷
Till now we have solved problems involving only one type of operation, that is, one of the following: addition, subtraction, division, and multiplication. But what do we do if a problem involves two or more operations together? Consider the following problem:
Example: Simplify: 16 – 6 + 2 – 3
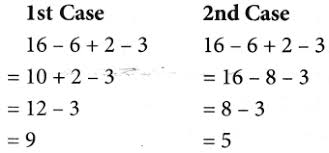
In the 1st case, the answer is 9 and in the 2nd case, it is 5. We get different answers depending on the order in which the operations are carried out. But one of the two answers we got is wrong. In order to avoid this kind of ambiguity, an international convention has been accepted.
- If any mathematical expression has symbols of addition and subtraction both, we first add and then subtract. For example, consider the following case: 16 – 3 + 4 – 5
= 20 – 3 – 5 (Addition: 16 + 4 = 20)
= 17 – 5 (Subtraction: 20 – 3 = 17)
= 12 (Subtraction: 17 – 5 = 12) - If in three operations [(+, – , and × ) or (+, – , and ÷)], that is, besides addition and subtraction, a problem involves multiplication or division, we first multiply or divide, and then go for addition and subtraction respectively. For example, consider the following cases.
(a) Simplify: 7 + 3 × 4 – 3
In the above example, the three operations involved are +, – , and ×. To solve this problem, we first multiply the numbers, then we go for addition, and at the end we subtract.
7 + 3 × 4 – 3
= 7 + 12 – 3 (Multiplication: 3 × 4 = 12)
= 19 – 3 (Addition: 7 + 12 = 19)
= 16 (Subtraction: 19 – 3 = 16)
(b) Simplify: 16 – 6 ÷ 2 + 8
In the above example, the three operations involved are +, – , and ÷. To solve this problem, we first divide, then add, and at the end subtract the number. 16 – 6 ÷ 2 + 8
= 16 – 3 + 8 (Division: 6 ÷ 2 = 3)
= 24 – 3 (Addition: 16 + 8 = 24)
= 21 (Subtraction: 24 – 3 = 21) - When a problem involves all the operations namely, +, – , × , and ÷, then there is an agreed formula denoted by ‘DMAS’, which mathematicians follow. In ‘DMAS’, D stands for division, M for multiplication, A for addition, and S for subtraction. DMAS represents the order of operations. For example, consider the following cases.
(a) Simplify: 5 + 4 × 3 – 9 ÷ 3
In the above example, all the four operations are there, so we have to use DMAS rule, as shown below: 5 + 4 × 3 – 9 ÷ 3
= 5 + 4 × 3 – 3 (Division: 9 ÷ 3 = 3)
= 5 + 12 – 3 (Multiplication: 4 × 3 = 12)
= 17 – 3 (Addition: 5 + 12 = 17)
= 14 (Subtraction: 17 – 3 = 14)
(b) Simplify: 7 × 3 – 4 + 60 ÷ 10
In this example too, all the four operations are there, hence to simplify this we have to use DMAS rule. 7 × 3 – 4 + 60 ÷ 10
= 7 × 3 – 4 + 6 (Division: 60 ÷ 10 = 6)
= 21 – 4 + 6 (Multiplication: 7 × 3 = 21)
= 27 – 4 (Addition: 21 + 6 = 27)
= 23 (Subtraction: 27 – 4 = 3)
Using the operation ‘Of’
Sometimes we need to find the value of ‘\(\frac { 1 }{ 2 }\) of 16’ or ‘3 of 5’.
This means we need to find the value of \(\frac { 1 }{ 2 }\) × 16 or 3 × 5.
So ‘of’ means multiplication.
Hence, \(\frac { 1 }{ 2 }\) of 16 = \(\frac { 1 }{ 2 }\) × 16
= 8
and 3 of 5 =3 × 5
= 15.
When the operation ‘of’ appears in any mathematical expression, then it must be performed before any other operation. To solve such kind of expression we use ODMAS rule, in which O stands for of, D for division, M for multiplication, A for addition, and S for subtraction.
Consider the following examples.
Example 1: Simplify 36 ÷ 2 of 3 + 6 × 2.
Solution: To solve this, we first solve the operation ‘of’.
36 ÷ 2 of 3 + 6 × 2
= 36 ÷ 6 + 6 × 2 (Of. 2 of 3 = 2 × 3 = 6)
= 6 + 6 × 2 (Division: 36 ÷ 6 = 6)
= 6 + 12 (Multiplication: 6 × 2 = 12)
= 18 (Addition: 6 + 12 = 18)
Example 2: Simplify 42 ÷ 6 × 2 + \(\frac { 1 }{ 7 }\) of 35 × 2.
Solution: 42 ÷ 6 × 2 + \(\frac { 1 }{ 7 }\) of 35 × 2
= 42 ÷ 6 × 2 + 5 × 2 (Of: \(\frac { 1 }{ 7 }\) of 35 = \(\frac { 1 }{ 7 }\) × 35 = 5)
= 7 × 2 + 5 × 2 (Division: 42 ÷ 6 = 7)
= 14 + 10 (Multiplication: 7 × 2 = 14 and 5 × 2 = 10)
= 24 (Addition: 14 + 10 = 24)
Use of brackets and the BODMAS rule
Let us consider an example to illustrate the use of brackets.
Rima bought 35 chocolates and ate 5 of them. She distributed the remaining chocolates equally among 6 of her friends. How many chocolates did she give to each of them?
In this problem we have to subtract 5 chocolates that Rima ate, from 35 chocolates she had, before dividing them among 6 of her friends. So we have to first perform the operation of subtraction and then do division. In such cases, we use brackets around the part that has to be done first, that is
(35 – 5) ÷ 6 (First solve bracket, i.e., 35 – 5 = 30)
= 30 ÷ 6 (Division: 30 ÷ 6 = 5)
= 5
Consider another example.
Example 3: Solve 2 of 3 × (5 + 2).
Solution: 2 of 3 × (5 + 2)
= 2 of 3 × 7 (First bracket: 5 + 2 = 7)
= 6 × 7 (Of: 2 of 3 = 2 × 3 = 6)
= 42 (Multiplication: 6 × 7 = 42)
Hence, when problems involve brackets, of, ×, ÷, +, and – then
To make it easy to remember this order, we remember the word BODMAS, where B stands for brackets, O for of’, D for division, M for multiplication, A for addition, and S for subtraction. This is called the ‘BODMAS‘ rule.
Sometimes numerical expressions may involve different types of brackets. These brackets are
- Vinculum or bar —
- Parentheses or small brackets ( )
- Braces or curly brackets { }
- Square brackets or big brackets [ ]
We simplify expressions by starting with the innermost bracket. Usually the vinculum is the innermost bracket, next is the parentheses, then the braces, and finally the square brackets. Let us now consider some examples.
Example 4: Simplify \(25-[20-\{10-(7-\overline{5-3})\}]\).
Solution:
RULES FOR SIMPLIFICATION
1. Order of operation: The use of brackets take us to a new order of operation. The operation inside the brackets comes before the ODMAS. There are different types of brackets already mentioned here.
2. If there is no sign between a number and the bracket, then it is implied that the operation to be performed is multiplication.
Examples
3. When there is ‘+’ sign before a bracket, you can simply remove the bracket.
Examples:
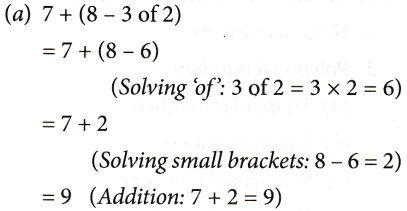
4. When there is a ‘–’ sign before a bracket, then all signs within the bracket change while removing the bracket.
Examples:
