Hints for Remembering the Properties of Real Numbers
Commutative Property – interchange or switch the elements
Example shows commutative property for addition:
X + Y = Y + X
Think of the elements as “commuting” from one location to another. “They get in their cars and drive to their new locations.” This explanation will help you to remember that the elements are “moving” (physically changing places).

Associative Property – regroup the elements
Example shows associative property for addition:
(X + Y) + Z = X + (Y + Z)
The associative property can be thought of as illustrating “friendships” (associations). The parentheses show the grouping of two friends. In the example below, the red girl (y) decides to change from the blue boyfriend (x) to the green boyfriend (z). “I don’t want to associate with you any longer!” Notice that the elements do not physically move, they simply change the person with whom they are “holding hands” (illustrated by the parentheses.)
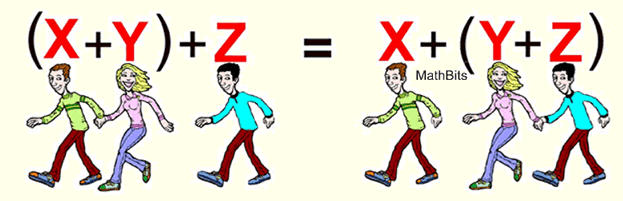
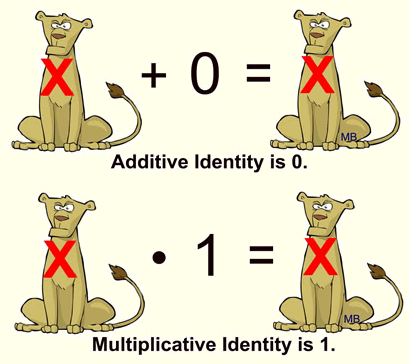
Identity Property – What returns the input unchanged?
X + 0 = X Additive Identity
X • 1 = X Multiplicative Identity
Try to remember the “I” in the word identity. Variables can often times have an “attitude”. “I am the most important thing in the world and I do not want to change!” The identity element allows the variable to maintain this attitude.
Inverse Property – What brings you back to the identity element using that operation?
X + -X = 0 Additive Inverse
X • 1/X = 1 Multiplicative Inverse
Think of the inverse as “inventing” an identity element. What would you need to add (multiply) to this element to turn it into an identity element?

Distributive Property – multiply across the parentheses. Each element inside the parentheses is multiplied by the element outside the parentheses.
a(b + c) = a•b + a•c
Let’s consider the problem 3(x + 6). The number in front of the parentheses is “looking” to distribute (multiply) its value with all of the terms inside the parentheses.
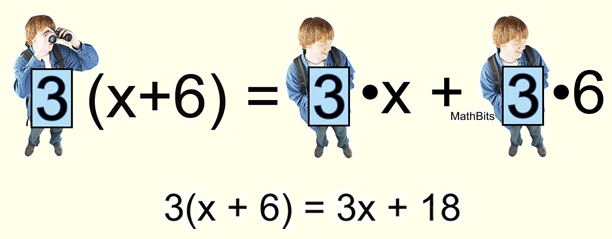
Read More:
- Integers and Examples
- Fundamental Operations on Integers
- Whole Numbers And Its Properties
- Hints for Remembering the Properties of Real Numbers
- What Are The Four Basic Operations In Mathematics
- Order of Operations and Evaluating Expressions
- Absolute Value