What is an Integer and give some Examples
Introduction

While studying the properties of whole numbers, we found that the closure property does not hold good for the subtraction of natural numbers as well as whole numbers. This is because of the following:
12 – 10 = 2 is a whole number as well as a natural number.
12-12 = 0 is a whole number but not a natural number.
12 – 18 = – 6 which is neither a whole number nor a natural number.
Let us study an example
Rohit bought 3 basketballs from a wholesale sports goods shop for Rs 200 each. He sold the first basketball for Rs 220, the second basketball for Rs 200, and the third basketball for Rs 195. On the first basketball, he gained Rs. 20, i.e., Rs. 220 – Rs 200 = + Rs 20; on the second basketball he did not gain anything, i.e., Rs 200 – Rs 200 = Rs 0; on the third basketball, he lost Rs 5, i.e., Rs 195 – Rs 200 = – Rs 5.
Similarly, in our daily life we come across so many situations such as:
(i) 2°C rise in temperature or 2°C fall in temperature.
(ii) Rs 200 profit or Rs 200 loss
(iii) 4 km above the sea level or 4 km below the sea level etc.
In the above cases, the idea of oppositeness has been introduced. To avoid confusion or mistakes.
Read More:
- Fundamental Operations on Integers
- Whole Numbers
- RS Aggarwal Class 6 Solutions Integers
- RS Aggarwal Class 7 Solutions Integers
Opposite of Natural numbers
In mathematics, Rs. 200 profit means +200 and Rs. 200 loss means -200, +2°C means 2°C rise in temperature and -2°C means 2°C fall in temperature, +4 km means 4 km above the sea level and – 4 km means 4 km below the sea level. Similarly, in natural numbers, the opposite of 1 is -1, opposite of 2 is -2, opposite of 3 is -3, and so on.
We, therefore, need to extend the whole number system to include such ‘negative numbers’ which are opposite of natural numbers. In order to have opposites of 1, 2, 3,… we introduce -1, -2, -3,…. All the numbers with ‘+ve’ sign are called positive numbers and all the numbers with ‘-ve’ sign are called negative numbers. Zero is neither positive nor negative.
This new collection of numbers are called integers which include all positive numbers, negative numbers, and zero. Numbers 1, 2, 3,… are called positive integers and -1, -2, -3,… are called negative integers.
Note:
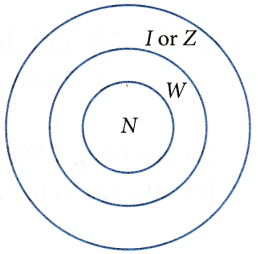
Set of negative numbers, positive numbers, and zero together are called integers.
Natural numbers (N) = 1, 2, 3,4,…
Whole numbers (W) = 0,1,2, 3,…
Integers (Z or I) = -3, -2, -1, 0,1, 2, 3 ,…
Ordering of Integers
We know that a whole number is greater than any whole number to its left on a number line. Same is true for the integers also. The number line given below shows whole numbers and negative numbers with zero in the middle.

All the positive integers (which are greater than zero) lie on the right side of zero and all the negative integers (which are less than zero) lie on the left side of zero at equal distance from each other. A number placed to the right of another is greater than it.
Examples:
7 > 3 as 7 is to the right of 3.
0 > -1 as 0 is to the right of-1.
Note:
1 is the smallest positive integer but -1 is the largest negative integer, e., -1 is always greater than -2, -4,…
From the examples, we note that:
(a) Since 0 is to the right of every negative integer, so 0 is greater than every negative integer.
(b) Since 0 is to the left of every positive integer, so 0 is less than every positive integer.
(c) Every positive integer is to the right of every negative integer. Hence positive integers are greater than negative integers.
(d) The greater the number is the lesser to its opposite.
Absolute value of integers
The absolute value of an integer is its numerical value regardless of its sign. It indicates its size or magnitude. So, absolute value is either zero or positive. It is never negative. The absolute value of 6 is written as | 6 | = 6 and absolute value of -5 = | -5 | = 5.
Note that | 0 | = 0; |-117 | = 117; but – | 117 | = -117.
Example 1: Write the opposite of each of the following:
(a) 6 km north
(b) 14 km above the sea level
(c) Depositing money in the bank Solution
(a) 6 km south
(b) 14 km below the sea level
(c) Withdrawing money from the bank
Example 2: Find the absolute value of | -51 | and -I 13 |.
Solution: Absolute value of (-51) is | -51 | = 51 Absolute value of -| 13 | = -13