What is the Relationship Between Temperature and Volume of a Gas
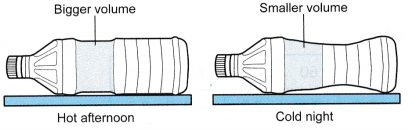
- A woman left an empty water bottle in the car on a hot day. When she opened the door of her car at night, she felt the air in the car was cold and found the bottle compressed, as shown in Figure.
- Charles’ law gives the relationship between the volume and the temperature of a fixed mass of gas at constant pressure.
- The relationship between the volume and the temperature can be explained using the kinetic theory of gases.
(a) When a gas in a closed container is heated, the average kinetic energy of the molecules increases. The temperature of the gas increases.
(b) The rate of collision between the molecules and the walls of the container will increase if the volume is constant.
(c) If the gas is allowed to expand, the faster molecules now move in a bigger space.
(d) Therefore, the rate of collision between the molecules and the walls remains constant and thus, the pressure is constant.
(e) For a gas which is heated, to remain at constant pressure, the gas must be allowed to expand and increase its volume. - Charles’ law states that for a fixed mass of gas, the volume of the gas is directly proportional to its absolute temperature when its pressure is kept constant.
- The mathematical expression for Charles’ law:
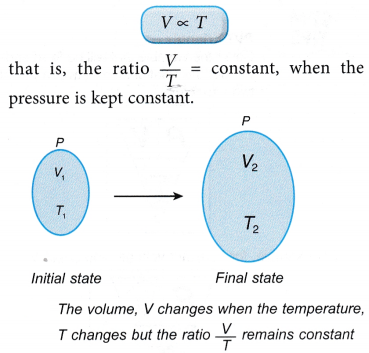
- Consider a gas with an initial volume, V1 and temperature, T1. When the temperature changes to T2, the volume of the gas changes to V2.
According to Charles’ law:
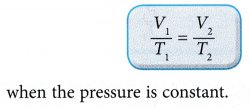
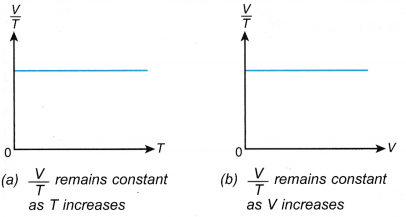
- The relationship between the volume and the absolute temperature of a gas under constant pressure can also be expressed with the graphs in Figure.
People also ask
What is the Boyle’s law?
What is the Pressure Law?
Experiment:
Aim: To determine the relationship between the volume and the temperature of a fixed mass of gas at constant pressure.
Problem: What is the relationship between the volume and the temperature of a fixed mass of gas at constant pressure?
Inference: The temperature of a gas affects its volume.
Hypothesis: The volume of a fixed mass of gas increases when the temperature is increased if the pressure is kept constant.
Variables:
(a) Manipulated variable: Temperature
(b) Responding variable: The volume of the air
(c) Fixed variables: The mass of the air in the capillary tube and the pressure
Operational Definition:
(a) The thermometer measures the temperature of the water. Since the water and the air in the capillary tube are in thermal equilibrium, the reading of the thermometer is defined operationally as the temperature of the air in the capillary tube.
(b) The volume of the air in the capillary tube is directly proportional to the length of the air column as the cross-sectional area of the tube is uniform. Therefore, the length of the air column is defined operationally to represent the volume of the air.
Materials: Concentrated sulphuric acid, some rubber bands
Apparatus: Capillary tube, thermometer, 600 ml beaker, wooden ruler, stirrer, tripod stand with wire gauze, Bunsen burner, retort stand with clamp
Method:
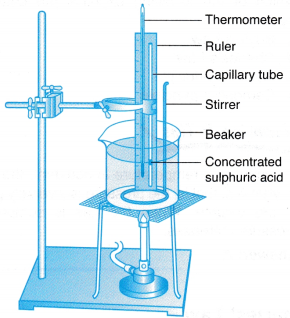
- The apparatus is set up as shown in Figure.
- The water in the beaker is heated slowly and stirred continuously.
- When the temperature, θ = 30°C, the length of the air column, l is read on the ruler scale.
- Steps 2 and 3 are repeated for values of temperature, θ = 40°C, 50°C, 60°C, 70°C, 80°C and 90°C.
- The readings are tabulated. A graph of length of air column, l against temperature, θ is plotted.
Results:
- Tabulation of results.

- Graph of length of air column, l against temperature θ,

Discussion:
- The water was stirred continuously so that its temperature remained uniform.
- The graph of the length of the air column, l against the temperature, θ in °C is a straight line which does not pass through the origin. At 0°C, the molecules are still moving randomly and the air has a certain volume.
- When the straight line is extrapolated, it is found that the volume is expected to become zero at -273°C or the absolute zero of temperature.
- A graph of the length of the air column, l against absolute temperature, T is a straight line passing through the origin as shown in Figure.

Conclusion:
The volume of the gas is directly proportional to its absolute temperature. The hypothesis is accepted.
Charles’ Law Example Problems with Solutions
Example 1. Figure (a) shows an enclosed plastic bag containing 3.0 cm3 of air at a temperature of 2.0°C in a refrigerator. When the plastic bag was taken out and placed in a room where the temperature was 27.0°C, ) the air in it expanded, as shown in Figure (b).
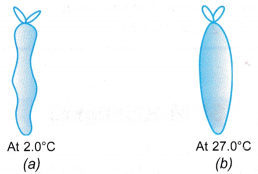
Calculate the final volume of the air in the plastic bag.
Solution:
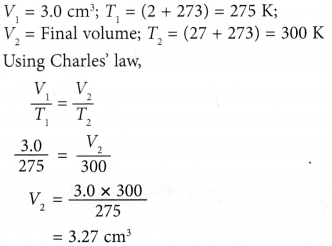
Example 2. Figure shows air trapped in an overturned empty crate floating on the sea. The volume of the air is 160 cm3 when the temperature of the sea water is 35.0°C.
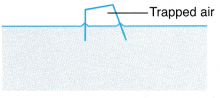
What is the temperature of the sea water, when the volume of the trapped air is 150 cm3?
Solution:
