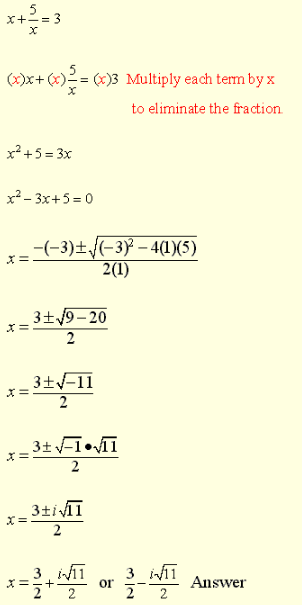Solving Quadratic Equations with Complex Roots
When the roots of a quadratic equation are imaginary, they always occur in conjugate pairs.
A root of an equation is a solution of that equation.
If a quadratic equation with real-number coefficients has a negative discriminant, then the two solutions to the equation are complex conjugates of each other.
(Remember that a negative number under a radical sign yields a complex number.)
The discriminant is the b2- 4ac part of the quadratic formula (the part under the radical sign).
If the discriminant is negative, when you solve your quadratic equation the number under the radical sign in the quadratic formula is negative — forming complex roots.
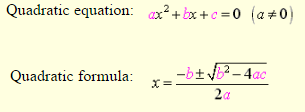
Example 1:
Find the solution set of the given equation over the set of complex numbers.

Example 2:
Find the solution set of the given equation over the set of complex numbers.
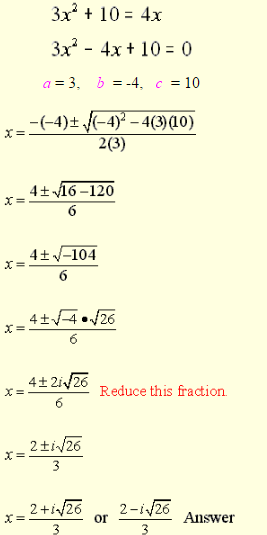
Example 3:
Find the solution set of the given equation and express its roots in a+bi form.