How do you calculate the total resistance of a series circuit?

How do you calculate the total resistance of a series circuit?

The Effective Resistance of Resistors Connected in Series

1. There are three important characteristics in a series circuit:
   (a) The current passing through each resistor is the same.
   (b) The potential difference across each resistor depends directly on its resistance.
   (c) The sum of the potential difference across each resistor is equal to the total potential difference of the source.
   
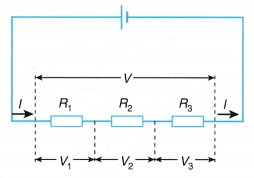
2. When two or more resistances are joined end-to-end so that the same current flows through each of them, they are said to be connected in series. When a series combination of resistances is connected to a battery, the same current (I) flows through each of them.
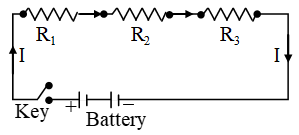   When a series combination of resistances is connected to a battery, the same current (I) flows through each of them.
3. Law of combination of resistances in series: The law of combination of resistances in series states that when a number of resistances are connected in series, their equivalent resistance is equal to the sum of the individual resistances. Thus, if R₁, R₂, R₃ …, etc. are combined in series, then the equivalent resistance (R) is given by,
   R = R₁ + R₂ + R₃ + …                          …. (i)
4. Derivation of mathematical expression of resistances in series combination:
   Let, R₁, R₂ and R₃ be the resistances connected in series, I be the current flowing through the circuit, i.e., passing through each resistance, and V₁, V₂ and V₃ be the potential difference across R₁, R₂ and R₃ respectively. Then, from Ohm’s law,
   V₁ = IR₁, V₂ = IR₂ and V₃ = IR₃      … (ii)
5. If, V is the potential difference across the combination of resistances then,
   V = V₁ + V₂ + V₃                                 … (iii)
6. If, R is the equivalent resistance of the circuit, then
   V = IR                                                   … (iv)
7. Using Equations (i) to (iv) we can write,
   IR = V = V₁ + V₂ + V₃
   IR = IR₁ + IR₂ + IR₃
   IR = I (R₁ + R₂ + R₃ )
   R = R₁ + R₂ + R₃
   Therefore, when resistances are combined in series, the equivalent resistance is higher than each individual resistance.
8. The equivalent circuit is shown in Figure.
   

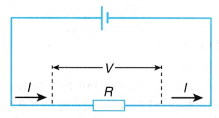
Some results about series combination:

1. When two or more resistors are connected in series, the total resistance of the combination is equal to the sum of all the individual resistances.
2. When two or more resistors are connected in series, the same current flows through each resistor.
3. When a number of resistors are connected in series, the voltage across the combination
   (i.e. voltage of the battery in the circuit), is equal to the sum of the voltage drop
   (or potential difference) across each individual resistor.

People also ask

• How series and parallel circuits are different?
• How do you calculate the total resistance of a parallel circuit?
• What is Electric Current?
• What is an electric field and how is it created?
• What is the Relationship between Electric Current and Potential Difference?
• Electromotive Force, Internal Resistance & Potential Difference of a Cell/Battery
• Relationship between Energy Transferred, Current, Voltage and Time
• Power Rating and Energy Consumption of Various Electrical Appliances

Series Circuit Problems with Solutions

1. Three resistors, R₁, R₂ and R₃, are connected in series to a 6 V battery as shown in Figure.
   
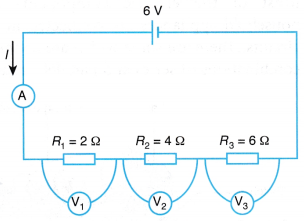
   Calculate
   (a) the effective resistance, R of the circuit,
   (b) the current, I in the circuit,
   (c) the potential differences across each resistor, V₁, V₂ and V₃.
   Solution:
   
   Note that the larger the resistance, the larger the potential difference across it. The sum of the potential difference across each resistor is the same as the potential difference across the battery.