What is Power
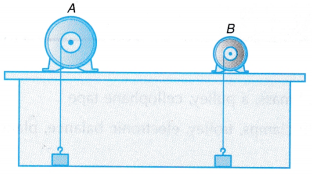Figure shows two electric motors, A and B respectively. Each motor lifts an identical load from the floor.
Motor A can lift the load more quickly than motor B. Hence, motor A can do the same amount of work in a shorter time.
Motor A is said to be more powerful than motor B.
Definition: Power is defined as the rate of doing work.
\( \text{Power}=\frac{\text{Work}\,\text{done}}{\text{Time}\,\text{taken}} \)
\( \text{P}=\frac{\text{W}}{\text{t}} \)
In other words, power is the work done per unit time, power is a scalar quantity.
Since W = F.S therefore
\( \text{P}=\frac{\text{W}}{\text{t}}=\frac{\text{FS}}{\text{t}}=F\times V=\text{force}\times \text{velocity} \)
Unit of power: The S.I. unit of power is watt and it is the rate of doing work at 1 joule per second.
\(1\text{ watt}=\frac{\text{1}\,\text{joule}}{\text{1}\,\text{seconds}}\)
1 kilowatt = 1 kW = 1000 W
1 Horse power = 1 H.P. = 746 W
Activity 1
Aim: To measure the power generated by a student running up the stairs.
Apparatus: Stopwatch, metre rule, weighing machine
Method:
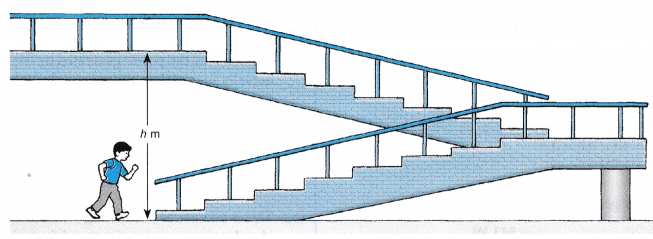
- The mass, m of a student is measured.
- The student is asked to run up the stairs from one floor to the next floor of a building in the school.
- The vertical height, h gained by the student in running up to the next floor is measured by multiplying the number of steps by the height of each step.
- The time taken, t for the run is recorded by another student using a stopwatch.
Analysis of Data:
Mass of student = m kg
Vertical height = h m
Time taken = t s
Work done = Gain in gravitational potential energy = mgh, where g = 9.8 m s-2
Power generated, P = W/t watt
Discussion:
- For a more accurate result, more than one person should time the run and the average time should be calculated.
- This activity assumes that all the work done goes to the increase in gravitational potential energy only. However, in reality, some work is also used in overcoming frictional forces.
What is the Efficiency?
- Useful energy is the energy that can be used to do a certain work.
- Wasted energy is the energy that is lost to the surrounding and cannot be used to do useful work.
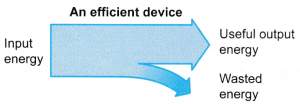
- Figure shows an efficient device. Most of the input energy is converted into useful energy. Very little of the input energy is wasted.
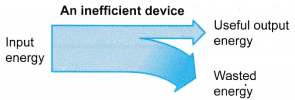
- Figure shows an inefficient device. Most of the input energy is wasted. Only a small portion of the input energy is converted into useful energy.
- The efficiency of a device is defined as the percentage of the input energy that is transformed into useful energy.
- The efficiency of a device can also be calculated in terms of power.
- In the engine of a vehicle as shown in Figure, the energy needed is obtained by burning fuels like petrol and diesel. The energy obtained is converted into kinetic energy of the car. However, a large portion of the energy is wasted.
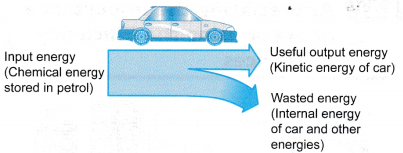
- There are two types of engines that are commonly used in vehicles; the petrol engine and the diesel engine. The efficiency of a diesel engine is higher than that of a petrol engine. However, diesel engines are heavier and more costly to construct. Diesel engines are generally noisier than petrol engines. Diesel engines are preferred by heavy vehicles like lorries, buses, tractors and locomotives.
- Electric vehicles are more efficient because less energy is wasted as heat. However, electric vehicles are not common because of the high cost of technology required to build them.
Power and Efficiency Example Problems with Solutions
Example 1. A machine raises a load of 750 N through a height of 15 m in 5s. Calculate:
(i) the work done by the machine.
(ii) the power at which the machine works.
Solution: (i) Work done is given by W = F.s
Here F = 750 N; s = 15 m
∴ W = 750 × 15 = 11250 J
= 11.250 kJ
(ii) Now, power of the machine is given by
\( \text{P}=\frac{\text{W}}{\text{t}} \)
Here, W = 11250 J; t = 5 s
∴ Power P = \(\frac { 11250J }{ 5s }\) = 2250 W = 2.250 kW
Example 2. A weight lifter lifted a load of 100 kg to a height of 3 m in 10 s. Calculate the following:
(i) amount of work done
(ii) power developed by him
Solution: (i) Work done is given by
W = F . s
Here, F = mg = 100 × 10 = 1000 N
W = 1000 N × 3 m = 3000 joule
(ii) Now, P = \(\frac { W }{ t }\) , where W = 3000 J and t = 10 s
∴ P = \(\frac { 3000J }{ 10s }\) = 300 W
Example 3. A water pump raises 60 liters of water through a height of 20 m in 5 s. Calculate the power of the pump. (Given: g = 10 m/s2, density of water = 1000 kg/m3)
Solution: Work done, W = F.s …(1)
Here, F = mg …(2)
But, Mass = volume × density
Volume = 60 liters = 60 × 10-3 m3
Density = 1000 kg/m3
∴ Mass, m = (60 × 10-3 m3) × (1000 kg/m3) = 60 kg
∴ Equation (2) becomes
F = 60 kg × 10 m/s2 = 600 N
Now, W = F . s = 600 N × 20 m = 12000 J
\( \text{P}=\frac{\text{W}}{\text{t}} \)
= \(\frac { 12000J }{ 5s }\) = 2400 W
Example 4. A woman pulls a bucket of water of total mass 5 kg from a well which is 10 m deep in 10 s. Calculate the power used by her.
Solution: Given that m = 5 kg; h = 10 m; t = 10 s
g = 10 m/s2
\( \text{P}=\frac{\text{W}}{\text{t}} \)
\(=\frac{\text{mgh}}{\text{t}}=\frac{\text{5 }\!\!\times\!\!\text{ 10 }\!\!\times\!\!\text{ 10}}{\text{10}}=\text{50W}\)
Example 5. A 40 kg boy climbs a vertical height of 3.5 m in 4 s.
(a) Calculate the gain in gravitational potential energy of the boy.
(b) Determine the power generated by the boy. [Take g=9.8m s-2]
Solution:
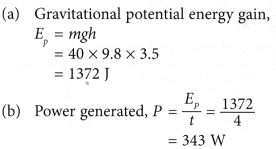
Example 6. A crane lifts a heavy bucket to a height of 2.5 m from the ground in 3.5 s.
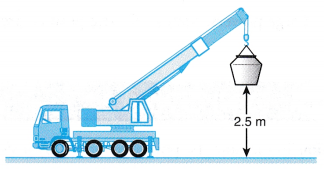
(a) Calculate the power generated by the crane in lifting the bucket if the mass of the bucket is 840 kg.
(b) Explain why the power generated by the crane is actually higher than the value calculated in (a), [g = 9.8 m s-2]
Solution:
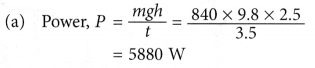
(b) This is because besides lifting the bucket, work is also done to overcome frictional forces between the cable and the pulley and other parts of the crane.
Example 7. An electric motor has an input power of 120 W. It lifts a 20 kg load to a vertical height of 1.5 m in 5 s. What is the efficiency of the electric motor? [g = 9.8 m s-2]
