What is the formula for work?
Definition: In our daily life “work” implies an activity resulting in muscular or mental exertion. However, in physics the term ‘work’ is used in a specific sense involves the displacement of a particle or body under the action of a force. “work is said to be done when the point of application of a force moves.
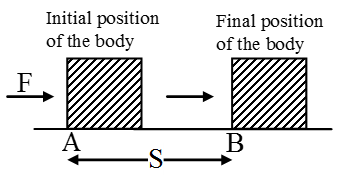
Work done in moving a body is equal to the product of force exerted on the body and the distance moved by the body in the direction of force.
Work = Force × Distance moved in the direction of force.
The work done by a force on a body depends on two factors
(i) Magnitude of the force, and
(ii) Distance through which the body moves (in the direction of force)
Unit of Work
When a force of 1 newton moves a body through a distance of 1 metre in its own direction, then the work done is known as 1 joule.
Work = Force × Displacement
1 joule = 1 N × 1 m
or 1 J = 1 Nm (In SI unit)
Work Done Analysis
Work done when force and displacement are along same line:
Work done by a force: Work is said to be done by a force if the direction of displacement is the same as the direction of the applied force.
Work done against the force: Work is said to be done against a force if the direction of the displacement is opposite to that of the force.
Work done against gravity: To lift an object, an applied force has to be equal and opposite to the force of gravity acting on the object. If ‘m’ is the mass of the object and ‘h’ is the height through which it is raised, then the upward force
(F) = force of gravity = mg
If ‘W’ stands for work done, then
W = F . h = mg . h
Thus W = mgh
Therefore we can say that, “The amount of work done is equal to the product of weight of the body and the vertical distance through which the body is lifted.
Work done when force and displacement are inclined (Oblique case):
Consider a force ‘F’ acting at angle θ to the direction of displacement ‘s’ as shown in fig.
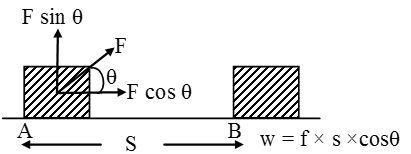
Work done when force is perpendicular to Displacement
θ = 90º
W = F.S × cos 90º = F.S × 0 = 0
Thus no work is done when a force acts at right angle to the displacement.
Special Examples
- When a bob attached to a string is whirled along a circular horizontal path, the force acting on the bob acts towards the centre of the circle and is called as the centripetal force. Since the bob is always displaced perpendicular to this force, thus no work is done in this case.
- Earth revolves around the sun. A satellite moves around the earth. In all these cases, the direction of displacement is always perpendicular to the direction of force (centripetal force) and hence no work is done.
- A person walking on a road with a load on his head actually does no work because the weight of the load (force of gravity) acts vertically downwards, while the motion is horizontal that is perpendicular to the direction of force resulting in no work done. Here, one can ask that if no work is done, then why the person gets tired. It is because the person has to do work in moving his muscles or to work against friction and air resistance.
Work Done By A Force Example Problems With Solutions
Example 1: How much work is done by a force of 10N in moving an object through a distance of 1 m in the direction of the force ?
Solution: The work done is calculated by using the formula:
W = F × S
Here, Force F = 10 N
And, Distance, S = 1 m
So, Work done, W = 10 × 1 J
= 10 J
Thus, the work done is 10 joules
Example 2: Find the work done by a force of 10 N in moving an object through a distance of 2 m.
Solution: Work done = Force × Distance moved
Here, Force = 10 N
Distance moved = 2 m
Work done, W = 10 N × 2 m
= 20 Joule = 20 J
Example 3: Calculate the work done in pushing a cart, through a distance of 100 m against the force of friction equal to 120 N.
Solution: Force, F = 120 N; Distance, s = 100 m
Using the formula, we have
W = Fs = 120 N × 100 m = 12,000 J
Example 4: A body of mass 5 kg is displaced through a distance of 4m under an acceleration of 3 m/s2. Calculate the work done.
Sol. Given: mass, m = 5 kg
acceleration, a = 3 m/s2
Force acting on the body is given by
F = ma = 5 × 3 = 15 N
Now, work done is given by
W = Fs = 15 N × 4 m = 60 J
Example 5: Calculate the work done in raising a bucket full of water and weighing 200 kg through a height of 5 m. (Take g = 9.8 ms-2).
Solution: Force of gravity
mg = 200 × 9.8 = 1960.0 N
h = 5 m
Work done, W = mgh
or W = 1960 × 5 = 9800 J
Example 6: A boy pulls a toy cart with a force of 100 N by a string which makes an angle of 60º with the horizontal so as to move the toy cart by a distance horizontally. Calculate the work done.
Solution: Given F = 100 N, s = 3 m, θ= 60º.
Work done is given by
W = Fs cos θ= 100 × 2 × cos 60º
= 100 × 3 × 1/2 = 150 J (∵ cos 60º = 1/2 )
Example 7: An engine does 64,000 J of work by exerting a force of 8,000 N. Calculate the displacement in the direction of force.
Solution: Given W = 64,000 J; F = 8,000 N
Work done is given by W = Fs
or 64000 = 8000 × s
or s = 8 m
Example 8: A horse applying a force of 800 N in pulling a cart with a constant speed of 20 m/s. Calculate the power at which horse is working.
Solution: Power, P is given by force × velocity, i.e.
P = F . v
Here F = 800 N; v = 20 m/s
∴ P = 800 × 20 = 16000 watt
= 16 kW
Example 9: A boy keeps on his palm a mass of 0.5 kg. He lifts the palm vertically by a distance of 0.5 m. Calculate the amount of work done.
Use g = 9.8 m/s2.
Solution: Work done, W = F . s
Here, force F of gravity applied to lift the mass, is given by
F = mg
= (0.5 kg) × (9.8 m/s2)
= 4.9 N
and s = 0.5 m
Therefore, W = (4.9) . (0.5m) = 2.45 J.
Example 10: A truck of mass 2500 kg is stopped by a force of 1000 N. It stops at a distance of 320 m. What is the amount of work done ? Is the work done by the force or against the force?
Solution: Here the force, F = 1000 N
Displacement, s = 320 m
∴ Work done, W = F . s
= (1000N) . (320 m)
= 320000 J
In this case, the force acts opposite to the direction of displacement. So the work is done against the force.
Example 11: A car weighing 1200 kg and travelling at a speed of 20 m/s stops at a distance of 40 m retarding uniformly. Calculate the force exerted by the brakes. Also calculate the work done by the brakes.
Solution: In order to calculate the force applied by the brakes, we first calculate the retardation.
Initial speed, u = 20 m/s; final speed,
v = 0, distance covered, s = 90 m
Using the equation, v2 = u2 + 2as, we get
02 = (20)2 + 2 × a × 40
or 80a = –400
or a = –5 m/s2
Force exerted by the brakes is given by
F = ma
Here m = 1200 kg; a = – 5 m/s2
∴ F = 1200 × (–5) = – 6000 N
The negative sign shows that it is a retarding force.
Now, the work done by the brakes is given by
W = Fs
Here F = 6000 N; s = 40 m
∴ W = 6000 × 40 J = 240000 J
= 2.4 × 105 J
∴ Work done by the brakes = 2.4 × 105 J
Example 12. A worker uses a horizontal force of 400 N to push a rubbish cart.
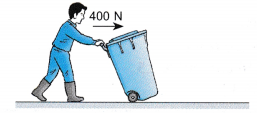
Calculate the work done to push the cart a distance of 180 m on a horizontal surface.
Solution:
Since the direction of the movement of the cart is the same as the direction of the applied force, therefore W = F x s
= 400 x 180 = 72 000 J
Example 13. A boy uses a force of 120 N to pull a crate along a straight corridor. The applied force is at an angle of 30° with the horizontal floor.
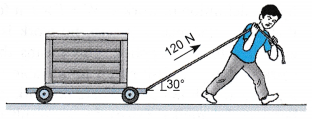
Calculate the work done by him after pulling the crate a distance of 90 m.
Solution:
W = F cos θ x s
= (120 cos 30°) x 90 = 9353 J
Example 14. Jin uses a force of 16 N to mop a floor. The applied force makes an angle of 28° with the floor.
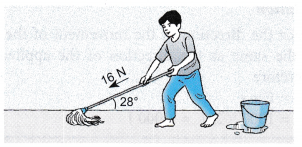
What is the work done by Jin when he pushes the mop a horizontal distance of 2.5 m?
Solution:
W = F cos θ x s
= (16 cos 28°) x 2.5 = 35.3 J