What Is Potential Energy
Potential Energy: Thus the energy possessed by a body by virtue of its position or change in shape is known as potential energy. It is obvious that a body may possess energy even when it is not in motion.
Expression for Potential Energy:
- Gravitational potential energy is the energy of an object because of its higher position in the gravitational field.
- Figure shows a crane lifting an object. Work is done to lift the object. The object gains an amount of energy that equals to the work done to lift it.
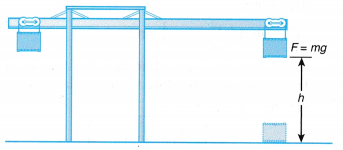
- The downward force is equal to the weight of the object, W = mg.
- Therefore the force, F needed to lift the box at a uniform velocity is equal to mg.
Displacement, s = h
Work done, W = F x s = mgh - Since the work done is transferred to the object as gravitational potential energy, the formula for gravitational potential energy, E is given by:
Ep = mgh
Inter conversion of Potential Energy and Kinetic Energy
Mechanical Energy of a Freely Falling Body:
Assume, a body of mass m is at rest at a height h from the earth’s surface, as it starts falling, its velocity after travelling a distance x (point B) becomes v and its velocity on the earth’s surface is v’.
Mechanical energy of the body at point A:
EA = Kinetic energy + Potential energy
EA = m(0)2 + mgh
EA = mgh ……… (i)
Mechanical energy of the body at point B:
EB = \(\frac { 1 }{ 2 }\) mv2 + mg (h – x) ……..(ii)
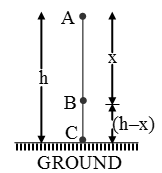
Mechanical energy of the body at point C:
EC = \(\frac { 1 }{ 2 }\) m (v’)2 + mg × 0
EC = \(\frac { 1 }{ 2 }\) m (v’)2 ……..(iv)
Use: EA = EB = EC
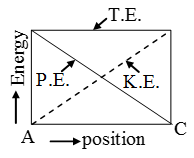
Hence, when a body falls freely, its mechanical energy will be constant. That means, the total energy of the body during free fall, remains constant at all positions. However, the form of energy keeps on changing at all points during the motion.
Potential Energy Example Problems With Solutions
Example 1. What will be the potential energy of a body of mass 2 kg kept at a height of 10 m ?
Solution: The potential energy is given by
U = mgh
Here, m = 2 kg; g = 10 m/s2; h = 10 m
∴ U = 2 × 10 × 10 = 200 J
Example 2. In lifting a mass of 25 kg to a certain height 1250 J energy is utilized. Calculate to what height it has been lifted ? (Take g = 10 m/s2)
Solution: In lifting a mass through a height h the work done is given by
U = mgh
Here, U = 1250 J; g = 10 m/s2; m = 25 kg
∴ 1250 = 25 × 10 × h
or h = 5 m
Example 3. During a physical exercise, Samad, with a mass of 75 kg, is lifted to a height of 2.1 m. Idris, with a mass of 46 kg, is lifted to a height of 3.2 m.
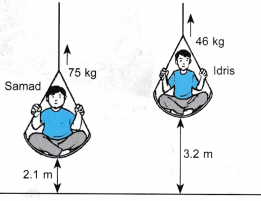
Which of the two boys has gained more gravitational potential energy? [g = 9.8 m s-2]
Solution:
For Samad;
Gravitational potential energy,
Ep = 75 x 9.8 x 2.1
= 1543.5 J
For Idris;
Gravitational potential energy,
Ep = 46 x 9.8 x 3.2 P
= 1442.6 J
Therefore, Samad has gained more gravitational potential energy.
Example 4. A lift with its passengers has a total mass of 1350 kg. Calculate the gravitational potential energy gained by the lift by moving upwards to a height of 25 m. [g = 9.8 m s-2J]
Solution:
Mass, m = 1350 kg; Height, h = 25 m Therefore,
Gravitational potential energy,
Ep = mgh
= 1350 x 9.8 x 25 = 330 750 J