What is Motion
When a body does not change its position with time, we can say that the body is at rest, while if a body changes its position with time, it is said to be in motion.
Analysing Linear Motion
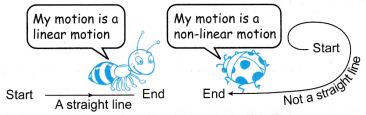
- Linear motion is motion in a straight line.
- Non-linear motion is motion that is not in a straight line.
- When analysing linear and non-linear motion, distance, displacement, speed, velocity, acceleration and deceleration are some commonly encountered physical quantities.
Terms Used To Define Motion
An object is said to be a point object if it changes its position by distances which are much greater than its size. A point or some stationary object with respect to which a body continuously changes its position in the state of motion is known as origin or reference point.
When we say an object is moving, it is always with respect to another object. For example, when we say a vehicle is moving on a road, it is moving with respect to the trees and poles on the road, which are ‘not moving’. When you say you are at rest or not moving while reading a book, it is with respect to your chair or your desk. When an object moves, its position (with respect to another object) changes with time. Let us take the example of a car moving away from a building.

When the car is at position A, the distance between the car and the building is very small. As the car moves away from the building (Position B), its distance from the building increases. Another way of saying this is that when the car moves, its position with respect to the building changes with time. An object is said to be in motion if its position (with respect to another object) changes with time.
Types Of Motion
There are different types of motion: translational, rotational, periodic, and non periodic motion.
Translational Motion
A type of motion in which all parts of an object move the same distance in a given time is called translational motion. Examples are vehicles moving on a road, a child going down a bird flying in the sky. Translational motion can be of two types, rectilinear and curvilinear. Table shows the differences between rectilinear and curvilinear motions.
| Rectilinear motion | Curvilinear motion |
| 1. When an object in translational motion moves in a straight line, it is said to be in rectilinear motion. | 1. When an object in translational motion moves along a curved path, it is said to be in curvilinear motion. |
| 2. Examples are a car moving on a straight road and a train moving on a straight track. | 2. Examples are a stone thrown up in the air at an angle and a car taking a turn. |
 Examples of translational motion: a child going down a slide.
Examples of translational motion: a child going down a slide.
Rotational Motion
When an object moves about an axis and different parts of it move by different distances in a given interval of time, it is said to be in rotational motion. Examples of objects undergoing rotational motion are blades of a rotating fan, merry-go-round, blades of a windmill. When an object undergoes rotational motion, all its parts do not move the same distance in a given interval of time. For example, the outer portion of the blades of a windmill moves much more than the portion closer to the centre.
A merry-go-around shows rotational motion:

Periodic Motion
A type of motion that repeats itself after equal intervals of time is called periodic motion. Examples of objects undergoing periodic motion are the to and fro motion of a pendulum, the Earth (rotating on its axis), the hands of a clock, the blades of a rotating electric fan, and the plucked string of a guitar.

Non-periodic Motion
A motion that does not repeat itself at regular intervals or a motion that does not repeat itself at all is called non-periodic motion. Examples of non-periodic motion are a car moving on a road, a bird gliding across the sky, and children playing in a park. In everyday life, we observe more than one type of motion, like
- Birds gliding across the sky (translational and non periodic).
- Rotation of the Earth on its axis (rotational and periodic).

According to Directions
- One dimensional motion is the motion of a particle moving along a straight line.
- Two dimensional motion A particle moving along a curved path in a plane has
2-dimensional motion. - Three dimensional motion Particle moving randomly in space has 3-dimensional motion.
According to State of Motion
- Uniform Motion: A body is said to be in a state of uniform motion if it travels equal distances in equal intervals of time. If the time distance graph is a straight line the motion is said to be uniform motion.
- Non-uniform motion: A body has a non-uniform motion if it travels unequal distances in equal intervals of time. Ex. a freely falling body.
Time – distance graph for a body with non-uniform motion is a curved line.
Analysing Motion Graphs
 Displacement- Time graphs:
Displacement- Time graphs:
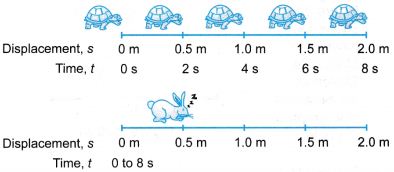
- Figure shows a tortoise moving at a slow and steady speed while a hare was sleeping soundly from the time t = 0 to 8 s.
- We can represent the situation using displacement-time graphs.
(a) The graph in Figure (a) shows the displacement of the tortoise from the starting line from time t = 0 to 8 s.
(b) The graph in Figure (b) shows that throughout the time from t = 0 to 8 s, the hare had a displacement of 0.5 m from the starting line. Throughout the 8 seconds, it did not move at all as it was sleeping.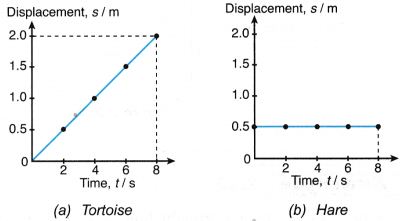
- The gradient of the s-t graph of an object gives the rate of change of displacement, which is the velocity of the object.
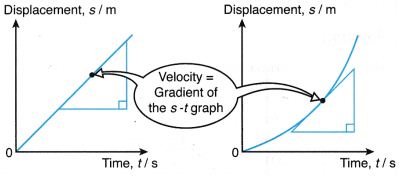
- Table illustrates some of the displacement-time graphs.
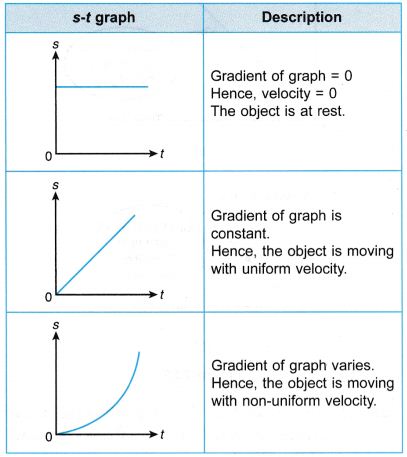
The straight line inclined to time axis in s-t graph represents constant velocity.
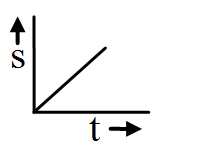
In s-t graph the straight line inclined to time axis at angle greater than 90º shows negative velocity
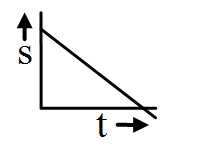
Body with accelerated motion
Body with decelerated motion
Velocity -Time graphs:
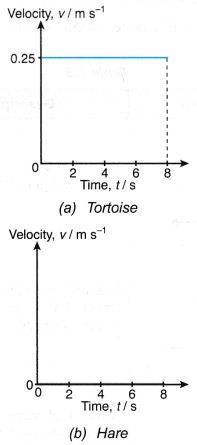
- The gradients of the s-t graphs for the tortoise and hare are 0.25 m s-1 and 0 m s-1 respectively.
- The v-t graphs in Figure represent the situation.
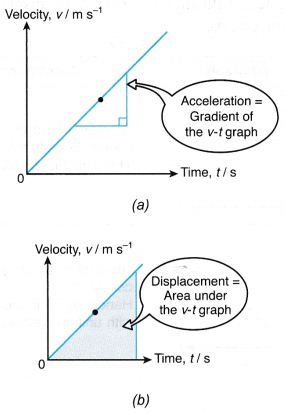
(a) The gradient of the v-t graph is the rate of change of velocity which is the acceleration of the object.
(b) The area under the graph gives the displacement of the object. - Table illustrates some of the velocity-time graphs.

For the body having constant velocity or zero acceleration.
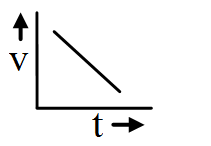
The body is moving with constant retardation and its initial velocity is not zero.
The body is accelerated and the initial velocity is zero.
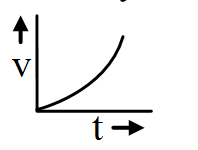
The body is decelerated
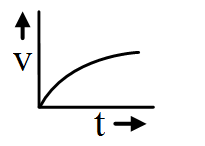
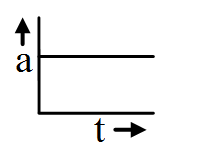
Acceleration-Time graph:
Acceleration is constant
Acceleration is increasing and is +ve
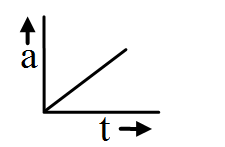
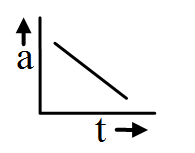
Acceleration is decreasing and is –ve
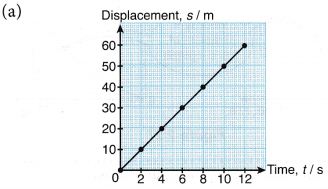
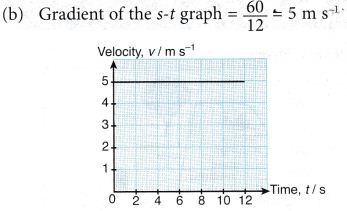
Example 1. A boy skated along a straight line passing by two points, P and Q. His time, t and displacement, s from point P is shown in Figure.
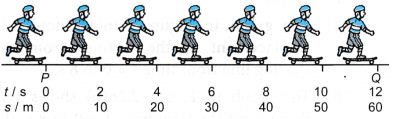
From the information given, draw the
(a) s-t graph
(b) v-t graph
Solution:
Example 2. Azlan cycled along a straight road. The graph in Figure (b) illustrates his motion.

(a) Calculate the velocity of Azlan from t = 0 to 10 s.
(b) Describe what happened to Azlan from t = 10 to 20 s.
(c) Calculate the displacement, s of Azlan when t = 25 s.
(d) Where was Azlan when t = 35 s?
Solution:
(a) Refer to part AB of the graph.
Velocity = Gradient of the graph
= 50/10 = 5 m s-1
(b) Refer to part BC of the graph. The gradient of the graph is 0. This means that Azlan was at rest from t = 10 to 20 s.
(c) Refer to point D of the graph. When
t = 25 s, displacement of Azlan, s = 14 m.
(d) Refer to point E of the graph. When
t = 35 s, displacement of Azlan, s = 0 m.
This means that Azlan was back at the starting position.
Example 3. Figure shows a huge crane hoisting a steel beam from the ground. The v-t graph shows the motion of the beam in the first 9 s.
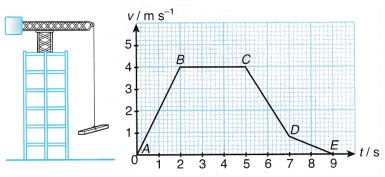
(a) Briefly describe the motion of the beam represented by AB, BC, CD and DE.
(b) Calculate the initial and final acceleration of the beam.
(c) Calculate the height of the beam from the ground after 9 seconds.
Solution:

Example 4. The v-t graph in Figure shows the motion of a mine cart on a straight railway.
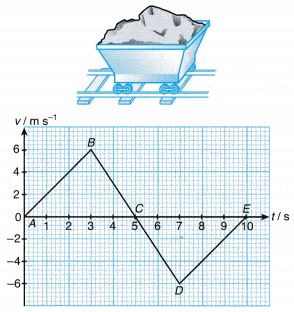
(a) What was the total distance travelled by the mine cart?
(b) (i) Where was the mine cart when t = 10 s?
(ii) Explain your answer in (b) (i).
Solution:
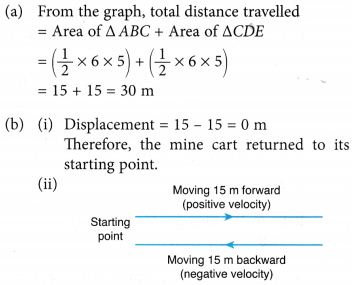
From t = 0 s to 5 s, the mine cart moved 15 m forward (positive velocity).
From t = 5 to 10 s, the mine cart moved 15 m backward (negative velocity).
Hence, the mine cart returned to its starting point.