Lens Formula & Magnification – Lens Power

Numerical Methods In Lens

(A) Lens Formula  

• Definition: The equation relating the object distance (u), the image distance (v) and the focal length (f) of the lens is called the lens formula.
  Assumptions made:
  1. The lens is thin.
  2. The lens has a small aperture.
  3.  The object lies close to principal axis.
  4. The incident rays make small angles with the lens surface or the principal axis.
• When a lens of known focal length, f is used to find the relationship between the object distance,
  u and the image distance v, the value of (1/u + 1/v) is a constant.
• This constant value is equal to 1/f.
  Therefore, the relationship between the object distance, the image distance and the focal length of a lens is given by the
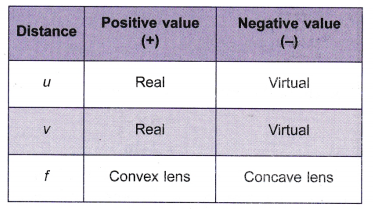
  \( \text{Lens Formula:   }\frac{1}{u}+\frac{1}{v}=\frac{1}{f} \)
• The lens formula may be applied to convex lenses as well as concave lenses provided the ‘real is positive’ sign convention is followed.
• Table shows the sign convention for the values of object distance, image distance and focal length. All distances are measured from the optical centre of the lens.
  

People also ask

• What is a Lens?
• What are the Types of Spherical Lenses
• Image Formation By Concave And Convex Lenses
• The Uses of Lenses in Optical Devices
• To Construct Optical Devices Using Lenses

(B) Linear Magnification For Lens

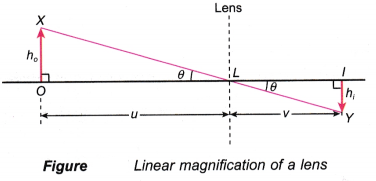
Definition: The ratio of the size of the image formed by refraction from the lens to the size of the object, is called linear magnification produced by the lens. It is represented by the symbol m.

• • The size of an image formed by a lens varies with the position of the object.
  • The simplest way to compare the image with the object is by the ratio of their sizes. This ratio is the linear magnification.
    

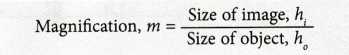
• The ratio of the image size to the object size is the same as the ratio of the image distance to the object distance.
  
• In symbols,
  

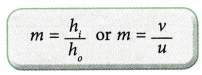
(C) Power Of Lens

Definition: It is the capacity or the ability of a lens to deviate (converge or diverge) the path of rays passing through it.

• A lens producing more converging or more diverging, is said to have more power.
• The power of a lens is related to its focal length, f by the equation:
  \( \text{Power of lens }\left( \text{in diopter} \right)\propto \frac{1}{\text{f (in}\,\,\text{metre)}}\)
  
• The unit for power is dioptre (D).
• The shorter the focal length, the greater the power.
• The power for a convex lens is positive and the power for a concave lens is negative.

Lens Equation Problems and Solutions

1. Figure shows a graph of v against u.
   
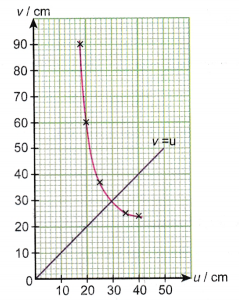
   Determine the focal length of the lens.
   Solution:
   
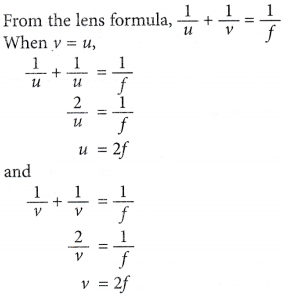
   From the graph, when v = u, the coordinate of the point of intersection is given as (2f, 2f), where f is the focal length of the lens.
   2f = 30
   f = 15 cm
   The focal length of the lens is 15 cm.
2. Figure shows a graph of v against magnification, m for a lens experiment.
   
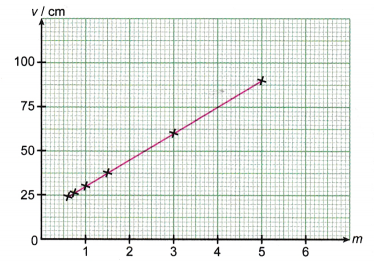
   What is the focal length of the lens used in the experiment?
   Solution:
   
   This is the general equation for the straight line in a graph of v against m. From the graph, the focal length of the lens is 15 cm (Gradient of graph or intercept at v-axis).
3. An object is placed in front of a convex lens with a focal length, f of 10 cm. What are the characteristics of the image formed if the object distance is 15 cm?
   Solution:
   Object distance, u = +15 cm (real object);
   Focal length, f = +10 cm (convex lens);
   
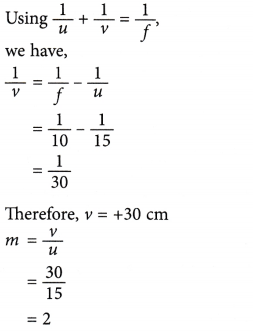
   Therefore, the image is real, inverted, 30 cm from the lens, on the opposite side of the object and magnified 2 times.
4. An object of height 6 cm is placed at a distance of 20 cm from a concave lens. Its focal length is 10 cm. Find the position and size of the image.
   Solution:
   
   The image is virtual, at a distance of 6.7 cm from the lens on the same side as the object and has a height of 2 cm.
5. Figure shows the position of an image, I of an object, O formed by a convex lens. The height of the object, ho is 5 cm.
   
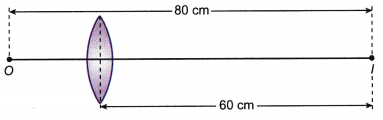
   What is the height of the image, h_o ?
   Solution:
   
   

Focal Length of Convex Lens Experiment

Aim: To find the relationship between the object distance, u, image distance, v and the focal length, f of a lens.
Apparatus: Light bulb, convex lens (f = 15 cm), metre rule, white screen, lens holder
Method:

1. The apparatus is set up as shown in figure.
2. The light bulb is kept at a fixed position at one end of the metre rule. The convex lens is moved to a position where the object distance, u = 40 cm. The bulb is switched on and the screen is moved backward and forward to get a sharp image formed on it. The image distance, v is measured and recorded.
3. Step 2 is repeated for object distances, u = 35 cm, 30 cm, 25 cm, 20 cm and 18 cm. All the corresponding values of the image distance, v are measured and recorded. The results are tabulated in Table.
4. The values of 1/u, 1/v and (1/u + 1/v) are calculated and corrected to two significant figures. The mean value for (1/u + 1/v) is determined.
5. The focal length, f of the convex lens used in the activity is given as 15 cm. The value of 1/f is determined
   11 ‘ and this value is compared with the mean value of (1/u + 1/v).

Results:

1. The focal length of the lens used, f = 15 cm.
2. Tabulation of results.
   
3. The mean value for (1/u + 1/v) is 0.067.
   The focal length, f = 15 cm, the reciprocal, = 1/f = 0.067 cm^-1

Discussion:

1. If a graph of 1/v against 1/u is plotted, the graph is as shown in Figure.
   
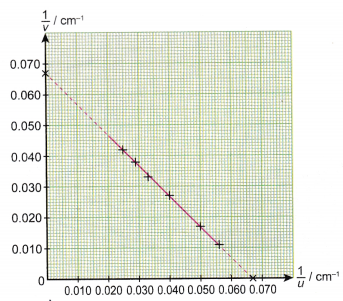
2. The graph is a straight line graph cutting the two axes at two intercepts. The values of the intercepts are both equal to 0.067.
3. From the graph,
   

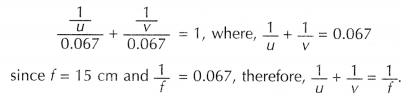
Conclusion:
The relationship between the object distance, u, image distance, v and focal length, f of a lens is