How To Calculate The Area Of A Circle

How To Calculate The Area Of A Circle

A circle is the locus of a point which moves in a plane in such a way that its distance from a fixed point always remains same.
The fixed point is called the centre and the given constant distance is known as the radius of the circle.
The perimeter of a circle is known as its circumference.
If r is the radius of a circle, then
(i) Circumference = 2πr or πd, where d = 2r is the diameter of the circle.
(ii) Area = πr² or πd²/4
(iii) Area of semi-circle = πr²/2
(iv) Area of a quadrant of a circle = πr²/4

Read More:

• Parts of a Circle
• Perimeter of A Circle
• Common Chord of Two Intersecting Circles
• Construction of a Circle
• Properties of Circles
• Sector of A Circle
• The Area of A Segment of A Circle
• The Area of A Sector of A Circle

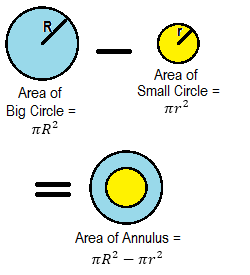
Area Enclosed By Two Concentric Circles

If R and r are radii of two con-centric circles, then
area enclosed by the two circles = πR² – πr² = π(R² – r²) = π(R + r) (R – r)

Some useful results:
(i) If two circles touch internally, then the distance between their centres is equal to the difference of their radii.
(ii) If two circles touch externally, then the distance between their centres is equal to the sum of their radii.
(iii) Distance moved by a rotating wheel in one revolution is equal to the circumference of the wheel.
(iv) The number of revolutions completed by a rotating wheel in one minute
\(\frac{\text{Distance moved in one minute}}{\text{Circumference}} \)

Area Of A Circle With Examples

Example 1:    Find the area of a circle whose circumference is 22 cm.
Sol.    Let r be the radius of the circle. Then,
Circumference = 22 cm
⇒ 2πr = 22
⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 22
⇒ r = \(\frac { 7 }{ 2 }\) cm
therefore Area of the circle = πr² = \(\frac { 22 }{ 7 }\) × 7²
= 38.5 cm²

Example 2:    Find the area of a quadrant of a circle whose circumference is 22 cm.
Sol.    Let r be the radius of the circle. Then,
Circumference = 22 cm
⇒  2πr = 22
⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 22
⇒ r = \(\frac { 7 }{ 2 }\) cm
∴ Area of a quadrant = \(\frac { 1 }{ 4 }\) πr²
=  \(\frac { 77 }{ 4 }\) = 9.625 cm²

Example 3:    Two circles touch externally. The sum of their areas is 130 sq. cm. and the distance between their centres is 14 cm. Find the radii of the circles.
Sol.    If two circles touch externally, then the distance between their centres is equal to the sum of their radii.

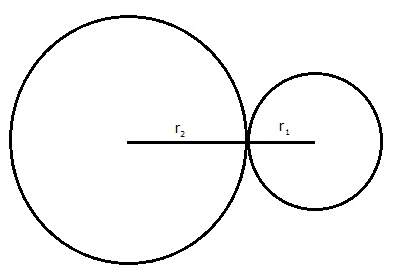
Let the raddi of the two circles be r₁ cm and r₂ cm respectively.
Let C₁ and C₂ be the centres of the given circles. Then,
C₁C₂ = r₁ + r₂
⇒ 14 = r₁ + r₂       [∵ C₁C₂ = 14 cm (given)]
⇒ r₁ + r₂ = 14           ….(i)
It is given that the sum of the areas of two circles is equal to 130 cm².
∴ πr₁²+ πr₂² = 130π
⇒ r₁² r₂² + r₂²= 130         ….(ii)
Now,
(r₁ + r₂)² = r₁² + r₂² + 2r₁r₂
⇒ 14² = 130 + 2r₁r₂         [Using (i) and (ii)]
⇒ 196 – 130 = 2r₁r₂
⇒ r₁ r₂ = 33        ….(iii)
Now,
(r₁ – r₂)² = r₁² + r₂² – 2r₁r₂
⇒ (r₁ – r₂)² = 130 – 2 × 33          [Using (ii) and (iii)]
⇒ (r₁ – r₂)² = 64   ⇒   r₁ – r₂ = 8         ….(iv)
Solving (i) and (iv), we get r₁ = 11 cm and r₂ = 3 cm.
Hence, the radii of the two circles are 11 cm and 3 cm.

Example 4:    Two circles touch internally. The sum of their areas is 116 π cm² and distance between their centres is 6 cm. Find the radii of the circles.
Sol.    Let R and r be the radii of the circles having centres at O and O’ respectively. Then,

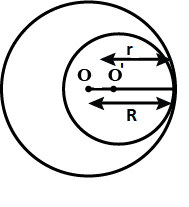
Sum of areas = 116π cm²
⇒ πR² + πr² = 116 π
⇒ R² + r² = 116 ….(i)
Distance between the centres = 6 cm
⇒ OO’ = 6 cm
⇒ R – r = 6 ….(ii)
Now, (R + r)² + (R – r)² = 2(R² + r²)
⇒ (R + r)² + 36 = 2 × 116        [Using (i) and (ii)]
⇒ (R + r)² = (2 × 116 – 36) = 196
⇒ R + r = 14         …..(iii)
Solving (ii) and (iii), we get R = 10 and r = 4.
Hence, radii of the given circles are 10 cm and 4 cm respectively.

Example 5:    A copper wire, when bent in the form of a square, encloses an area of 484 cm2. If the same wire is bent in the form of a circle, find the area enclosed by it (Use π = \(\frac { 22 }{ 7 }\) ).
Sol.    We have,
Area of the square = √484 cm²
∴ Side of the square √484 cm = 22 cm       \( \left[ \because \text{ }\,\,\text{Area = (Side}{{\text{)}}^{\text{2}}}\text{ }\Rightarrow \text{ Side = }\sqrt{\text{Area}} \right] \)
So, Perimeter of the square = 4 (side)
= (4 × 22) cm = 88 cm
Let r be the radius of the circle. Then,
Circumference of the circle = Perimeter of the square.
⇒ 2πr = 88
⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 88
⇒ r = 14 cm
∴ Area of the circle = πr²
\( \text{=}\left\{ \frac{\text{22}}{\text{7}}\text{ }\!\!\times\!\!\text{ (14}{{\text{)}}^{\text{2}}} \right\}\text{ c}{{\text{m}}^{\text{2}}} \)
= 616 cm²

Example 6:    Fig. depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue, Black and white. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
Sol.    We have,

r = Radius of the region representing Gold score = 10.5 cm
∴ r₁ = Radius of the region representing Gold and Red scoring areas
= (10.5 + 10.5) cm = 21 cm = 2r cm
r₂ = Radius of the region representing Gold, Red and Blue scoring areas
= (21 + 10.5) cm = 31.5 cm = 3r cm
r₃ = Radius of the region representing Gold, Red, Blue and Black scoring areas
= (31.5 + 10.5) cm = 42 cm = 4r cm
r₄ = Radius of the region representing Gold, Red, Blue, Black and white scoring areas
= (42 + 10.5) cm = 52.5 cm = 5r cm
Now, A₁ = Area of the region representing Gold scoring area
= πr² = 22/7× (10.5)² = 22/7 × 10.5 × 10.5
= 22 × 1.5 × 10.5 = 346.5 cm²
A₂ = Area of the region representing Red scoring area
= π(2r)² – πr² = 3πr² = 3A₁ = 3 × 346.5 cm²
= 1039.5 cm²
A₃ = Area of the region representing Blue scoring area
= π (3r)² – π(2r)² = 9πr² – 4πr² = 5πr² = 5A₁
= 5 × 346.5 cm² = 1732.5 cm²
A₄ = Area of the region representing Black scoring area
= π (4r)² – π(3r)² = 7πr²
= 7 A₁ = 7 × 346.5 cm² = 2425.5 cm²
A₅ = Area of the region representing White scoring area
= π(5r)² – π(4r)² = 9πr²
= 9 A₁ = 9 × 346.5 cm² = 3118.5 cm²