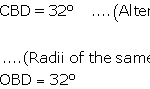Selina Concise Mathematics Class 10 ICSE Solutions Constructions (Circles)Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 19 Constructions (Circles)Constructions Circles Exercise 19 – Selina Concise Mathematics Class 10 ICSE Solutio…

Selina Concise Mathematics Class 10 ICSE Solutions CirclesSelina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 17 CirclesCircles Exercise 17A – Selina Concise Mathematics Class 10 ICSE SolutionsCircles Class 10 Question 1. In the given f…

ICSE Solutions for Class 10 Mathematics – CirclesICSE SolutionsSelina ICSE SolutionsGet ICSE Solutions for Class 10 Mathematics Chapter 15 Circles for ICSE Board Examinations on APlusTopper.com. We provide step by step Solutions for ICSE Mathematics Clas…

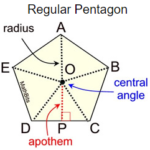
Area of Polygons and CirclesArea formulas can be found at “Reference Table for Areas” Let’s pick up some hints for those more challenging problems involving area.Regular polygons have a center and a radius (coinciding with their circumscribed circle), an…

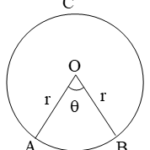
How To Find The Area Of A Sector Of A Circle If the arc subtends an angle of θ at the centre, then its arc length is \( \frac{\text{ }\!\!\theta\!\!\text{ }}{\text{180}}\text{ }\!\!\times\!\!\text{ }\!\!\pi\!\!\text{ r} \) Hence, the arc length ‘l’ of a…

Perimeter Of A CircleCircumference of a CircleCircumference means, ‘the perimeter of a circle’. The word has been derived from the Latin word circumferre means to carry around. The distance around a circular region is also known as its circumference. N…

How To Find The Area Of A Segment Of A CircleArea of the sector OPRQ = Area of the segment PRQ + Area of ∆OPQ ⇒  Area of  segment PRQ = \(\left\{ \frac{\pi }{360}\times \theta -\sin \frac{\theta }{2}\cos \frac{\theta }{2} \right\}{{r}^{2}} \)Read More:…

 What Is Segment Of A CircleSegment of a circle: The region enclosed by an arc and a chord is called the segment of the circle. Minor segment: If the boundary of a segment is a minor arc of a circle, then the corresponding segment is called a minor segm…

What Is Sector Of A Circle Minor sector: A sector of a circle is called a minor sector if the minor arc of the circle is a part of its boundary In Fig. sector OAB is the minor sector. Major sector: A sector of a circle is called a major sector if the ma…

What Are The Properties Of CirclesTwo circles are congruent, if and only if they have equal radii. Two arcs of a circle are congruent if the angles subtended by them at the centre are equal. Two arcs subtend equal angles at the centre, if the arcs are c…