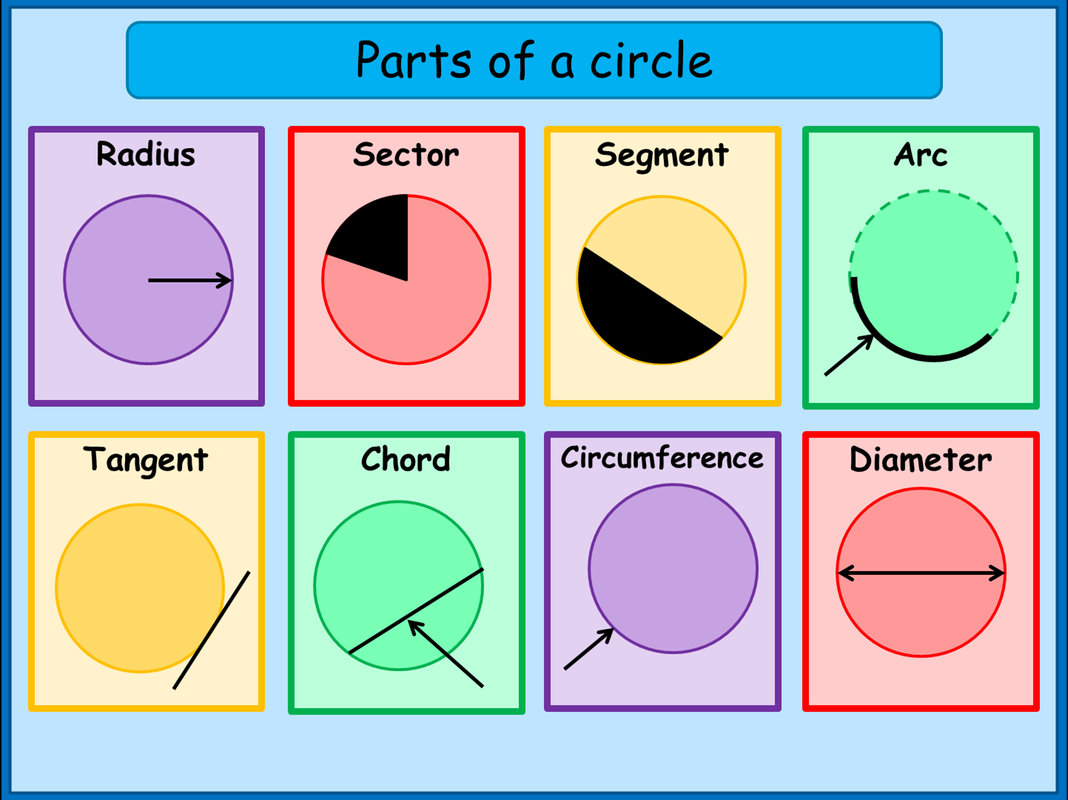
What are the Parts of a Circle
So far, we have discussed about the triangle and quadrilateral that have linear boundaries. Circle is a closed figure that has a curvilinear boundary.
 When we think of circles, the very first thing that comes to our mind is its round shape, for example, bangles, coins, rings, plates, chapattis, pizzas, CDs etc. Wheels of a car, bus, cycle, truck, train, and aeroplane are also round in shape. If we take a stone, tie it to one end of a string and swing it in the air by holding the other end of the string, the path traced by the stone will be a circular path and it will make a circle.
When we think of circles, the very first thing that comes to our mind is its round shape, for example, bangles, coins, rings, plates, chapattis, pizzas, CDs etc. Wheels of a car, bus, cycle, truck, train, and aeroplane are also round in shape. If we take a stone, tie it to one end of a string and swing it in the air by holding the other end of the string, the path traced by the stone will be a circular path and it will make a circle.
Read More:
- Perimeter of A Circle
- Common Chord of Two Intersecting Circles
- Construction of a Circle
- The Area of A Circle
- Properties of Circles
- Sector of A Circle
- The Area of A Segment of A Circle
- The Area of A Sector of A Circle
- Classification of triangles
- Circle: A circle is a collection of all those points in a plane that are at a given constant distance from a given fixed point in the plane.
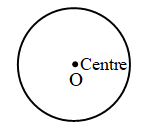
- Centre: Circle is a closed figure made up of points in a plane that are at the same distance from a fixed point, called the centre of the circle. In the figure O is the centre.
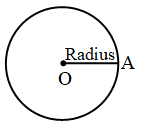
- Radius: The constant distance from its centre is called the radius of the circle. In the figure, OA is radius
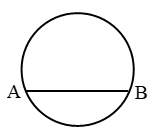
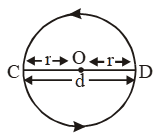
- Chord: A line segment joining two points on a circle is called a chord of the circle. In the figure, AB is a chord of the circle. If a chord passes through centre then it is longest chord. PQ, PR, and ST are chords of the circle. Chord ST passes through the centre, hence it is a diameter.
- Diameter: A chord passing through the centre of a circle is called the diameter of the circle. A circle has an infinite number of diameters. CD is the diameter of the circle as shown in the figure. If d is the diameter of the circle then d = 2r. where r is the radius. or the longest chord is called diameter.
In the figure, AB is the diameter and the arcs CD and DC are semicircles.
- Arc: A continuous piece of a circle is called an arc. Let A,B,C,D,E,F be the points on the circle. The circle is divided into different pieces. Then, the pieces AB, BC, CD, DE, EF etc. are all arcs of the circle.
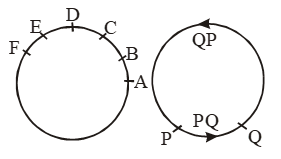 Let P,Q be two points on the circle. These P, Q divide the circle into two parts. Each part is an arc. These arcs are denoted in anti-clockwise direction
Let P,Q be two points on the circle. These P, Q divide the circle into two parts. Each part is an arc. These arcs are denoted in anti-clockwise direction

- Circumference of a circle: The perimeter of a circle is called its circumference. The circumference of a circle of radius r is 2πr.
- Semicircle: The diameter of a circle divides the circle into two equal parts. Each part is called a semi-circle. We can also say that half of a circle is called a semi¬circle. In the figure, AXB and AYB represents two semi-circles.
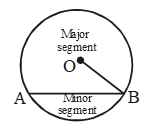
- Segment: Let AB be a chord of the circle. Then, AB divides the region enclosed by the circle (i.e., the circular disc) into two parts. Each of the parts is called a segment of the circle. The segment, containing the minor arc is called minor segment and the segment, containing the major arc, is called the major segment and segment of a circle is the region between an arc and chord of the circle.
- Central Angles: Consider a circle. The angle subtended by an arc at the centre O is called the central angle. The vertex of the central angle is always at the centre O.
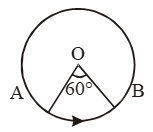
- Degree measure of an arc: Degree measure of a minor arc is the measure of the central angle subtended by the arc.

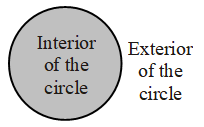
The degree measure of the circumference of the circle is always 360°. - Interior and Exterior of Circle
A circle divides the plane on which lies into three parts.
(i) Inside the circle. which is called the interior of the circle
(ii) Circle
(iii) Outside the circle, which is called the exterior of the circle.
The circle and its interior make up the circular region.
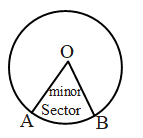
- Sector:
A sector is that region of a circular disc which lies between an arc and the two radii joining the extremities of the arc and the centre. OAB is a sector as shown in the figure.
Quadrant: One fourth of a circular disc is called a quadrant.
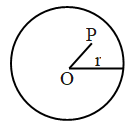
- Position of a point:
Point Inside the circle: A point P, such that OP < r, is said to lie inside the circle.
 The point inside the circle is also called interior point. (Example : Centre of cirle)
The point inside the circle is also called interior point. (Example : Centre of cirle)
Point outside the circle: A point Q, such that OQ > r, is said to lie outside the circle C (O, r) = {X, OX = r}
The point outside the circle is also called exterior point.
Point on the circle: A point S, such that OS = r is said to lie on the circle C(O, r) = {X ,OX = r}.
Circular Disc: It is defined as a set of interior points and points on the circle. In set notation, it is written as : C(O, r) = {X : P OX ≤ r}
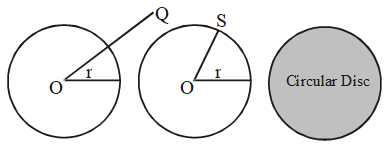
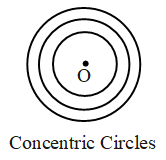
- Concentric Circles:
Circles having the same centre and different radius are said to be concentric circles.
Remark. The word ‘radius’ is used for a line segment joining the centre to any point on the circle and also for its length.
- Congruence of Circles & Arcs
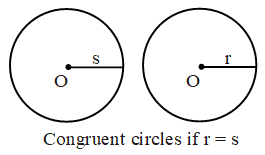
Congruent circles: Two circles are said to be congruent if and only if, one of them can be superposed on the other, so as the cover it exactly. It means two circles are congruent if and only if, their radii are equal. i.e., C (O, r) and C (O’ , r) are congruent if only if r = s.
 Congruent arcs: Two arcs of a circle are congruent, if either of them can be superposed on the other, so as to cover it exactly. It is only possible, if degree measure of two arcs are the same.
Congruent arcs: Two arcs of a circle are congruent, if either of them can be superposed on the other, so as to cover it exactly. It is only possible, if degree measure of two arcs are the same.
Example 1: Take two points A and B on a plane sheet. Draw a circle with A as a centre, AC as radius and B in its exterior.
Solution: Mark two points A and B on a paper.
A • • B
As the point B should be in the exterior of the circle, take A as the centre and radius (r) less than AB to draw a circle.

Example 2 :Find the diameter of the circle of radius 6 cm.
Solution: We know,
Diameter = 2 × radius
∴ Diameter =2 × 6 cm =12 cm