How Many Types Of Quadrilaterals Are There
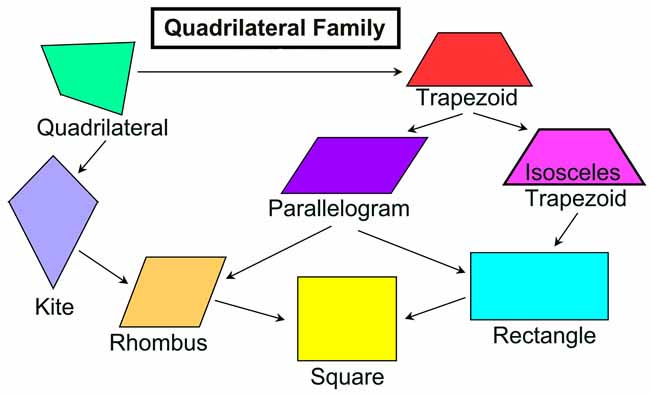
- A quadrilateral is a figure bounded by four line segments such that no three of them are parallel.
- Two sides of quadrilateral are consecutive or adjacent sides, if they have a common point (vertex).
- Two sides of a quadrilateral are opposite sides, if they have no common end-point (vertex).
- The consecutive angles of a quadrilateral are two angles which include a side in their intersection.
- In other words, two angles are consecutive, if they have a common arm.
- Two angles of a quadrilateral are said to be opposite angles if they do not have a common arm.
- The sum of the four angles of a quadrilateral is 360º.
- A quadrilateral having exactly one pair of parallel sides, is called a trapezium.
- A trapezium is said to be an isoscels trapezium, if its non-parallel sides are equal.
- A quadrilateral is a parallelogram if its both pairs of opposite sides are parallel.
- A parallelogram having all sides equal is called a rhombus.
- A parallelogram whose each angle is a right angle, is called a rectangle.
- A square is a rectangle with a pair of adjacent sides equal.
- A quadrilateral is a kite if it has two pairs of equal adjacent sides and unequal opposite sides.
- A diagonal of a parallelogram divides it into two congruent triangles.
- In a parallelogram, opposite sides are equal.
- The opposite angles of a parallelogram are equal.
- The diagonals of a parallelogram bisect each other.
- In a parallelogram, the bisectors of any two consecutive angles intersect at right angle.
- If diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle.
- The angle bisectors of a parallegram form a rectangle.
- A quadrilateral is a parallelogam if its opposite sides are equal.
- A quadrilateral is a parallelogram if its opposite angles are equal.
- If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
- A quadrilateral is a parallelogram, if its one pair of opposite sides are equal and parallel.
- Each of the four angles of a rectangel is a right angle.
- Each of the four sides of a rhombus is of the same length.
- Each of the angles of a square is a right angle and each of the four sides is of the same length.
- The diagonals of a rectangle are of equal length.
- If the two diagonals of parallelogram are equal, it is a rectangle.
- The diagonals of a rhombus are perpendicular to each other.
- If the diagonals of a parallelogram are perpendicular, then it is a rhombus.
- The diagonals of a square are equal and perpendicular to each other.
- If the diagonals of a parallelogram are equal and intersect at right angles then the parallelogram is a square.
- A diagonal of a parallelogram divides it into two triangles of equal area.
- For each base of a parallelogram, the corresponding altitude is the line segment from a point on the base, perpendicular to the line containing the opposite side.
- Parallelograms on the same base and between the same parallels are equal in area.
- A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
- The area of a parallelogram is the product of its base and the corresponding altitude.
- Parallelograms on equal bases and between the same parallels are equal in area.
Read More:
- Different Kinds of Quadrilateral
- Properties of Cyclic Quadrilaterals
- RS Aggarwal Class 9 Solutions Quadrilaterals and Parallelograms
Types Of Quadrilaterals Example Problems With Solutions
Example 1: In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 2 : 4 : 5 : 7. Find the measure of each angles of the quadrilateral.
Solution: We have ∠A : ∠B : ∠C : ∠D = 2 : 4 : 5 : 7.
So, let ∠A = 2xº, ∠B = 4xº, ∠C = 5xº, ∠D = 7xº.
∴ ∠A + ∠B + ∠C + ∠D = 360º
⇒ x + 4x + 5x + 7x = 360º
⇒ 18x = 360º
⇒ x = 20º
Thus, the angles are:
∠A = 40º, ∠B = (4 × 20)º = 80º,
∠C = (5 × 20)º = 100º
and, ∠D = (7x)º = (7 × 20)º = 140º
Example 2: The sides BA and DC of a quadrilateral ABCD are produced as shown in fig.
Prove that a + b = x + y.
Solution: Join BD. In ∆ABD, we have

∠ABD + ∠ADB = bº ….(i)
In ∆CBD, we have
∠CBD + ∠CDB = aº ….(ii)
Adding (i) and (ii), we get
(∠ABD + ∠CBD) + (∠ADB + ∠CDB) = aº + bº
⇒ xº + yº = aº + bº
Hence, x + y = a + b
Example 3: In a quadrilateral ABCD, AO and BO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB = 1/2 (∠C + ∠D).
Solution: In ∆AOB, we have

∠AOB + ∠1 + ∠2 = 180º
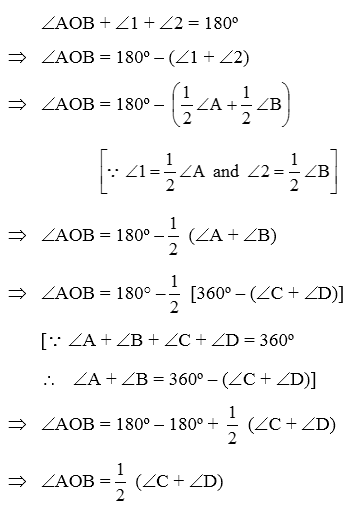
Example 4: In figure bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that
∠P + ∠Q = 1/2 (∠ABC + ∠ADC)

Solution:


Example 5: In a parallelogram ABCD, prove that sum of any two consecutive angles is 180º.
Solution: Since ABCD is a parallelogram. Therefore,
AD || BC.

Now, AD || BC and transversal AB intersects them at A and B respectively.
∴ ∠A + ∠B = 180º
[∵ Sum of the interior angles on the same side of the transversal is 180º]
Similarly, we can prove that
∠B + ∠C = 180º, ∠C + ∠D = 180º and
∠D + ∠A = 180º.
Example 6: In a parallelogram ABCD, ∠D = 115º, determine the measure of ∠A and ∠B.
Solution: Since the sum of any two consecutive angles of a parallelogram is 180º. Therefore,
∠A + ∠D = 180º and ∠A + ∠B = 180º
Now, ∠A + ∠D = 180º
⇒ ∠A + 115º = 180º [∵ ∠D = 115º (given)]
⇒ ∠A = 65º and ∠A + ∠B = 180º
⇒ 65º + ∠B = 180º ⇒ ∠B = 115º
Thus, ∠A = 65º and ∠B = 115º
Example 7: In figure, AB = AC, ∠EAD = ∠CAD and
CD || AB. Show that ABCD is a parallelogram.

Solution: In ∆ABC, AB = AC [Given]
⇒ ∠ABC = ∠ACB ….(1)
(Angles opposite the equal sides are equal)
∠EAD = ∠CAD[Given] ….(2)
Now, ∠EAC = ∠ABC + ∠ACB
[An exterior angle is equal to sum of two interior opposite angles of a triangles]
⇒ ∠EAD + ∠CAD = ∠ABC + ∠ACB
⇒ ∠CAD + ∠CAD = ∠ACB + ∠ACB
By (1) and (2)
⇒ 2∠CAD = 2∠ACB
⇒ ∠CAD = ∠ACB
⇒ BC | | AD
Also, CD | | AB [Given]
Thus, we have both pairs of opposite sides of quadrilateral ABCD parallel. Therefore, ABCD is a parallelogram.
Example 8: ABCD is a parallelogram and line segments AX,CY are angle bisector of ∠A and ∠C respectively then show AX || CY.

Solution: Since opposite angles are equal in a parallelogram. Therefore, in parallelogram ABCD, we have ∠A = ∠C
⇒ 1/2 ∠A = 1/2 ∠C
⇒ ∠1 = ∠2 ….(i)
[∵ AX and CY are bisectors of ∠A and ∠C respectively]
Now, AB || DC and the transversal CY intersects them.
∴ ∠2 = ∠3 …(ii)
[∵ Alternate interior angles are equal]
From (i) and (ii), we get
∠1 = ∠3
Thus, transversal AB intersects AX and YC at A and Y such that ∠1 = ∠3 i.e. corresponding angles are equal.
∴ AX || CY
Example 9: In the adjoining figure, a point O is taken inside an equilateral quad. ABCD such that OB = OD. Show that A, O and C are in the same straight line.

Solution: Given a quad. ABCD in which AB = BC
= CD = DA and O is a point within it such that OB = OD.
To prove ∠AOB + ∠COB = 180º
Proof In ∆OAB and OAD, we have
AB = AD (given)
OA = OA (common)
and OB = OD (given)
∴ ∆OAB ≅ ∆OAD
∴ ∠AOB = ∠AOD ….(i) (c.p.c.t.)
Similarly, ∆OBC ≅ ∆ODC
∴∠COB = ∠COD ….(ii)
Now, ∠AOB + ∠COB + ∠COD + ∠AOD
= 360º [∠ at a point]
⇒ 2(∠AOB + ∠COB) = 360º
⇒ ∠AOB + ∠COB = 180º
Example 10: In figure AN and CP are perpendiculars to the diagonal BD of a parallelogram ABCD. Prove that:
(i) ∆ADN ≅ ∆CBP (ii) AN = CP

Solution: Since ABCD is a parallelogram.
∴ AD || BC
Now, AD || BC and transversal BD intersects them at B and D.
∴ ∠1 = ∠2
[∵ Alternate interior angles are equal]
Now, in ∆s ADN and CBP, we have
∠1 = ∠2
∠AND = ∠CPD and, AD = BC
[∵ Opposite sides of a ||gm are equal]
So, by AAS criterion of congruence
∆ADN ≅ ∆CBP
AN = CP
[∵ Corresponding parts of congruent triangles are equal]
Example 11: In figure, ABCD is a trapezium such that AB || CD and AD = BC.

BE || AD and BE meets BC at E.
Show that (i) ABED is a parallelogram.
(ii) ∠A + ∠C = ∠B + ∠D = 180º.
Solution: Here, AB || CD (Given)
⇒ AB || DE ….(1)
Also, BE || AD (Given) ….(2)
From (1) and (2),
ABED is a parallelogram
⇒ AD = BE ….(3)
Also, AD = BC (Given) ….(4)
From (3) and (4),
BE = BC
⇒ ∠BEC = ∠BCE ….(5)
Also, ∠BAD = ∠BED
(opposite angles of parallelogram ABED)
i.e., ∠BED = ∠BAD ….(6)
Now, ∠BED + ∠BEC = 180º (Linear pair of angles)
⇒ ∠BAD + ∠BCE = 180º
By (5) and (6)
⇒ ∠A + ∠C = 180º
Similarly, ∠B + ∠D = 180º
Example 12: In figure ABCD is a parallelogram and ∠DAB = 60º. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD.

Solution: We have, ∠DAB = 60º
∠A + ∠B = 180º
∴ 60º + ∠B = 180º ⇒ ∠B = 120º
Now, AB || DC and transversal AP intersects them.
∴ ∠PAB = ∠APD
⇒ ∠APD = 30º [∵ ∠PAB = 30º]
Thus, in ∆APD, we have
∠PAD = ∠APD [Each equal to 30º]
⇒ AD = PD …. (i)
[∵ Angles opposite to equal sides are equal] Since BP is the bisector of ∠B. Therefore,
∠ABP = ∠PBC = 60º
Now, AB || DC and transversal BP intersects them.
∴ ∠CPB = ∠ABP
⇒ ∠CPB = 60º [∵ ∠ABP = 60º]
Thus, in ∆CBP, we have
∠CBP = ∠CPB [Each equal to 60º]
⇒ CP = BC
∵ [Sides opp, to equal angles are equal]
⇒ CP = AD …. (ii)
[∵ ABCD is a parallelogram ∴ AD = BC]
From (i) and (ii), we get
PD = CP
⇒ P is the mid point of CD.
Example 13: Prove that the line segments joining the mid-point of the sides of a quadrilateral forms a parallelogram.
Solution: Points E, F, G and H are the mid-points of the sides AB, BC, CD and DA respectively, of the quadrilateral ABCD. We have to prove that EFGH is a parallelogram.

Join the diagonal AC of the quadrilateral ABCD.
Now, in ∆ABC, we have E and F mid-points of the sides BA and BC.
⇒ EF || AC
and EF = 1/2 AC …. (1)
Similarly, from ∆ADC, we have
GH || AC
and GH = 1/2 AC ….(2)
Then from (1) and (2), we have
EF || GH
and EF = GH
This proves that EFGH is a parallelogram.
Example 14: In figure ABCD is a parallelogram and X, Y are the mid-points of sides AB and DC respectively. Show that AXCY is a parallelogram.
Solution: Since X and Y are the mid-points of AB and DC respectively. Therefore,
AX = 1/2 AB and CY = 1/2 DC … (i)
But, AB = DC [∵ ABCD is a parallelogram]

⇒ 1/2 AB = 1/2 DC
⇒ AX = CY …. (ii)
Also, AB || DC
⇒ AX || YC …. (iii)
Thus, in quadrilateral AXCY, we have
AX || YC and AX = YC
[From (ii) and (iii)]
Hence, quadrilateral AXCY is a parallelogram.
Example 15: Prove that the line segments joining the mid-points of the sides of a rectangle forms a rhombus.
Solution: P, Q, R and S are the mid-points of the sides AB, BC, CD and DA of the rectangle ABCD.


Example 16: In figure ABCD is a parallelogram and X and Y are points on the diagonal BD such that
DX = BY. Prove that
(i) AXCY is a parallelogram
(ii) AX = CY, AY = CX
(iii) ∆AYB ≅ ∆CXD
Solution: Given : ABCD is a parallelogram. X and Y are points on the diagonal BD such that
DX = BY
To Prove:
(i) AXCY is a parallelogram
(ii) AX = CY, AY = CX
(iii) ∆AYB ≅ ∆CXD
C Construction : join AC to meet BD at O.
Proof:
(i) We know that the diagonals of a parallelogram bisect each other. Therefore, AC and BD bisect each other at O.

∴ OB = OD
But, BY = DX
∴ OB – BY = OD – DX
⇒ OY = OX
Thus, in quadrilateral AXCY diagonals AC and XY are such that OX = OY and OA = OC i.e. the diagonals AC and XY bisect each other.
Hence, AXCY is a parallelogram.
(ii) Since AXCY is a parallelogram
∴ AX = CY and AY = CX
(iii) In triangles AYB and CXD, we have
AY = CX [From (ii)]
AB = CD
[∵ ABCD is a parallelogram]
BY = DX [Given]
So, by SSS-criterion of congruence, we have
∆AYB ≅ ∆CXD
Example 17: In fig. ABC is an isosceles triangle in which AB = AC. CP || AB and AP is the bisector
of exterior ∠CAD of ∆ABC. Prove that
∠PAC = ∠BCA and ABCP is a parallelogram.
Solution: Given : An isosceles ∆ABC having
AB = AC.AP is the bisector of ext ∠CAD and CP || AB.
To Prove: ∠PAC = ∠BCA and ABCP
Proof: In ∆ABC, we have
AB = AC [Given]
⇒ ∠1 = ∠2 …. (i)
∵ Angles opposite to equal sides in a ∆ are equal
Now, in ∆ ABC, we have
ext ∠CAD = ∠1 + ∠2

⇒ ext ∠CAD = 2∠2 [∵ ∠1 = ∠2 (from (i))]
⇒ 2∠3 = 2∠2
[∵ AP is the bisector of ext.∠CAD ∴∠CAD = 2∠3]
⇒ ∠3 = ∠2
Thus, AC intersects lines AP and BC at A and C respectively such that ∠3 = ∠2
i.e., alternate interior angles are equal.
Therefore, AP || BC.
But, CP || AB [Gvien]
Thus, ABCP is a quadrilateral such that
AP || BC and CP || AB.
Hence, ABCP is a parallelogram.
Example 18: In the given figure, ABCD is a square and ∠PQR = 90º. If PB = QC = DR, prove that

(i) QB = RC, (ii) PQ = QR, (iii) ∠QPR = 45º.
Solution: BC = DC, CQ = DR ⇒ BC – CQ = ∆CDR
⇒ QB = RC
From ∆CQR, ∠RQB = ∠QCR + ∠QRC
⇒ ∠RQP + ∠PQB = 90º + ∠QRC
⇒ 90º + ∠PQB = 90º + ∠QRC
Now, ∆RCQ ≅ ∆QBP and therefore,
QR = PQ
PQ = QR ⇒ ∠QPR = ∠PRQ
Bur, ∠QPR + ∠PRQ = 90º.
So, ∠QPR = 45º
Example 19: Prove that in a parallelogram
(i) opposite sides are equal
(ii) opposite angles are equal
(iii) each diagonal bisects the parallelogram
Solution: Given: A ||gm ABCD in which AB || DC and AD || BC.
To prove: (i) AB = CD and BC = AD;
(ii) ∠B = ∠D and ∠A = ∠C,
(iii) ∆ABC = ∆CDA and ∆ABD = ∆CDB
Construction join A and C.
In ∆ABC and CDA, we have,

∠1 = ∠2
[Alt. int. ∠, as AB || DC and CA cuts them]
∠3 = ∠4
[Alt. int. ∠, as BC || AD and CA cuts them]
AC = CA (common)
∴ ∆ABC ≅ ∆CDA [AAS-criterial]
(i) ∆ABC ≅ ∆CDA (proved)
∴ AB = CD and BC = AD (c.p.c.t.)
(ii) ∆ABC ≅ ∆CDA (proved)
∴ ∠B = ∠D (c.p.c.t.)
Also, ∠1 = ∠2 and ∠3 = ∠4
∠1 + ∠4 = ∠2 + ∠3 ⇒ ∠A = ∠C
Hence, ∠B = ∠D and ∠A = ∠C
(iii) Since ∆ABC ≅ ∆CDA and congruent triangles are equal in area,
So we have ∆ABC = ∆CDA
Similarly, ∆ABD = ∆CDB
Example 20: If the diagonals of a parallelogram are perpendicular to each other, prove that it is a rhombus.
Solution: Since the diagonals of a ||gm bisect each other,

we have, OA = OC and OB = OD.
Now, in ∆AOD and COD, we have
OA = OC, ∠AOD = ∠COD =90°
and OD is common
∴ ∆AOD ≅ ∆COD
∴ AD = CD (c.p.c.t.)
Now, AB = CD and AD = BC
(opp. sides of a ||gm)
and AD = CD (proved)
∴ AB = CD = AD = BC
Hence, ABCD is a rhombus.
Example 21: PQRS is a square. Determine ∠SRP.
Solution: PQRS is a square.
∴ PS = SR and ∠PSR = 90°
Now, in ∆ PSR, we have
PS = SR

⇒ ∠1 = ∠2
∵ Angles opposite to equal sides in a ∆ are equal
But, ∠1 + ∠2 + ∠PSR = 180º
∴ 2∠1 + 90° = 180º [∵ ∠PSR = 90°]
⇒ 2∠1 = 90°
⇒ ∠1 = 45°
Example 22: In the adjoining figure, ABCD is a rhombus. If ∠A = 70º, find ∠CDB
Sol.

We have ∠C = ∠A = 70º
(opposite ∠ of a ||gm)
Let ∠CDB = xº
In ∆CDB, we have
CD = CB ⇒∠CBD = ∠CDB = xº
∴ ∠CDB + ∠CBD + ∠DCB = 180º
(angles of a triangle)
⇒ xº + xº + 70º = 180º
⇒ 2x = 110, i.e., x = 55
Hence, ∠CDB = 55º
Example 23: ABCD is a rhombus with ∠ABC = 56°. Determine ∠ACD.
Solution: ABCD is a parallelogram

⇒ ∠ABC = ∠ADC
⇒ ∠ADC = 56° [∵ ∠ABC = 56° (Given)]
⇒ ∠ODC = 28° [∵ ∠ODC = 1/2 ∠ADC]
Now, ∆OCD we have,
∠OCD + ∠ODC + ∠COD = 180°
⇒ ∠ODC + 28° + 90° = 180°
⇒ ∠OCD = 62° ⇒∠ACD = 62°.
Example 24: Prove that the line segment joining the
mid-points of the diagonals of a trapezium is parallel to each of the parallel sides and is equal to half the difference of these sides.
Solution: Given: A trapezium ABCD in which
AB || DC and P and Q are the mid-points of its diagonals AC and BD respectively.

To Prove: (i) PQ || AB or DC
(ii) PQ = 1/2 (AB – DC)
Construction: Join DP and produce DP to meet AB in R.
Proof: Since AB || DC and transversal AC cuts them at A and C respectively.
∠1 = ∠2 …. (i)
[∴ Alternate angles are equal]
Now, in ∆s APR and DPC, we have
∠1 = ∠2 [From (i)]
AP = CP [∵ P is the mid-point of AC]
and, ∠3 = ∠4 [Vertically opposite angles]
So, by ASA criterion of congruence
∆APR ≅ ∆DPC
⇒ AR = DC and PR = DP ….(ii)
[∵ Corresponding parts of congruent triangles are equal]
In ∆DRB, P and Q are the mid-points of sides DR and DB respectively.
∴ PQ || RB
⇒ PQ || AB [∵ RB is a part of AB]
⇒ PQ || AB and DC [∵ AB || DC (Given)]
This proves (i).
Again, P and Q are the mid-points of sides DR and DB respectively in ∆DRB.
∴ PQ = 1/2 RB ⇒ PQ = 1/2 (AB – AR)
⇒ PQ = 1/2 (AB – DC) [From (ii), AR = DC]
This proves (ii).
Example 25: In the adjoining figure, ABCD is parallelogram and X, Y are the points on diagonal BD such that DX = BY. Prove that CXAY is a parallelogram.

Solution: Join AC, meeting BD at O.
Since the diagonals of a parallelogram bisect each other, we have OA = OC and OD = OB.
Now, OD = OB and DX = BY
⇒ OD – DX = OB – BY ⇒ OX = OY
Now, OA = OC and OX = OY
∴ CXAY is a quadrilateral whose diagonals bisect each other.
∴ CXAY is a ||gm
Example 26: Prove that the four triangles formed by joining in pairs, the mid-points of three sides of a triangle, are concurrent to each other.
Solution: Given: A triangle ABC and D,E,F are the mid-points of sides BC, CA and AB respectively.
To Prove:
∆ AFE ≅ ∆FBD ≅ ∆EDC ≅ ∆DEF.
Proof: Since the segment joining the mid-points of the sides of a triangle is half of the third side. Therefore,

DE = 1/2 ⇒ DE = AF = BF …. (i)
EF = 1/2 ⇒ EF = BD = CD …. (ii)
DF = 1/2 ⇒ DF = AE = EC ….(iii)
Now, in ∆s DEF and AFE, we have
DE = AF [From (i)]
DF = AE [From (ii)]
and, EF = FE [Common]
So, by SSS criterion of congruence,
∆ DEF ≅ ∆AFE
Similarly, ∆DEF ≅ ∆FBD and ≅ DEF ≅ ∆EDC
Hence, ∆ AFE ≅ ∆FBD ≅ ∆EDC ≅ ∆DEF.
Example 27: In fig, AD is the median and DE || AB. Prove that BE is the median.
Solution: In order to prove that BE is the median, it is sufficient to show that E is the mid-point of AC.
Now, AD is the median in ∆ABC
⇒ D is the mid-point of BC.

Since DE is a line drawn through the mid-point of side BC of ∆ABC and is parallel to AB (given). Therefore, E is the mid-point of AC. Hence, BE is the median of ∆ABC.
Example 28: Let ABC be an isosceles triangle with AB = AC and let D,E,F be the mid-points of BC, CA and AB respectively. Show that
AD ⊥ FE and AD is bisected by FE.
Solution: Given: An isosceles triangle ABC with D, E and F as the mid-points of sides BC, CA and AB respectively such that AB = AC. AD intersects FE at O.
To Prove: AD ⊥ FE and AD is bisected by FE.
Constructon: Join DE and DF.
Proof: Since the segment joining the mid-points of two sides of a triangle is parallel to third side and is half of it. Therefore,
DE || AB and DE = 1/2 AB
Also, DF || AC and DF = 1/2 AC

But, 1/2 AB = 1/2 AC [Given]
⇒ AB = AC
⇒ DE = DF …. (i)
Now, DE = 1/2 AB ⇒ DE = AF …. (ii)
and, DF = 1/2 AC ⇒ DF = AE …(iii)
From (i), (ii) and (iii) we have
DE = AE = AF = DF
⇒ DEAF is a rhombus.
⇒ Diagonals AD and FE bisect each other at right angle.
AD ⊥ FE and AD is bisected by FE.
Example 29: ABCD is a parallelogram. P is a point on AD such that AP = 1/3 AD and Q is a point on BC such that CQ = 1/3 BP. Prove that AQCP is a parallelogram.

Solution: ABCD is a parallelogram.
⇒ AD = BC and AD || BC
⇒ 1/3 AD = 1/3 BC and AD || BC
⇒ AP = CQ and AP || CQ
Thus, APCQ is a quadrilateral such that one pair of opposite side AP and CQ are parallel and equal.
Hence, APCQ is a parallelogram.
Example 30: In fig. D,E and F are, respectively the mid- points of sides BC, CA and AB of an equilateral triangle ABC. Prove that DEF is also an equilateral triangle.
Solution: Since the segment joining the mid-points of two sides of a triangle is half of the third side. Therefore, D and E are mid-points of BC and AC respectively.


Example 31: P,Q and R are, respectively, the mid-points of sides BC, CA and AB of a triangle ABC. PR and BQ meet at X. CR and PQ meet at Y. Prove that XY = 1/4 BC
Solution: Given: A ∆ABC with P,Q and R as the mid-points of BC, CA and AB respectively. PR and BQ meet at X and CR and PQ meet at Y.
Construction: Join “X and Y.

Proof: Since the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it. Therefore, Q and R are mid-points of AC and AB respectively.

Similarly, Y is the mid-point of PQ.
Now, consider ∆PQR. XY is the line segment joining the mid-points of sides PR and PQ.
∴ XY = 1/2 RQ …. (i)
But RQ = 1/2 BC [From (i)]
Hence, XY = 1/4 BC
Example 32: Show that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
Solution: Given: A square ABCD in which P, Q, R, S are the mid-points of sides AB, BC, CD, DA respectively. PQ, QR, RS and SP are joined.
To Prove: PQRS is a square.
Construction: Join AC and BD.

Proof : In ∆ABC, P and Q are the mid-points of sides AB and BC respectively.
∴ PQ || AC and PQ = 1/2 AC …. (i)
In ∆ADC, R and S are the mid-points of CD and AD respectively.
∴ RS || AC and RS = 1/2 AC ….(ii)
From (i) and (ii), we have
PQ || RS and PQ = RS ….(iii)
Thus, in quadrilateral PQRS one pair of opposite sides are equal and parallel.
Hence, PQRS is a parallelogram.
Now, in ∆s PBQ and RCQ, we have
PB = RC

Now, PQ || AC [From (i)]
⇒ PM || NO ….(vi)
Since P and S are the mid-points of AB and AD respectively.
PS || BD
⇒ PM || MO ….(vii)
Thus, in quadrilateral PMON, we have
PM || NO [From (vi)]
PN || MO [From (vii)]
So, PMON is a parallelogram.
⇒ ∠MPN = ∠MON
⇒ ∠MPN = ∠BOA [∵ ∠MON = ∠BOA]
⇒ ∠MPN = 90°
⇒ ∠QPS = 90°
Thus, PQRS is a quadrilateral such that
PQ = QR = RS = SP and ∠QPS = 90°.
Hence, PQRS is a square.
Example 33: ∆ABC is a triangle right angled at B ; and P is the mid-point of AC. Prove that PB = PA = 1/2 AC.
Solution: Given : ∆ABC right angled at B, P is the mid-point of AC.
To Prove: PB = PA = 1/2 AC.
Construction: Through P draw PQ || BC meeting AB at Q.

Proof: Since PQ || BC. Therefore,
∠AQP = ∠ABC [Corresponding angles]
⇒ ∠AQP = 90° [∵ ∠ABC = 90°]
But, ∠AQP + ∠BQP = 180°
[∵ ∠AQP & ∠BQP are angles of a linear pair]
∴ 90° + ∠BQP = 180°
⇒ ∠BQP = 90°
Thus, ∠AQP = ∠BQP = 90°
Now, in ∆ABC, P is the mid-point of AC and
PQ || BC. Therefore, Q is the mid-point of AB i.e, AQ = BQ.
Consider now ∆s APQ and BPQ.
we have, AQ = BC [Proved above]
∠AQP = ∠BQP [From (i)]
and, PQ = PQ
So, by SAS cirterion of congruence
∆APQ ≅ ∠BPQ
⇒ PA = PB
Also,
PS = 1/2 AC, since P is the mid-point of AC
Hence, PA = PB = 1/2 AC.
Example 34: Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
Solution: Given: A rectangle ABCD in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined.
To Prove: PQRS is rhombus.
Construction: Join AC.
Proof: In ∆ABC, P and Q are the mid-points of sides AB and BC respectively.
∴ PQ || AC and PQ = AC …. (i)
In ∆ ADC, R and S are the mid-points of CD and AD respectively.

∴ SR || AC and SR = 1/2 AC …. (ii)
From (i) and (ii), we get
PQ || SR and PQ = SR ….(iii)
⇒ PQRS is a parallelogram.
Now, ABCD is a rectangle.
⇒ AD = BC ⇒ 1/2 AD = 1/2 BC
⇒ AS = BQ ….(iv)
In ∆s APS and BPQ , we have
AP = BP [∴P is the mid-point of AB]
∠PAS = ∠PBQ [Each equal to 90°]
and, AS = BQ [From (iv)]
So, by SAS criterion of congruence
∆APS ≅ ∆BPQ
PS = PQ ….(v)
[∵ Corresponding parts of congruent triangles are equal]
From (iii) and (v), we obtain that PQRS is a parallelogram such that PS = PQ i.e., two adjacent sides are equal.
Hence, PQRS is a rhombus.