Solving Linear Inequalities
Solving linear inequalities is the same as solving linear equations with one very important exception…
When you multiply or divide an inequality by a negative value, it changes the direction of the inequality.
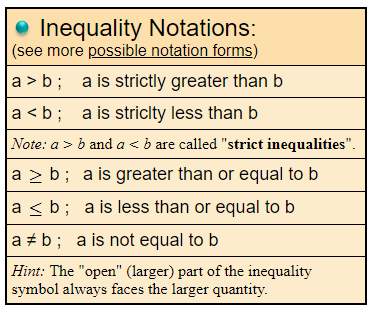
Basic Properties of Inequalities: (properties apply to symbols >, <, ≥, ≤)

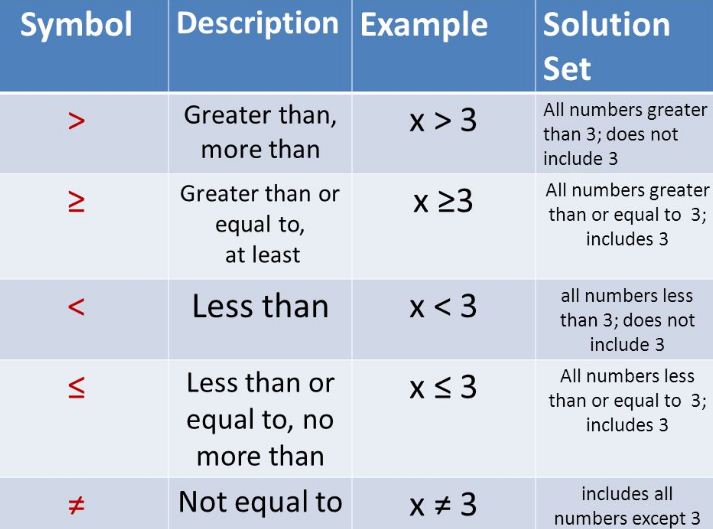
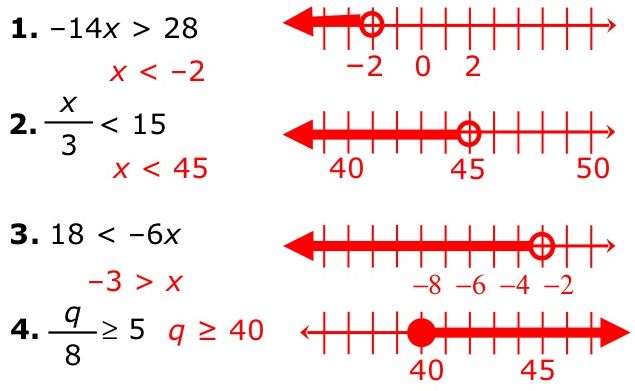
Inequalities with one variable:
Example 1: Solve and graph the solution set of: 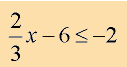
Proceed as you would when solving a linear equation:
Add 6 to both sides.
Multiply both sides by \(\frac { 3 }{ 2 } \).
Note: The direction of the inequality stays the same since we did NOT multiply by a negative value.
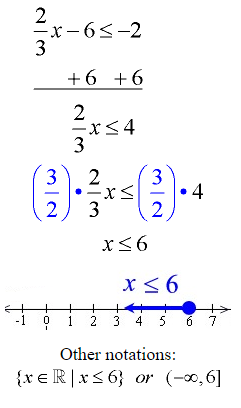
Graph using a closed circle for 6 (since x can equal 6) and an arrow to the left (since our symbol is less than or equal to).
Example 2: Solve and graph the solution set of: 5(x – 3) > 10
Distribute (remove the parentheses).
Add 15 to both sides.
Divide both sides by 5.
Note: The direction of the inequality stays the same since we did NOT multiply by a negative value.
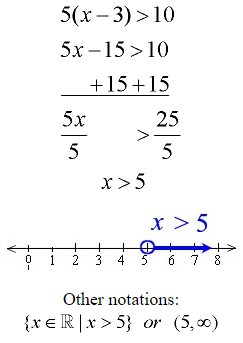
Graph using a open circle for 5 (since x can NOT equal 5) and an arrow to the right (since our symbol is greater than).
Example 3: Solve and graph the solution set of: 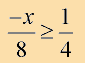
Multiply both sides by the least common denominator, which is 8.
Divide both sides by -1, and flip the direction of the inequality.
Note: The direction of the inequality was reversed since we divided by a negative value (-1).
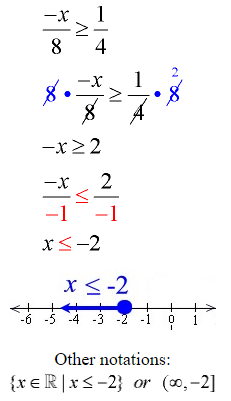
Graph using a closed circle for -2 (since x can equal -2) and an arrow to the left (since our symbol is less than or equal to).
Example 4: Solve and graph the solution set of: 4(x – 1) > 3(x – 2)
Distribute across both sets of parentheses.
Subtract 3x from both sides.
The solution is easier if you move the smaller x value.
Add 4 to both sides.
Note: The direction of the inequality stays the same since we did NOT multiply or divide by a negative value.
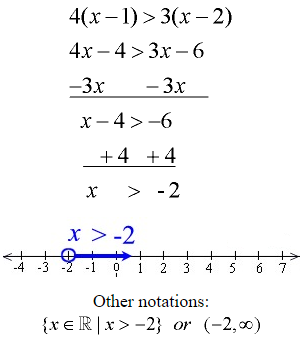
Graph using an open circle for -2 (since x can not equal -2) and an arrow to the right (since our symbol is greater than).
Example 5: Solve and graph the solution set of: 4(2x + 1) < 8x + 4
Distribute across the parentheses.
Subtract 8x from both sides.
Notice the FALSE result.
The solution to this inequality is the “empty set” (∅). There are no x-values which will make this inequality true.
There is nothing to be graphed.
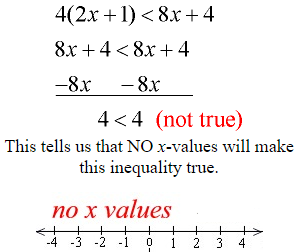
In this problem, the left side of the inequality is simply another way of writing the right side of the inequality. The two sides are EQUAL to one another. Since a quantity can never be less than itself, this inequality is never true.
Example 6: Solve and graph the solution set of: 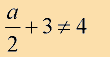
Proceed as you would when solving a linear equation:
Subtract 3 from both sides.
Multiply both sides by 2.
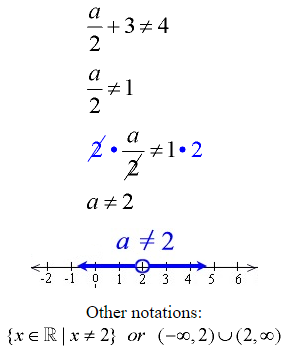
The solution to this inequality is all real numbers except 2. The number 2 is the only value which makes this inequality false, since:
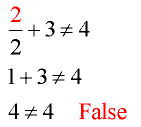
Example 7: Solve and graph the solution set of: 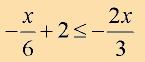
Hint: In this problem, the negative signs appear in front of the two fractional terms. You can place the negative sign in the numerator, or the denomoniator, since
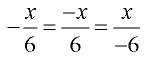
This example places the negative sign in the numerators.
Multiply all terms by the least common denominator (which is 6).
Add 4x to both sides.
The solution is easier if you move the smaller x value.
Be sure to write the 0 on the right side.
Subtract 12 from both sides.
Divide both sides by 3.
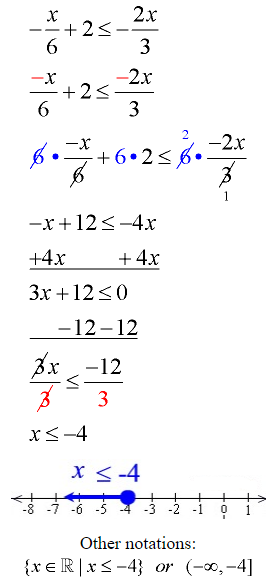
Example 8: Solve for x: ax > 6a
At first glance, it seems that dividing both sides by a will solve the problem.
But We just don’t know if a is a positive value or a negative value. If a is positive, our solution of x > 6 will be true.
But if a is negative, we need to reverse the direction of the inequality, and the solution is x < 6.
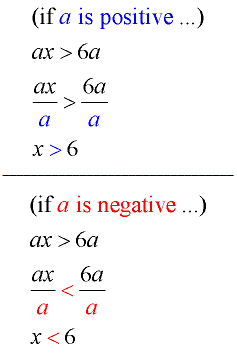
Since we do not know the value of a, we cannot state a solution to this problem.
Therefore, there is No Solution!