Review of Exponents

Review of Exponents

1. Exponents are the mathematician’s shorthand.
2. In general, the format for using exponents is:
   (base)^exponent
   where the exponent tells you how many of the base are being multiplied together.
3. Consider: 2 • 2 • 2 is the same as 2³, since there are three 2’s being multiplied together.
   Likewise, 5 • 5 • 5 • 5 = 54, because there are four 5’s being multiplied together.
4. Exponents are also referred to as “powers”.
   For example, 2³ can be read as “two cubed” or as “two raised to the third power”.

Read More:

• What is an Exponent?
• What are Laws of Exponents?
• Surds

Exponents of Negative Values

When we multiply negative numbers together, we must utilize parentheses to switch to exponent notation.
(-4)(-4)(-4)(-4)(-4)(-4) = (-4)⁶

The examples below show that (-4)⁶ and -4⁶ are not the same.

The missing parentheses mean that -4⁶ will multiply six 4’s together first (by order of operations), and then take the negative of that answer.

Example:
(-3)² = (-3) × (-3) = +9
The 2 is “attached” to the parentheses, so everything inside the parentheses is squared.

-3² is not the same as (-3)²
-3² = -(3²) 
The 2 is “attached” to the 3, but not to the negative sign.
 -3² = -(3²) = -(3 × 3) = -(9) = -9
The expression -3² (with missing parentheses) means to multiply two 3’s together first (by order of operations), and then take the negative of that answer.

Even powers of negative numbers allow for the negative values to be arranged in pairs. This pairing guarantees that the answer will always be positive.

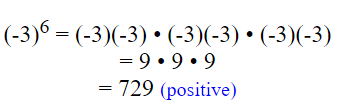
Odd powers of negative numbers, however, always leave one factor of the negative number not paired. This one lone negative term guarantees that the answer will always be negative.

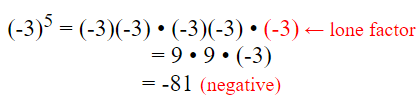
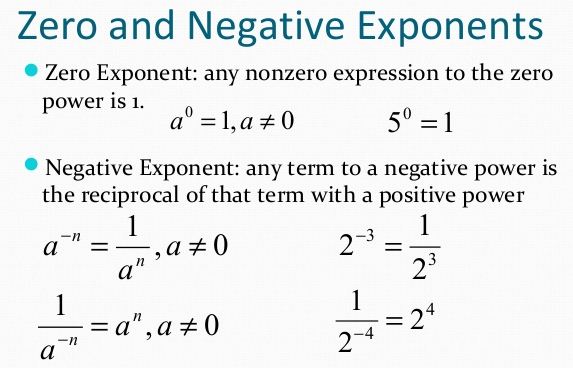
Zero Exponents

The number zero may be used as an exponent.
The value of any expression raised to the zero power is 1.
(Except zero raised to the zero power is undefined.)

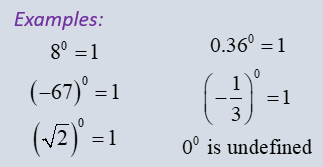
Negative Exponents

Negative numbers as exponents have a special meaning.

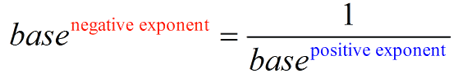
The rule is as follows:

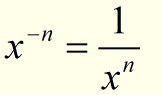
For example:

Exponents and Units

When working with units and exponents (or powers), remember to adjust the units appropriately.
(36 ft)³ = (36 ft) • (36 ft) • (36 ft)
= (36 • 36 • 36) (ft • ft • ft)
= 46656 ft³

Exponents can be very useful for evaluating expressions. It is also useful to learn how to use your calculator when working with exponents

Maths