What are Laws of Exponents?

Laws of Exponents

Law-1:
If a is any non-zero integer and m and n are whole numbers, then

a^m × aⁿ = a^{m + n}

Eg :

Therefore, in general, we write,

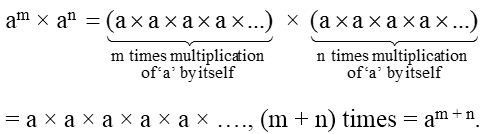
Read More:

Law-2:
If a and b are non-zero integers and m is a positive integer, then

a^m × b^m = (a × b)^m

Eg :
5³ × 3³ = (5 × 5 × 5) × (3 × 3 × 3)
= (5 × 3) × (5 × 3) × (5 × 3)
= 15 × 15 × 15 = (15)³
So, 5³ × 3³ = (5 × 3)³ = (15)³
Here, we find that 15 is the product of bases 5 and 3.
Also, if a and b are non-zero integers, then
a⁵ × b⁵ = (a × a × a × a × a) × (b × b × b × b × b)
= (a × b) (a × b) (a × b) (a × b) (a × b) = (ab)⁵

Law-3:
If a is a non-zero integer and m and n are two whole numbers such that m > n, then

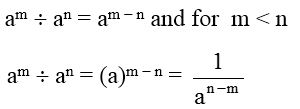
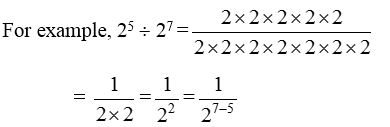When an exponential form is divided by another exponential form whose bases are same, then the resultant is an exponential form with same base but the exponent is the difference of the exponent of the divisor from the exponent of the dividend.

Law-4:
Division of exponential forms with the same exponents and different base:
If a and b are any two non-zero integers, have same exponent m then for a^m ÷ b^m, we write

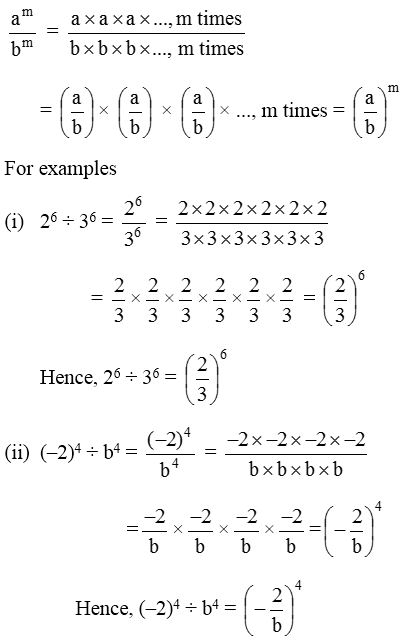
Law-5:
If ‘a’ be any non-zero integer and m and n any two positive integers then

[(a)^m]ⁿ = a^mn

Eg :
(2²)³ = 2² × 2² × 2² = 2^{2 + 2 +2} = 2⁶ = 2^{2 × 3}
(2⁷)² = 2⁷ × 2⁷ = 2^{7 +7} = 2¹⁴ = 2^{7 × 2}

Law-6:
Law of zero Exponent:
We know that

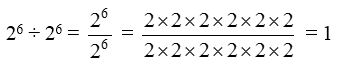
By using Law-3 of exponents, we have
2⁶ ÷ 2⁶ = 2^6–6 = 2⁰
Thus, 2⁰ = 1
In general a^m ÷ a^m = a^{m – m} = a⁰and also

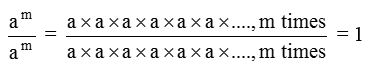
Hence, a⁰= 1
Any non-zero integer raised to the power 0 always results into 1.

Use Of Exponents In Expressing Large Numbers

We know that
100 = 10 × 10 = 10²,
1000 = 10 × 10 × 10 = 10³,
10000 = 10 × 10 × 10 × 10 = 10⁴
We can write a number followed by large number of zeroes in powers of 10.
For example, we can write the speed of light in vacuum = 300,000,000 m/s
= 3 × 1,00,000,000 m/s = 3 × 10⁸ m/s
= 30 × 10⁷ m/s = 300 × 10⁶ m/s
Similarly,
the age of universe = 8,000,000,000 years (app.)
= 8 × 10⁹ years (app.)
We can also express the age of universe as
80 × 10⁸ years or 800 × 10⁷ years, etc.
But generally the number which preceded the power of 10 should be less than 10. Such a notation is called standard or scientific notation.
So 8 × 10⁹ years is the standard form of the age of the universe.
Similarly, the standard form of the speed of light is 3 × 10⁸ m/s.

Eg: Write the following numbers in standard form :
(i) 4340000
(ii) 173000
(iii) 140000
Solution:
(i) It is clear that 4340000 = 434 × 10000
Also, 4340000 = 4.34 × 10⁶
∵ 434 = 4.34 × 100 = 4.34 × 10²
(ii) Also, 173000 = 1.73 × 10⁵
(iii) Also, 140000 = 1.4 × 10⁵

Laws of Exponents Problems with Solutions

1. Write in exponential form :
(i) (5 × 7)⁶ (ii) (–7n)⁵
Solution:
(i) (5 × 7)⁶
= (5 × 7) (5 × 7) (5 × 7) (5 × 7) (5 × 7) (5 × 7)
= (5 × 5 × 5 × 5 × 5 × 5) ( 7 × 7 × 7 × 7 × 7 × 7) = 5⁶ × 7⁶
Hence, (5 × 7)⁶ = 5⁶ × 7⁶
(ii) (–7n)⁵ = (–7n) (–7n) (–7n) (–7n) (–7n)
= (–7 × – 7 × – 7 × – 7 × –7) (n × n × n × n × n)
= (–7)⁵ × (n)⁵

2. Write the following in expanded form :

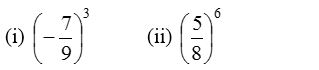
Solution:

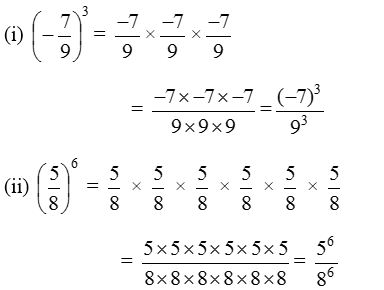
3. Find the value of :
(i) (3⁰ – 2⁰) × 5⁰
(ii) 2⁰ × 3⁰ × 4⁰
(iii) (6⁰ – 2⁰) × (6⁰ + 2⁰)
Solution:
(i) We have, (3⁰ – 2⁰) × 5⁰
Therefore, (1 – 1) × 1 = 0 × 1 = 0
[Since 3⁰ =1 , 2⁰ = 1]
(ii) We have, 2⁰ × 3⁰ × 4⁰ = (1 × 1 × 1) = 1
(iii) We have, (6⁰ – 2⁰) × (6⁰ + 2⁰)
= (1 – 1) × (1 + 1)
= 0 × 2 = 0.