Surds

Surds

Definition of surd

Any root of a number which can not be exactly found is called a surd.

Let a be a rational number and n is a positive integer. If the n^th root of x i.e., x^1/n is irrational, then it is called surd of order n.

Order of a surd is indicated by the number denoting the root.

For example, \(\sqrt { 7 } ,\sqrt [ 3 ]{ 9 } ,{ 11 }^{ 3/5 },\sqrt [ n ]{ 3 } \) are surds of second, third, fifth and n^th order respectively.

A second order surd is often called a quadratic surd, a surd of third order is called a cubic surd.

Read More:

• What is an Exponent?
• What are Laws of Exponents?
• Review of Exponents

Types of surds

1. Simple surds: A surd consisting of a single term. For example 2√3, 6√5, √5 etc.
2. Pure and mixed surds: A surd consisting of wholly of an irrational number is called pure surd.
   A surd consisting of the product of a rational number and an irrational number is called a mixed surd.
3. Compound surds: An expression consisting of the sum or difference of two or more surds.
4. Similar surds: If the surds are different multiples of the same surd, they are called similar surds.
5. Binomial surds: A compound surd consisting of two surds is called a binomial surd.
6. Binomial quadratic surds: Binomial surds consisting of pure (or simple) surds of order two i.e., the surds of the form a√b ± c√d or a ± b√c are called binomial quadratic surds.
   Two binomial quadratic surds which differ only in the sign which connects their terms are said to be conjugate or complementary to each other. The product of a binomial quadratic surd and its conjugate is always rational.
   For example: The conjugate of the surd 2√7 + 5√3 is the surd 2√7 – 5√3.

Properties of quadratic surds

1. The square root of a rational number cannot be expressed as the sum or difference of a rational number and a quadratic surd.
2. If two quadratic surds cannot be reduced to others, which have not the same irrational part, their product is irrational.
3. One quadratic surd cannot be equal to the sum or difference of two others, not having the same irrational part.
4. If a + √b = c + √d where a and c are rational, and √b, √d  are irrational, then a = c and b = d.

Rationalisation factors

If two surds be such that their product is rational, then each one of them is called rationalising factor of the other.
Thus each of 2√3 and √3 is a rationalising factor of each other. Similarly √3 + √2 and √3 – √2 are rationalising factors of each other, as (√3 + √2)(√3 – √2) = 1, which is rational.
To find the factor which will rationalize any given binomial surd:
Case I: Suppose the given surd is \(\sqrt [ p ]{ a } -\sqrt [ q ]{ b } \)
Let a^1/p = x, b^1/q = y  and let n be the L.C.M. of p and q. Then xⁿ and yⁿ are both rational.
Now xⁿ – yⁿ is divisible by x – y for all values of n, and xⁿ – yⁿ = (x – y)(x^n-1 + x^n-2y + x^n-3y² + ….. + y^n-1).
Thus the rationalizing factor is x^n-1 + x^n-2y + x^n-3y² + ….. + y^n-1 and the rational product is xⁿ – yⁿ.
Case II: Let the given surd be \(\sqrt [ p ]{ a } +\sqrt [ q ]{ b } \)
Let have the same meaning as in Case I.
(1) If n is even, then xⁿ – yⁿ is divisible by x + y and xⁿ – yⁿ = (x + y)(x^n-1 – x^n-2y + x^n-3y² – ….. – y^n-1).
Thus the rationalizing factor is x^n-1 – x^n-2y + x^n-3y² – ….. – y^n-1 and the rational product is xⁿ – yⁿ.
(2) If n is odd, xⁿ + yⁿ is divisible by x + y and xⁿ + yⁿ = (x + y)(x^n-1 – x^n-2y + x^n-3y² – ….. + y^n-1)
Thus the rationalizing factor is and the rational product is xⁿ + yⁿ.

Square roots of a +√b and a + √b + √c + √d where √b , √c , √d are Surds

Let  √(√a + √b) = √x + √y where x, y > 0 are rational numbers.

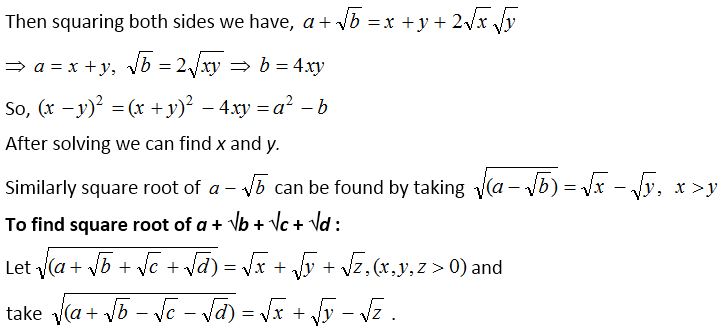
Then by squaring and equating, we get equations in x, y, z. On solving these equations, we can find the required square roots.

Cube root of a binomial quadratic surd

Equations involving surds

While solving equations involving surds, usually we have to square, on squaring the domain of the equation extends and we may get some extraneous solutions, and so we must verify the solutions and neglect those which do not satisfy the equation.
Note that from ax = bx, to conclude a = b is not correct. The correct procedure is x(a – b)=0 i.e. x = 0 or a = b. Here, necessity of verification is required.