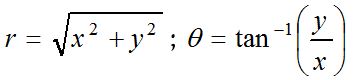Polar and Cartesian Coordinates
Cartesian co-ordinates of a point
This is the most popular co-ordinate system.
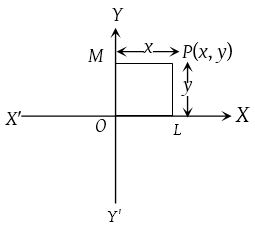Axis of x: The line XOX’ is called axis of x.
Axis of y: The line YOY’ is called axis of y.
Co-ordinate axes: x axis and y axis together are called axis of co-ordinates or axes of reference.
Origin: The point ‘O’ is called the origin of co-ordinates or the origin.
Let OL = x and OM = y which are respectively called the abscissa (or x-coordinate) and the ordinate (or y-coordinate). The co-ordinate of P are (x, y).
Here, co-ordinates of the origin is (0, 0). The y co-ordinates of every point on x-axis is zero.
The x co-ordinates of every point on y-axis is zero.
Oblique axes: If both the axes are not perpendicular then they are called as oblique axes.
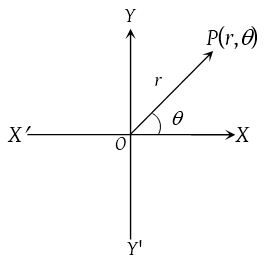
Polar co-ordinates
Let OX be any fixed line which is usually called the initial line and O be a fixed point on it. If distance of any point P from the O is ‘r’ and ∠XOP = θ, then (r, θ ) are called the polar co-ordinates of a point P.
To convert from Polar Coordinates (r,θ) to Cartesian Coordinates (x,y):
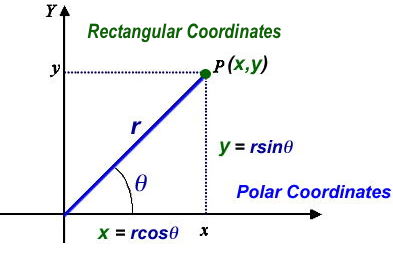If (x, y) are the cartesian co-ordinates of a point P, then x = r cos θ; y = r sin θ; and
