A Plus Topper

Improve your Grades

Math Labs with Activity - Pythagoras' theorem (Method 6)

by

Math Labs with Activity – Pythagoras theorem (Method 6)

OBJECTIVE

To verify Pythagoras’ theorem (Method 6)

Materials Required

  1. A piece of cardboard
  2. Two sheets of white paper
  3. A drawing sheet
  4. A pair of scissors
  5. A geometry box
  6. A tube of glue

Theory
Pythagoras’ theorem: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Procedure
Step 1: Paste a sheet of white paper on the cardboard.
On this paper, draw a right-angled triangle ABC, right angled at C. Let the lengths of the sides AB, BC and CA.be c, a and b units respectively.
Step 2: Construct the following three squares:

  1. square DEBA on the side AB with each side measuring c units
  2. square BFGC on the side BC with each side measuring a units
  3. square ACHI on the side AC with each side measuring b units

The diagram will appear as shown in Figure 14.1.
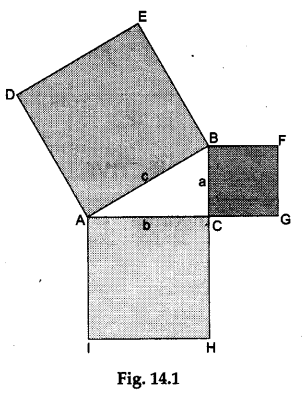
Math Labs with Activity - Pythagoras' theorem (Method 6) 1
Step 3: On the other sheet of paper, make exact copies of each one of the three squares. Also, make eight exact copies of the ΔABC. Shade the squares BFGC and ACHI differently.
Step 4: Cut all the three squares and the eight triangles.
Step 5: Arrange the square DEBA and the four triangles as shown in Figure 14.2, and paste this arrangement – on the upper half of a drawing sheet.
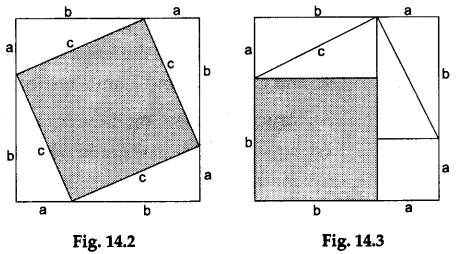
Math Labs with Activity - Pythagoras' theorem (Method 6) 2
Step 6: Arrange the remaining two squares (i.e., BFGC and ACHI) and the four triangles as shown in Figure 14.3. Paste this arrangement on the lower half of the drawing sheet.

Observations and Calculations
We observe that each of the two arrangements (shown in Figures 14.2 and 14.3) forms a square of side (a+b) units. Therefore, both the squares have the equal area.
Now, if we remove the four triangles from each one of the two figures, the areas of the remaining figures must still be the same.
So, area of the square in Figure 14.2 = sum of the areas of the squares in Figure 14.3,
i.e., c² = a² + b².
Applying this result on the right-angled ΔABC we conclude that the square of the hypotenuse of the right-angled ΔABC is equal to the sum of the squares of the other two sides.

Result
Pythagoras’ theorem is verified.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs