Pythagoras Theorem

Pythagoras Theorem

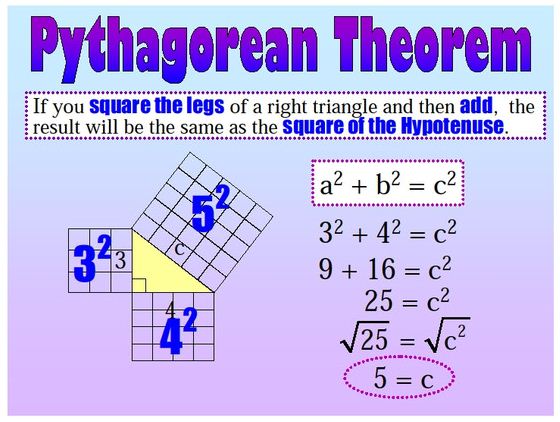
Theorem 1: In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Given: A right-angled triangle ABC in which B = ∠90º.
To Prove: (Hypotenuse)² = (Base)² + (Perpendicular)².
i.e., AC² = AB² + BC²
Construction: From B draw BD ⊥ AC.

Proof: In triangle ADB and ABC, we have
∠ADB = ∠ABC         [Each equal to 90º]
and, ∠A = ∠A           [Common]
So, by AA-similarity criterion, we have
∆ADB ~ ∆ABC
\(\Rightarrow \frac{AD}{AB}=\frac{AB}{AC}\)   [∵ In similar triangles corresponding sides are proportional]
⇒ AB² = AD × AC                                ….(i)
In triangles BDC and ABC, we have
∠CDB = ∠ABC             [Each equal to 90º]
and, ∠C = ∠C                 [Common]
So, by AA-similarity criterion, we have
∆BDC ~ ∆ABC
\(\Rightarrow \frac{DC}{BC}=\frac{BC}{AC}\)         [∵ In similar triangles corresponding sides are proportional]
⇒ BC² = AC × DC                              ….(ii)
Adding equation (i) and (ii), we get
AB² + BC² = AD × AC + AC × DC
⇒ AB² + BC² = AC (AD + DC)
⇒ AB² + BC² = AC × AC
⇒ AC² = AB² + BC²
Hence, AC² = AB² + BC²
The converse of the above theorem is also true as proved below.

Read also:

• Pythagorean Theorem in Algebra
• Pythagorean Theorem

Theorem 2: (Converse of Pythagoras Theorem).
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the side is a right angle.
Given: A triangle ABC such that AC² = AB² + BC²

Construction: Construct a triangle DEF such that DE = AB, EF = BC and ∠E = 90º,
Proof: In order to prove that B = ∠90º, it is sufficient to show that ∆ABC ~ ∆DEF.
For this we proceed as follows :
Since  ∆DEF is a right angled triangle with right angle at E. Therefore, by Pythagoras theorem, we have
DF² = DE² + EF²
⇒ DF² = AB² + BC²         [∵  DE = AB and EF = BC         (By construction)]
⇒ DF² = AC²                        [∵  AB² + BC² = AC² (Given)]
⇒ DF = AC                              ….(i)
Thus, in  ∆ABC and  ∆DEF, we have
AB = DE, BC = EF           [By construction]
and, AC = DF                   [From equation (i)]
∴ ∆ABC ~ ∆DEF
⇒ ∠B = ∠E = 90º
Hence, ∆ABC is a right triangle right angled at B.

Pythagoras Theorem With Examples

Example 1:    Side of a triangle is given, determine it is a right triangle.
(2a – 1) cm, \(2\sqrt { 2a } \) cm,  and (2a + 1) cm
Sol.    Let p = (2a – 1) cm, q = \(2\sqrt { 2a } \) cm and r = (2a + 1) cm.
Then, (p² + q²) = (2a – 1)² cm² + (2 )² cm²
= {(4a² + 1– 4a) + 8a}cm²
= (4a² + 4a + 1)cm²
= (2a + 1)² cm² = r².
(p² + q²) = r².
Hence, the given triangle is right angled.

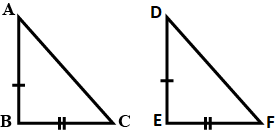
Example 2:    A man goes 10 m due east and then 24 m due north. Find the distance from the starting point.
Sol.    Let the initial position of the man be O and his final position be B. Since the man goes   10 m due east and then 24 m due north. Therefore, ∆AOB is a right triangle right-angled at A such that OA = 10 m and AB = 24 m.

By Phythagoras theorem, we have
OB² = OA² + AB²
⇒ OB² = 10² + 24² = 100 + 576 = 676
⇒ OB = \(\sqrt { 676 } \) = 26 m
Hence, the man is at a distance of 26 m from the starting point.

Example 3:    Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops.
Sol.

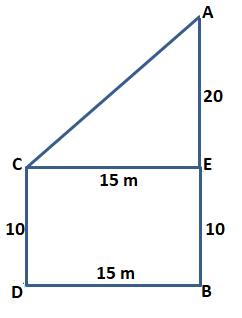
By Phythagoras theorem, we have
AC² = CE² + AE²
⇒ AC² = 15² + 20² = 225 + 400 = 625
⇒ AC = \(\sqrt { 625 } \) = 25 m.

Example 4:     In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that
AC² = AB² + BC² + 2BC × BD
Sol.    Given: An obtuse triangle ABC, obtuse-angled at B and AD is perpendicular to CB produced.
To Prove: AC² = AB² + BC² + 2BC × BD
Proof: Since ∆ADB is a right triangle right angled at D. Therefore, by Pythagoras theorem, we have AB² = AD² + DB²              ….(i)

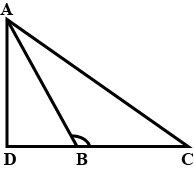
Again ∆ADC is a right triangle right angled at D.
Therefore, by Phythagoras theorem, we have
AC² = AD² + DC²
⇒ AC² = AD² + (DB + BC)²
⇒ AC² = AD² + DB² + BC² + 2BC • BD
⇒ AC² = AB² + BC² + 2BC • BD            [Using (i)]
Hence, AC² = AB² + BC² + 2BC • BD

Example 5:     In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that
AC² = AB² + BC² – 2BC × BD
Sol.    Given: A ∆ABC in which ∠B is an acute angle and AD ⊥ BC.
To Prove: AC² = AB² + BC² – 2BC × BD.
Proof: Since ∆ADB is a right triangle right-angled at D. So, by Pythagoras theorem, we have
AB² = AD² + BD²          ….(i)
Again ∆ADC is a right triangle right angled at D.

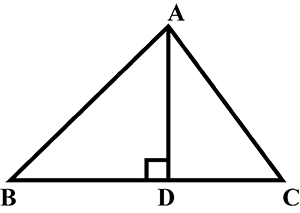
So, by Pythagoras theorem, we have
AC² = AD² + DC²
⇒ AC² = AD² + (BC – BD)²
⇒ AC² = AD² + (BC² + BD² – 2BC • BD)
⇒ AC² = (AD² + BD²) + BC² – 2BC • BD
⇒ AC² = AB² + BC² – 2BC • BD            [Using (i)]
Hence, AC² = AB² + BC² – 2BC • BD

Example 6:     If ABC is an equilateral triangle of side a, prove that its altitude = \(\frac { \sqrt { 3 }  }{ 2 } a\).
Sol.    ∆ABD is an equilateral triangle.
We are given that AB = BC = CA = a.
AD is the altitude, i.e., AD ⊥ BC.
Now, in right angled triangles ABD and ACD, we have
AB = AC                  (Given)
and AD = AD         (Common side)
∆ABD ≅ ∆ACD     (By RHS congruence)
⇒ BD = CD ⇒ BD = DC = \(\frac { 1 }{ 2 }BC\) = \(\frac { a }{ 2 }\)

From right triangle ABD.
AB² = AD² + BD²
\(\Rightarrow {{a}^{2}}=A{{D}^{2}}+{{\left( \frac{a}{2} \right)}^{2}} \)
\(\Rightarrow A{{D}^{2}}={{a}^{2}}-\frac{{{a}^{2}}}{4}=\frac{3}{4}{{a}^{2}}\)
\(\Rightarrow AD=\frac{\sqrt{3}}{2}a \)

Example 7:     ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle.
Sol.    Given that ∆ABC is right angled at A.
AC = 5 cm and AB = 12 cm
BC² = AC² + AB² = 25 + 144 = 169
BC = 13 cm
Join OA, OB, OC

Let the radius of the inscribed circle be r
Area of ∆ABC = Area of ∆OAB + Area of ∆OBC + Area of ∆OCA
⇒ 1/2 × AB × AC
\(=\frac{1}{2}\left( 12\text{ }\times \text{ }r \right)\text{ }+\frac{1}{2}\left( 13\text{ }\times \text{ }r \right)\text{ }+\frac{1}{2}\left( 5\text{ }\times \text{ }r \right)\)
⇒  12 × 5 = r × {12 + 13 + 5}
⇒  60 = r × 30 ⇒   r = 2 cm

Example 7:     ABCD is a rhombus. Prove that
AB² + BC² + CD² + DA² = AC² + BD²
Sol.    Let the diagonals AC and BD of rhombus ABCD intersect at O.
Since the diagonals of a rhombus bisect each other at right angles.
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90º
and AO = CO, BO = OD.
Since ∆AOB is a right triangle right-angle at O.

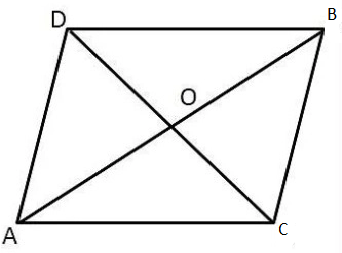
∴ AB² = OA² + OB²
\(\Rightarrow A{{B}^{2}}={{\left( \frac{1}{2}AC \right)}^{2}}+{{\left( \frac{1}{2}BD \right)}^{2}}\)         [∵ OA = OC and OB = OD]
⇒ 4AB² = AC² + BD²                      ….(i)
Similarly, we have
4BC² = AC² + BD²                    ….(ii)
4CD² = AC² + BD²                    ….(iii)
and, 4AD² = AC² + BD²           ….(iv)
Adding all these results, we get
4(AB² + BC² + AD²) = 4(AC² + BD²)
⇒ AB² + BC² + AD² + DA² = AC² + BD²

Example 8:     P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
(i) 4AQ² = 4AC² + BC²
(ii) 4BP² = 4BC² + AC²
(iii) (4AQ² + BP²) = 5AB²
Sol.    

(i)  Since ∆AQC is a right triangle right-angled at C.
∴ AQ² = AC² + QC²
⇒ 4AQ² = 4AC² + 4QC²         [Multiplying both sides by 4]
⇒ 4AQ² = 4AC² + (2QC)²
⇒ 4AQ² = 4AC² + BC² [∵  BC = 2QC]
(ii)  Since ∆BPC is a right triangle right-angled at C.
∴ BP² = BC² + CP²
⇒ 4BP² = 4BC² + 4CP²      [Multiplying both sides by 4]
⇒ 4BP² = 4BC² + (2CP)²
⇒ 4BP² = 4BC² + AC² [∵  AC = 2CP]
(iii)  From (i) and (ii), we have
4AQ² = 4AC² + BC² and, 4BC² = 4BC² + AC²
∴ 4AQ² + 4BP² = (4AC² + BC²) + (4BC² + AC²)
⇒ 4(AQ² + BP²) = 5 (AC² + BC²)
⇒ 4(AQ² + BP²) = 5 AB²
[In ∆ABC, we have AB² = AC² + BC²]

Example 9:     From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that :
(i) AF² + BD² + CE² = OA² + OB² + OC² – OD² – OE² – OF²
(ii) AF² + BD² + CE² = AE² + CD² + BF²
Sol.     

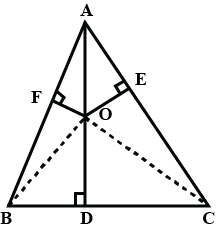
Let O be a point in the interior of ∆ABC and let OD ⊥ BC, OE ⊥ CA and OF ⊥ AB.
(i)  In right triangles ∆OFA, ∆ODB and ∆OEC, we have
OA² = AF² + OF²
OB² = BD² + OD²
and, OC² = CE² + OE²
Adding all these results, we get
OA² + OB² + OC² = AF² + BD² + CE² + OF² + OD² + OE²
⇒ AF² + BD² + CE² = OA² + OB² + OC² – OD² – OE² – OF²
(ii)  In right triangles ∆ODB and ∆ODC, we have
OB² = OD² + BD²
and, OC² = OD² + CD²
OB² – OC² = (OD² + BD²) – (OD² + CD²)
⇒ OB² – OC² = BD² – CD²        ….(i)
Similarity, we have
OC² – OA² = CE² – AE²             ….(ii)
and, OA² – OB² = AF² – BF²            ….(iii)
Adding (i), (ii) and (iii), we get
(OB² – OC²) + (OC² – OA²) + (OA² – OB²)
= (BD² – CD²) + (CE² – AE²) + (AF² – BF²)
⇒ (BD² + CE² + AF²) – (AE² + CD² + BF²) = 0
⇒ AF² + BD² + CE² = AE² + CD² + BF²

Example 10:     In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
(i) 9 AQ² = 9 AC² + 4 BC²
(ii) 9 BP² = 9 BC² + 4 AC²
(iii) 9 (AQ² + BP²) = 13 AB²
Sol.    It is given that P divides CA in the ratio 2 : 1. Therefore,
\(CP=\frac { 2 }{ 3 }AC\)      ….(i)
Also, Q divides CB in the ratio 2 : 1.
∴ \(QC=\frac { 2 }{ 3 }BC\)      ….(ii)

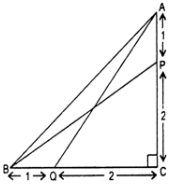
(i)  Applying pythagoras theorem in right-angled triangle ACQ, we have
AQ² = QC² + AC²
⇒ AQ² = \(\frac { 4 }{ 9 }\) BC² + AC²              [Using (ii)]
⇒ 9 AQ² = 4 BC² + 9 AC²            ….(iii)
(ii)  Applying pythagoras theorem in right triangle BCP, we have
BP² = BC² + CP²
⇒ BP² = BC² + AC²               [Using (i)]
⇒ 9 BP² = 9 BC² + 4 AC²             ….(iv)
(iii)  Adding (iii) and (iv), we get
9 (AQ² + BP²) = 13 (BC² + AC²)
⇒ 9 (AQ² + BP²) = 13 AB² [∵  BC² = AC² + AB²]

Example 11:     In a ∆ABC, AD ⊥ BC and AD² = BC × CD. Prove ∆ABC is a right triangle.
Sol.    

In right triangles ADB and ADC, we have
AB² = AD² + BD²             ….(i)
and, AC² = AD² + DC²           ….(ii)
Adding (i) and (ii), we get
AB² + AC² = 2 AD² × BD² + DC²
⇒ AB² + AC² = 2BD × CD + BD² + DC²         [∵  AD² = BD × CD (Given)]
⇒ AB² + AC² = (BD + CD)² = BC²
Thus, in ∆ABC, we have
AB² = AC² + BC²
Hence, ∆ABC, is a right triangle right-angled at A.

Example 12:      The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that 2AB² = 2AC² + BC².
Sol.    We have,

DB = 3CD
BC = BD + DC
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that
2AC2 + BC2.
We have,
DB = 3CD
∴ BC = BD + DC
⇒ BC = 3 CD + CD
⇒ BD = 4 CD ⇒  CD = \(\frac { 1 }{ 4 }\) BC
∴ CD = \(\frac { 1 }{ 4 }\) BC  and BD = 3CD = \(\frac { 1 }{ 4 }\) BC           ….(i)
Since ∆ABD is a right triangle right-angled at D.
∴ AB² = AD² + BD²           ….(ii)
Similarly, ∆ACD is a right triangle right angled at D.
∴ AC² = AD² + CD²         ….(iii)
Subtracting equation (iii) from equation (ii)  we get
AB² – AC² = BD² – CD²
⇒ AB² – AC² = \({{\left( \frac{3}{4}BC \right)}^{2}}-{{\left( \frac{1}{4}BC \right)}^{2}}\)       \(\left[ From\ (i)\ CD=\frac{1}{4}BC,\ BD=\frac{3}{4}BC \right]\)
⇒ AB² – AC² = \(\frac { 9 }{ 16 }\) BC² – \(\frac { 1 }{ 16 }\) BC²
⇒ AB² – AC² = \(\frac { 1 }{ 2 }\) BC²
⇒ 2(AB² – AC²) = BC²
⇒ 2AB² = 2AC² + BC².

Example 13:      ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
(ii) \(\frac{1}{{{p}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}\)
Sol.    (i)  Let CD ⊥ AB. Then, CD = p.

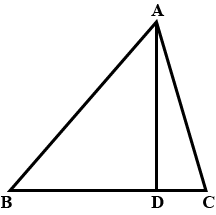
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) (Base × Height)
⇒  Area of ∆ABC = \(\frac { 1 }{ 2 }\) (AB × CD) =  \(\frac { 1 }{ 2 }\) cp
Also,
Area of ∆ABC = \(\frac { 1 }{ 2 }\) (BC × AC) = \(\frac { 1 }{ 2 }\) ab
∴ \(\frac { 1 }{ 2 }\) cp = \(\frac { 1 }{ 2 }\) ab
⇒  cp = ab
(ii)  Since ∆ABC is right triangle right-angled at C.
∴ AB² = BC² + AC²
⇒  c² = a² + b²
\(\Rightarrow {{\left( \frac{ab}{p} \right)}^{2}}={{a}^{2}}+{{b}^{2}} \)         \(\left[ \because \ cp\,=\,ab\ \ \therefore c=\frac{ab}{p} \right]\)
\(\Rightarrow \frac{{{a}^{2}}{{b}^{2}}}{{{p}^{2}}}={{a}^{2}}+{{b}^{2}} \)
\(\Rightarrow \frac{1}{{{p}^{2}}}=\frac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}{{b}^{2}}}\Rightarrow \frac{1}{{{p}^{2}}}=\frac{1}{{{b}^{2}}}+\frac{1}{{{a}^{2}}} \)
\(\Rightarrow \frac{1}{{{p}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}} \)