Differential Equations
An equation involving independent variable x, dependent variable y and the differential coefficients \(\frac { dy }{ dx } ,\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } ,…..\) is called differential equation.
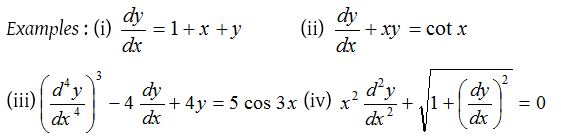
(1) Order of a differential equation:
The order of a differential equation is the order of the highest derivative occurring in the differential equation. For example, the order of above differential equations are 1,1,4 and 2 respectively.
The order of a differential equation is a positive integer. To determine the order of a differential equation, it is not needed to make the equation free from radicals.
(2) Degree of a differential equation:
The degree of a differential equation is the degree of the highest order derivative, when differential coefficients are made free from radicals and fractions. The degree of above differential equations are 1, 1, 3 and 2 respectively.
Formation of differential equation
Formulating a differential equation from a given equation representing a family of curves means finding a differential equation whose solution is the given equation. The equation so obtained is the differential equation of order n for the family of given curves.
Algorithm for formation of differential equations
Step (i): Write the given equation involving independent variable x (say), dependent variable y (say) and the arbitrary constants.
Step (ii): Obtain the number of arbitrary constants in step (i). Let there be n arbitrary constants.
Step (iii): Differentiate the relation in step (i) n times with respect to x.
Step (iv): Eliminate arbitrary constants with the help of n equations involving differential coefficients obtained in step (iii) and an equation in step (i). The equation so obtained is the desired differential equation.
Variable separable type differential equation
(1) Equations in variable separable form:
If the differential equation of the form f1(x) dx = f2(y) dy …..(i)
where f1 and f2 being functions of x and y only. Then we say that the variables are separable in the differential equation.
Thus, integrating both sides of (i), we get its solution as ∫f1(x) dx = ∫f2(y) dy + c, where c is an arbitrary constant.
There is no need of introducing arbitrary constants to both sides as they can be combined together to give just one.
(2) Equations reducible to variable separable form:
(i) Differential equations of the form \(\frac { dy }{ dx } =f(ax+by+c)\) can be reduced to variable separable form by the substitution ax + by + c = Z.
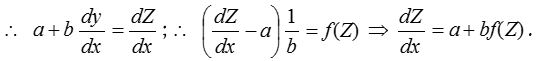
(ii) Differential equation of the form
This is variable separable form and can be solved.
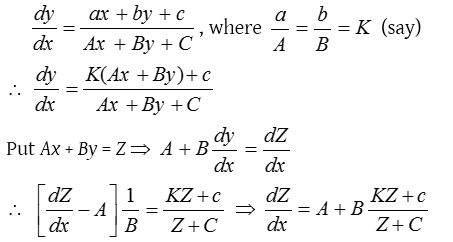
Homogeneous differential equation
Exact differential equation
(1) Exact differential equation:
If M and N are functions of x and y, the equation Mdx + Ndy = 0 is called exact when there exists a function f(x, y) of x and y such that
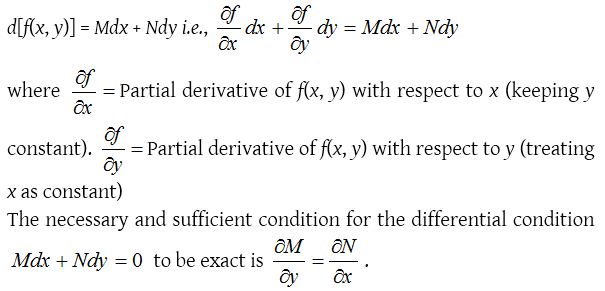
An exact differential equation can always be derived from its general solution directly by differentiation without any subsequent multiplication, elimination etc.
(2) Integrating factor:
If an equation of the form Mdx + Ndy = 0 is not exact, it can always be made exact by multiplying by some function of x and y. Such a multiplier is called an integrating factor.
(3) Working rule for solving an exact differential equation:
Step (i): Compare the given equation with Mdx + Ndy = 0 and find out M and N.
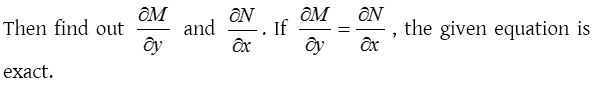
Step (ii): Integrate M with respect to x treating y as a constant.
Step (iii): Integrate N with respect to y treating x as constant and omit those terms which have been already obtained by integrating M.
Step (iv): On adding the terms obtained in steps (ii) and (iii) and equating to an arbitrary constant, we get the required solution.
In other words, solution of an exact differential equation is
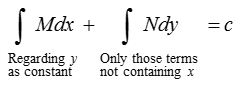
Solution by inspection
If we can write the differential equation in the form f(f1(x))d(f1(x, y)) + ϕ(f2(x))d(f2(x, y)) + ………. = 0, then each term can be easily integrated separately. For this the following results must be memorized.
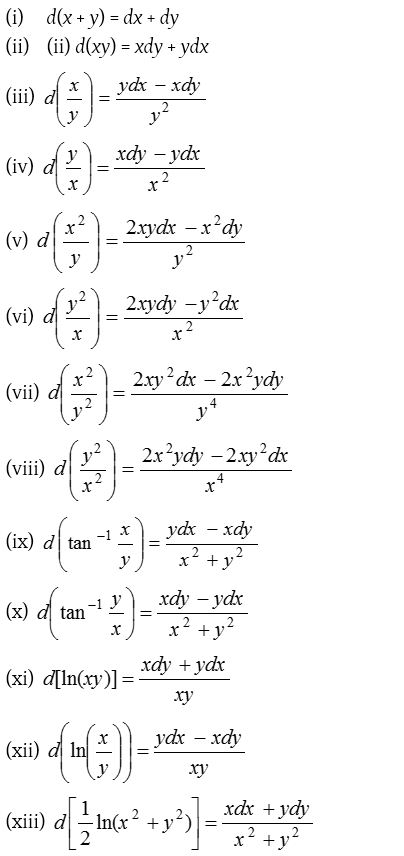
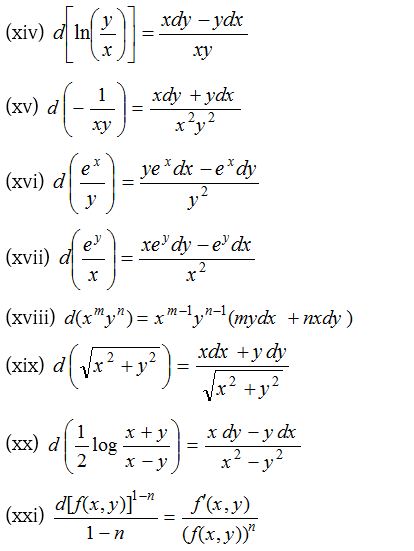
Linear differential equation
Application of differential equation
Differential equation is applied in various practical fields of life. It is used to define various physical laws and quantities. It is widely used in physics, chemistry, engineering etc.
Some important fields of application are:
(i) Rate of change (ii) Geometrical problems etc.
Miscellaneous differential equation
A special type of second order differential equation:
