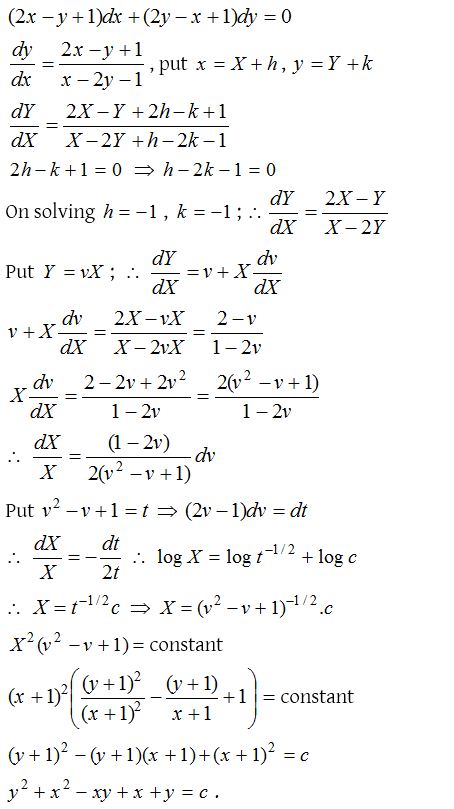Homogeneous Differential Equations
Homogeneous differential equation
A function f(x,y) is called a homogeneous function of degree if f(λx, λy) = λn f(x, y).
For example, f(x, y) = x2 – y2 + 3xy is a homogeneous function of degree 2.
A homogenous function of degree n can always be written as
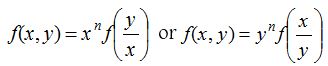
If a first-order first-degree differential equation is expressible in the form \(\frac { dy }{ dx } =\frac { f(x,y) }{ g(x,y) }\) where f(x, y) and g(x, y) are homogeneous functions of the same degree, then it is called a homogeneous differential equation. Such type of equations can be reduced to variable separable form by the substitution y = νx. The given differential equation can be written as
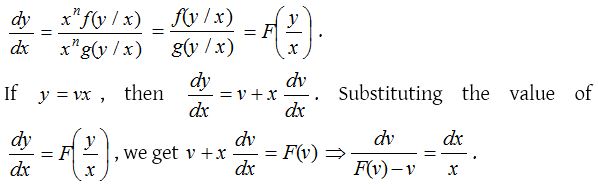
On integration, \(\int { \frac { 1 }{ F(v)-v } } dv\quad =\quad \int { \frac { dx }{ x } +c }\) where c is an arbitrary constant of integration. After integration, v will be replaced by \(\frac { y }{ x }\) in complete solution.
Equation reducible to homogeneous form
A first order, first degree differential equation of the form
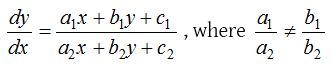
This is non-homogeneous.
It can be reduced to homogeneous form by certain substitutions. Put x = X + h, y = Y + k.
Where h and k are constants, which are to be determined.
Homogeneous Differential Equations Problems with Solutions
1.

Solution:

2.
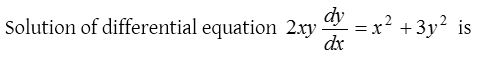
Solution:
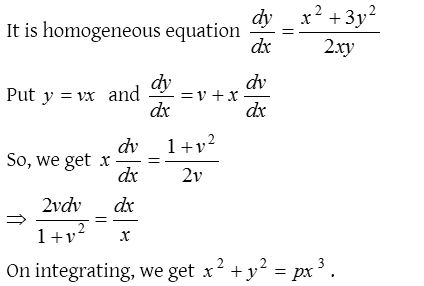
3.
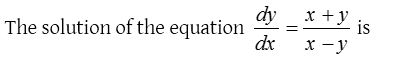
Solution:

4.
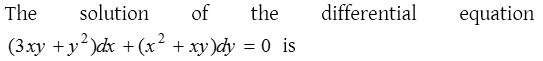
Solution:

5.
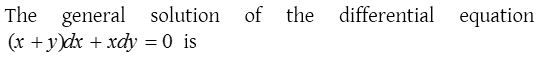
Solution:
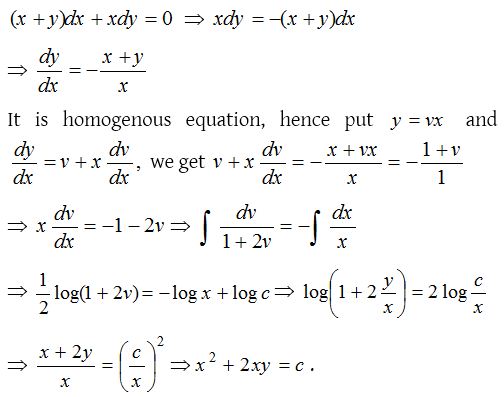
6.

Solution:
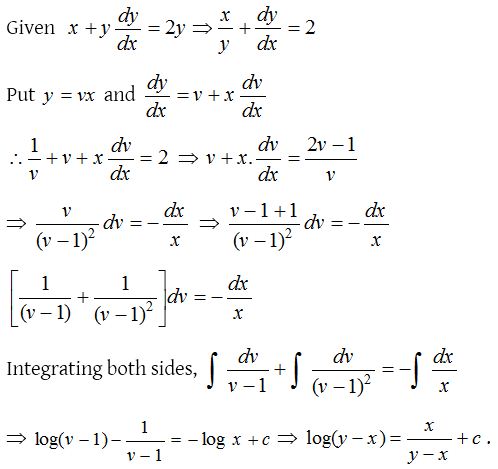
7.

Solution:
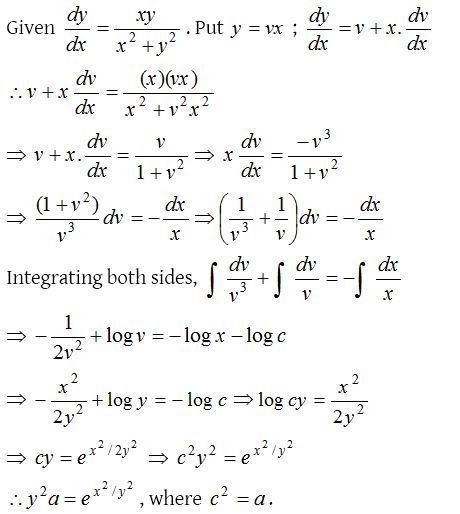
8.
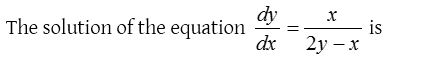
Solution:
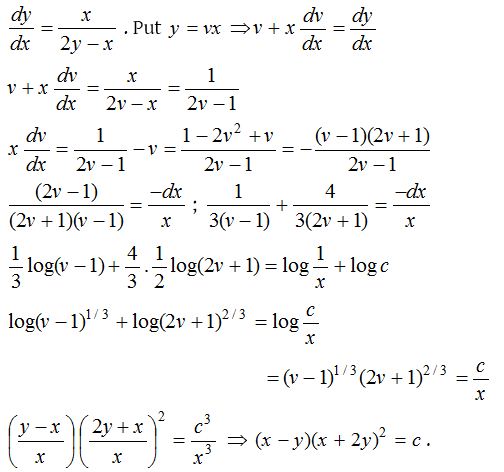
9.
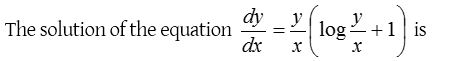
Solution:
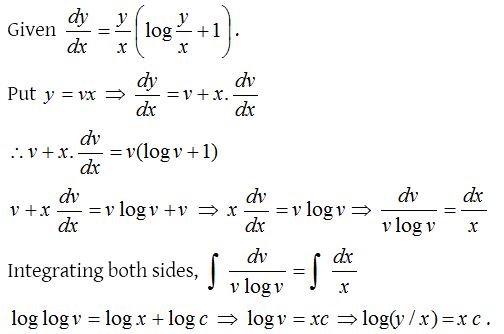
10.
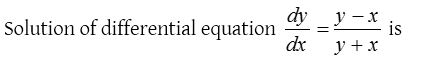
Solution:
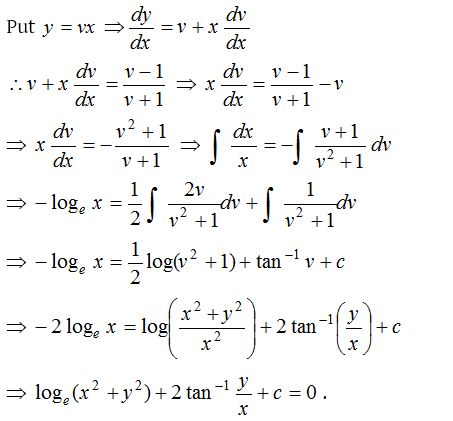
11.
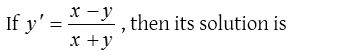
Solution:

12.
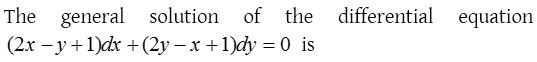
Solution: