Decimal Representation Of Rational Numbers

Decimal Representation Of Rational Numbers

Example 1:    Express $\frac { 7 }{ 8 }$ in the decimal form by long division method.
Solution:    We have,

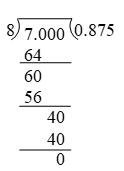
∴ $\frac { 7 }{ 8 }$ = 0.875

Example 2:    Convert $\frac { 35 }{ 16 }$ into decimal form by long division  method.
Solution:    We have,  

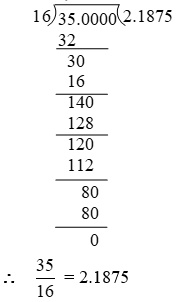
Example 3:    Express $\frac { 2157 }{ 625 }$ in the decimal form.
Solution:    We have,

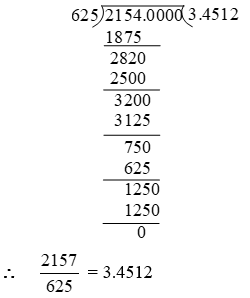
Example 4:    Express $\frac { -17 }{ 8 }$ in decimal form by long division method.
Solution:    In order to convert $\frac { -17 }{ 8 }$ in the decimal form, we first express $\frac { 17 }{ 8 }$ in the decimal form and the decimal form of $\frac { -17 }{ 8 }$ will be negative of the decimal form of $\frac { 17 }{ 8 }$
we have,

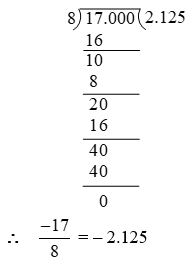
Example 5:    Find the decimal representation of $\frac { 8 }{ 3 }$ .
Solution:    By long division, we have

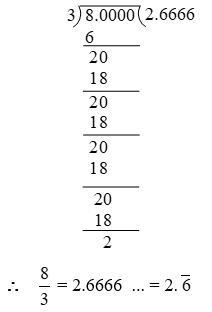
Example 6:    Express $\frac { 2 }{ 11 }$ as a decimal fraction.
Solution:    By long division, we have

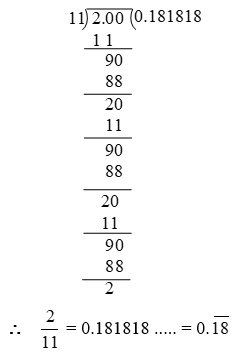
Example 7:    Find the decimal representation of $\frac { -16 }{ 45 }$
Solution:    By long division, we have

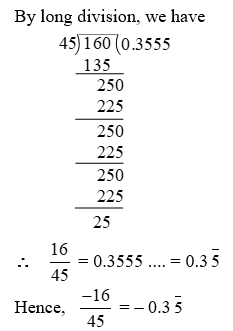
Example 8:    Find the decimal representation of $\frac { 22 }{ 7 }$
Solution:    By long division, we have


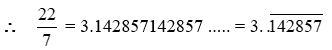
So division of rational number gives decimal expansion. This expansion represents two types
(A) Terminating (remainder = 0)

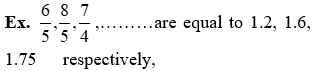
So these are terminating and non repeating (recurring)
(B) Non terminating recurring (repeating)
(remainder ≠ 0, but equal to devidend)

These expansion are not finished but digits are continusely repeated so we use a line on those digits, called bar $(\bar{a})$.
So we can say that rational numbers are of the form either terminating, non repeating or non terminating repeating (recurring).

Maths