Absolute Value Equations
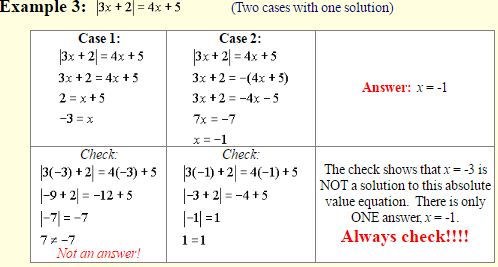
To solve an absolute value equation, isolate the absolute value on one side of the equal sign, and establish two cases:
Case 1:
|a| = b set a = b
Set the expression inside the absolute value symbol equal to the other given expression.
Case 2:
|a| = b set a = – b
Set the expression inside the absolute value symbol equal to the negation of the other given expression.

Always Check your answers.
The two cases create “derived” equations. These derived equations may not always be true equivalents to the original equation. Consequently, the roots of the derived equations MUST BE CHECKED in the original equation so that you do not list extraneous roots as answers.

Read More:
- Absolute Value
- Absolute Value Inequalities
- Absolute Value of Complex Numbers
- Integers and Examples
- Fundamental Operations on Integers
- Whole Numbers And Its Properties
- Hints for Remembering the Properties of Real Numbers
- What Are The Four Basic Operations In Mathematics
- Order of Operations and Evaluating Expressions
Example 2: (No solution)
As soon as you isolate the absolute value expression, you observe:
There is no need to work out the two cases in this problem. Absolute value is NEVER equal to a negative value. This equation is never true. The answer is the empty set .
Example 4: A machine fills Quaker Oatmeal containers with 32 ounces of oatmeal. After the containers are filled, another machine weighs them. If the container’s weight differs from the desired 32 ounce weight by more than 0.5 ounces, the container is rejected. Write an equation that can be used to find the heaviest and lightest acceptable weights for the Quaker Oatmeal container. Solve the equation.
