Base Quantities and Derived Quantities Definition, Units Examples

Base Quantities and Derived Quantities Definition, Units Examples

1. Physical quantities are quantities that can be measured.
2. Usually, a specific scientific instrument is used to measure a particular physical quantity.
   
3. To describe a physical quantity we first define the unit in which the measurement is made. There are many systems of units but the most common system of units used by scientists is based on the metric system.
4. The modernised version of the metric system is called International System of Units, officially abbreviated as SI.
5. We can represent a physical quantity by the symbol of the quantity, the numerical value of the magnitude of the quantity and the unit of measurement of the quantity. For example, Figure shows a footballer scoring a goal. The ball was kicked a distance of 8 m.
   
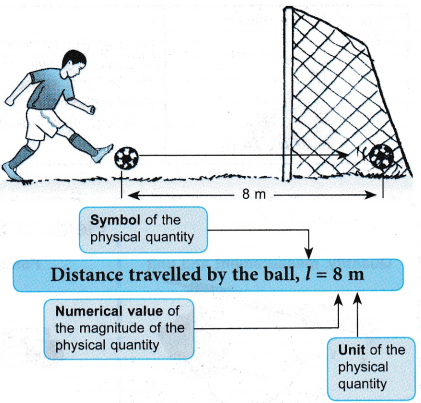
6. There are two types of physical quantities, that is, base quantities and derived quantities.
7. Base quantities are physical quantities that cannot be defined in terms of other quantities. Table shows five base quantities and their respective SI units.
   

   Base quantity	Symbol	SI unit	Symbol of SI unit
   Length	l	meter	m
   Mass	m	kilogram	kg
   Time	t	second	S
   Temperature	T	kelvin	K
   Electric current	I	ampere	A

   Derived quantities are physical quantities derived from combinations of base quantities through multiplication.

8. Table shows some derived quantities and their respective derived units.
9. 

Example 1
It was already noon when Lela woke up. The temperature was 38°C and she was sweating all over. As it was already late, she was given only 10 minutes to pack her things. She wondered how she would pack a 1.5 kg tin of milk powder, 850 cm³ of lake water, 980 g of a rare rock, a 1.2 m long stem of a special plant and finally not to forget 6.5 m² of tent material into her bag.

From the above description, identify the physical quantities and then classify them into base quantities and derived quantities.
Solution:
The physical quantities are temperature (38°C), time (10 minutes), mass (1.5 kg and 980 g), length (1.2 m), volume (850 cm³) and area (6.5 m²).
Classification:
Base quantity: Mass, length, temperature, time
Derived quantity: Area, volume v

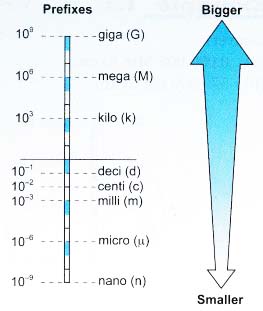
Prefixes

1. Prefixes are used to simplify the description of physical quantities that are either very big or very small in SI units.
2. Table lists some commonly used SI prefixes and their multiplication factors.
   

   Prefix	Symbol	Value
   pico	P	10-12
   nano	n	10-9
   micro	p	10-6
   milli	m	10-3
   centi	c	10-2
   deci	d	10-1
   kilo	k	103
   mega	M	106
   giga	G	109
   tera	T	1012

Example 2
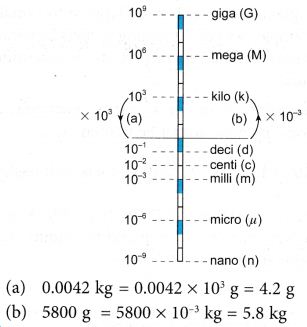
It is difficult for Hawa to figure out the mass of a piece of paper which is 0.0042 kg and the mass of a cat which is 5800 g. To simplify the description of these physical quantities, prefixes are used.
Please help Hawa to express
(a) 0.0042 kg in g,
(b) 5800 g in kg.
Solution:

Example 3
Convert
(a) 0.000 006 Mm to cm,
(b) 570 000 cm to km.

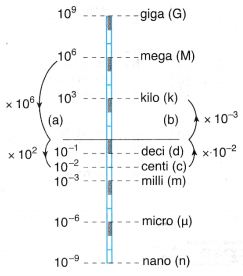
Solution:

Scientific Notation

1. The distance of Pluto from the Earth is about 6 000 000 000 000 m and the radius of a hydrogen atom is about 0.000 000 000 05 m. These quantities are either too large or too small and a simpler way of expressing them is by using standard form of representation or scientific notation.
2. In a standard form or scientific notation, a numerical magnitude can be written as:
   A × 10ⁿ, where 1 ≤ A < 10 and n is an integer
   Hence, the distance of Pluto from the Earth can be written as 6 × 10¹² m and the radius of a hydrogen atom as 5 × 10^-11 m.
   

Example 4
For each of the following, express the magnitude using scientific notation.
(a) The length of a virus = 0.000 000 08 m
(b) The mass of a ship = 75 000 000 kg
Solution:

Conversion of Units Involving Derived Quantities

When converting the units of a derived quantity, each of its base units involved must be converted. The following Example illustrates the conversion of derived units.
Example 5
Convert each of the following from one particular unit to another and represent the quantity in standard form.
(a) Convert the area of a button from 1.2 cm² into m².
(b) Convert the volume of a water tank from 2.5 m³ into cm³.
(c) Convert the density of mercury from 13.6 g cm^-3 into kg m^-3.
Solution: