ICSE Solutions for Class 10 Mathematics – Solving Linear Inequations in One Variable

ICSE Solutions for Class 10 Mathematics – Solving Linear Inequations in One Variable

ICSE SolutionsSelina ICSE Solutions

Get ICSE Solutions for Class 10 Mathematics Chapter 5 Linear Inequations (Solving Linear Inequations in One Variable) for ICSE Board Examinations on APlusTopper.com. We provide step by step Solutions for ICSE Mathematics Class 10 Solutions Pdf. You can download the Class 10 Maths ICSE Textbook Solutions with Free PDF download option.

Download Formulae Handbook For ICSE Class 9 and 10

Formulae

Two permissible rules:

1. Addition – Subtraction Rule:
   If the same number or expression is added to or subtracted from both sides of an inequation, the resulting inequation has the same solution (or solutions) as the original.
2. Multiplication – Division Rule:
   (i) If both sides of an inequation are multiplied or divided by the same positive number, the resulting inequation has the same solution (or solutions) as the original.
   (ii) If both sides of an inequation are multiplied or divided by the same negative number, the resulting inequation has the same solution (or solutions) as the original if the symbol of the inequality is reversed.
   Thus, the only difference between solving a linear equation and solving an inequation concerns multiplying or dividing both sides by a negative number. Therefore, always reverse the symbol of an inequation when multiplying or dividing by a negative number.
3. Properties of absolute values:
   
   

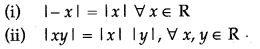
Determine the Following

Question 1. Give that x ∈ I. Solve the inequation and graph the solution on the number line:

Question 2. Graph the solution set for each inequality:


Question 3. Solve the given inequation and graph the solution on the number line

Question 4. Given that x ∈ R, solve the following inequality and graph the solution on the number line:

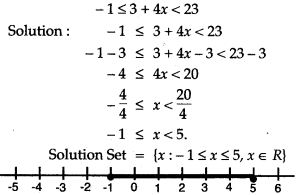
Question 5. Given:

Question 6. Solve 2 ≤ 2x – 3 ≤ 5, x ∈ R and mark it on a number line.

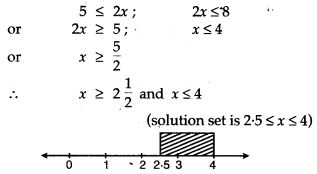
Question 7. For each inequality, determine which of the given numbers are in the solution set:

Question 8. Graph the solution sets of the following inequalities:

Question 9. Solve the equation and represent the solution set on the number line.

Question 10. Solve the following inequation and represent the solution set on the number line:

Question 11. Solve the following in equalities and graph their solution set

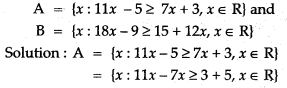
Question 12. Solve the following inequation and graph the solution set,

Question 13. Solve the following inequation and graph the solution on the number line.

Question 14. Solve the following inequalities and represent the solution on a number line:

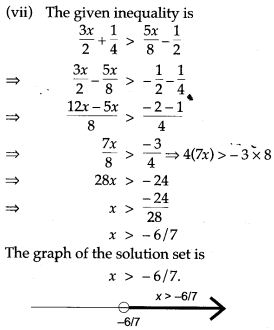
Question 15. Solve the following inequalities and represent the solution set on a number line:

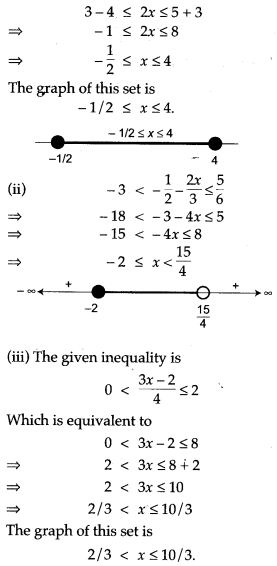
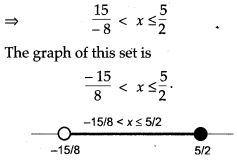
Question 16. Solve the following inequation, write the solution set and represent it on the number line:

Question 17. Find the values of x, which satisfy the inequation

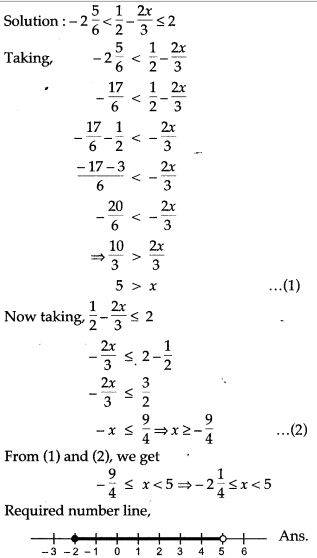
Question 18. Solve the following inequalities in the given universal set:

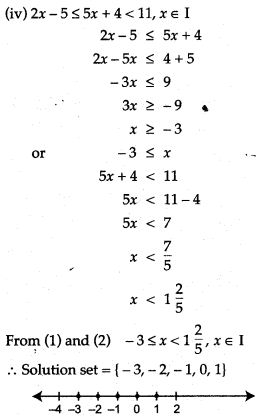
Question 19. Find the solution set of the following inequalities and draw the graph of their solutions sets:

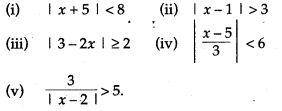
Question 20. Solve the following inequalities and graph their solution set:

For More Resources