Solution Of A Linear Equation In Two Variables Example Problems With Solutions
Method: Put the value of x (or y) = 0, ±1, ±2, ±3,……, we get values of y (or x). By this we can find many solutions of given equation.
Read More:
- What is a Linear Equation
- Linear Equations In One Variable
- Graphical Method Of Solving Linear Equations In Two Variables
- RS Aggarwal Class 10 Solutions Linear Equations In Two Variables
- RS Aggarwal Class 9 Solutions Linear Equations In Two Variables
- RS Aggarwal Class 8 Solutions Linear Equations
- RS Aggarwal Class 7 Solutions Linear Equations in One Variable
- RS Aggarwal Class 6 Solutions Linear Equation In One Variable
https://www.youtube.com/watch?v=DWj-aRuMaJU
Example 1: Find five solutions of
(i) 2x + 3y = 6 (ii) 3x – 2y = 12 (iii) 7x + y = 15
Solution: (i) 2x = 6 – 3y
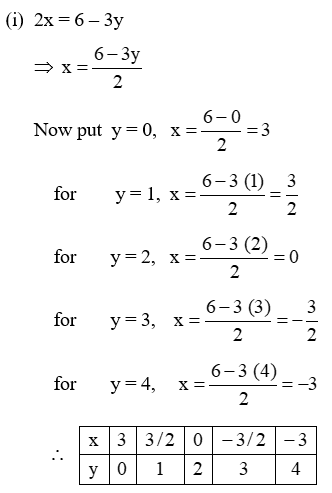
Example 2: Find two solutions of
(i) 3x – 7y = 21 (ii) 8x – 5y = 16
Solution: (i) 3x – 7y = 21
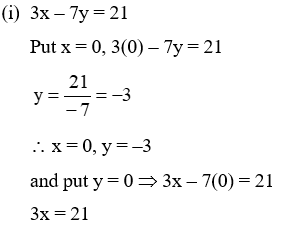
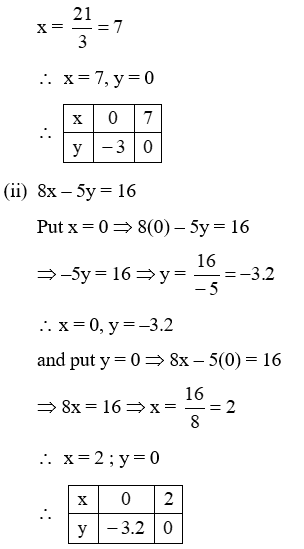
Example 3: Find five solutions of
(i) 3x = 5 (ii) 7y = 10
Solution: (i) The equation is only in one variable. So we have to convert into 2 variable 3x + 0.y = 5
Note:
Ordered Pair: If value of x & y are represent in form (x, y) then this form is called ordered pair form : Eg. x = 5, y = 7/3 then ordered pair form = (5, 7/3). First part is called abscissa (x part) and second part is ordinate (y part).
Example 4: Check the following value of x & y are solution of equation 9x – 8y = 72 or not
(i) (0, 9) (ii) (0, – 9) (iii) (– 8, 0)
(iv) (+8, 0) (v) (1, 1) (vi) (1/3, 1/2)
Solution: Given equation 9x – 8y = 72
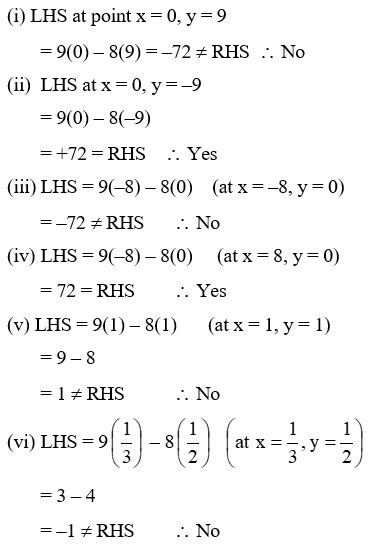
Example 5: Find the value of k in equation 2x + ky = 6 if (–2, 2) is a solution.
Solution: ∵ (–2, 2) is a solution of 2x + ky = 5
∴ 2(–2) + k(2) = 6
– 4 + 2k = 6 ⇒ 2k = 6 + 4
k = 10/2 = 5
Example 6: Find value of p if (4, –4) is a solution of x – py = 8.
Solution: x – py = 8
4 – p (–4) = 8
4p = 8 – 4
4p = 4
p = 1
Example 7: Find the value of a if (a, –3a) is a solution of 14x + 3y = 35.
Solution: Put x = a and y = –3a in given equation
14(a) + 3(–3a) = 35
14a – 9a = 35
5a = 35
a = 7