ICSE Solutions for Class 10 Mathematics - Similarity

ICSE Solutions for Class 10 Mathematics – Similarity

ICSE SolutionsSelina ICSE Solutions

Get ICSE Solutions for Class 10 Mathematics Chapter 13 Similarity for ICSE Board Examinations on APlusTopper.com. We provide step by step Solutions for ICSE Mathematics Class 10 Solutions Pdf. You can download the Class 10 Maths ICSE Textbook Solutions with Free PDF download option.

Download Formulae Handbook For ICSE Class 9 and 10

Formulae

Similarities of triangles: When two triangles are similar, their corresponding angles are equal and corresponding sides are proportional.

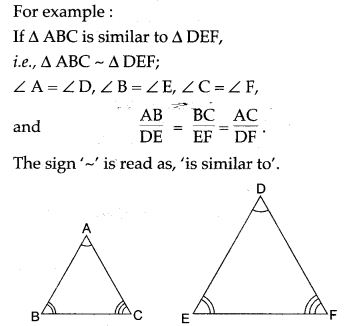
Axioms of similarity of triangles: (i.e., three similarity postulates for triangle)

1. If two triangles have a pair of corresponding angles equal and the sides including them proportional; then the triangles are similar (SAS postulate).
2. If two triangles have two pairs of corresponding angles equal; the triangles are similar (AA or AAA postulate).
3. If two triangles have their three pairs of corresponding sides proportional, the triangles are similar (SSS postulate).

Basic Theorem of Proportionality:

1. A line drawn parallel to any side of a triangle, divides the other two sides proportionally. (Basic proportionality theorem).
   
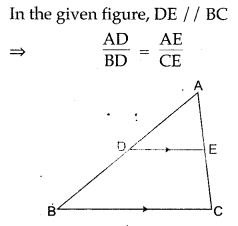
   Conversely: If a line divides two sides of a triangle proportionally, the line is parallel to the third side.
   
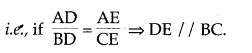
2. Relation between the areas of two triangles: Theorem: The areas of two similar triangles are proportional to the squares on their corresponding sides.
   

Determine the Following

Question 1. The model of a building is constructed with scale factor 1:30.
(i) If the height of the model is 80 cm, find the actual height of the building in metres.
(ii) If the actual volume of a tank at the top of the building is 27 m³, find the volume of the tank on the top of the model.

Question 2. Triangles ABC and DEF are similar.

Prove the Following 

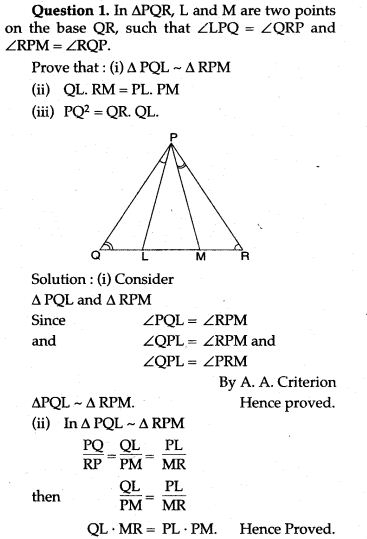
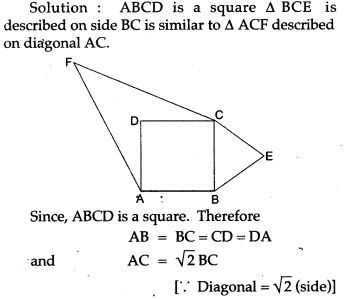
Question 3. Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.

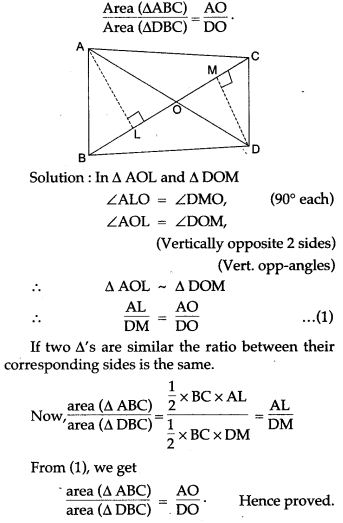
Question 4. In figure ABC and DBC are two triangles on the same base BC. Prove that

Question 5. In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that

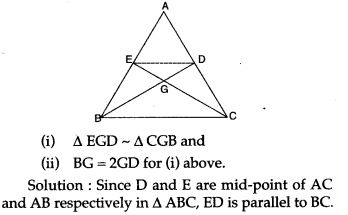
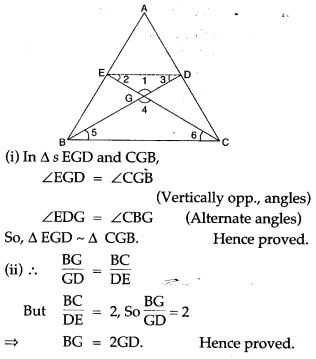
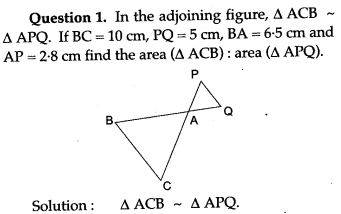
Figure Based Questions

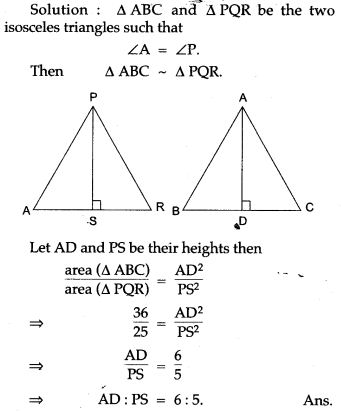
Question 2. Two isosceles triangle have equal vertical angles and their areas are in the ratio of 36 : 25. Find the ratio between their corresponding heights.

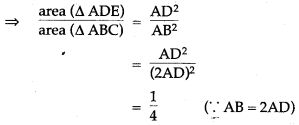
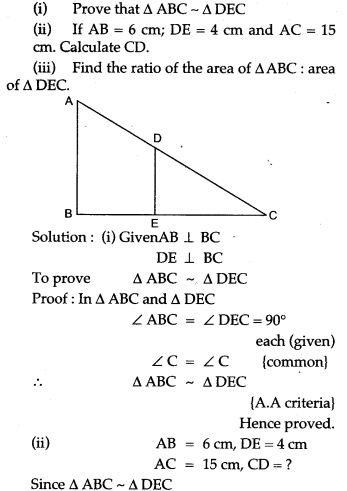
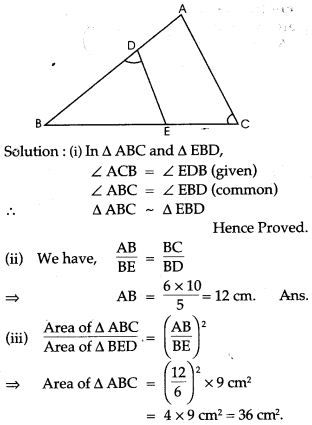
Question 4. In the given figure, AB and DE are perpendicular to BC.

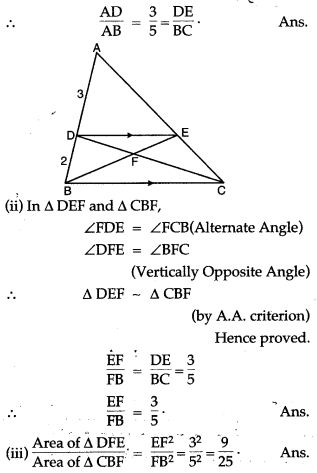
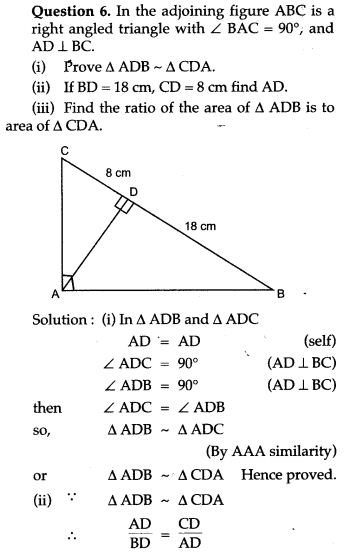
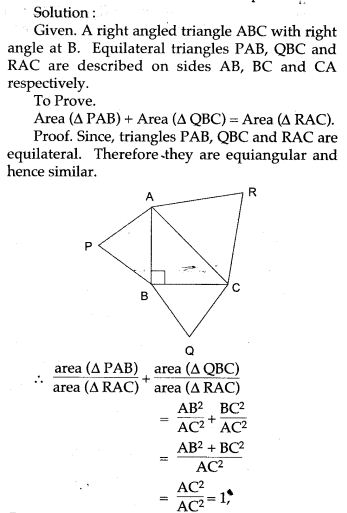
Question 7. Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.

Question 8: On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 90⁰ each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.

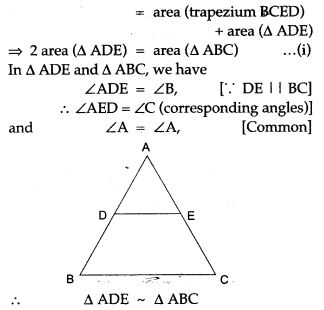
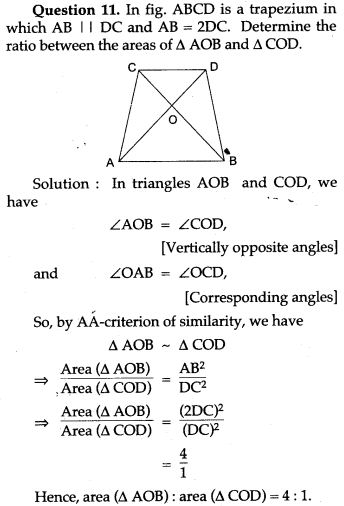
Question 10. In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.

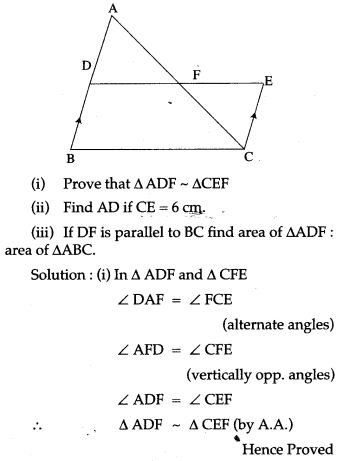
Question 14. In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF : AC = 5 : 8.

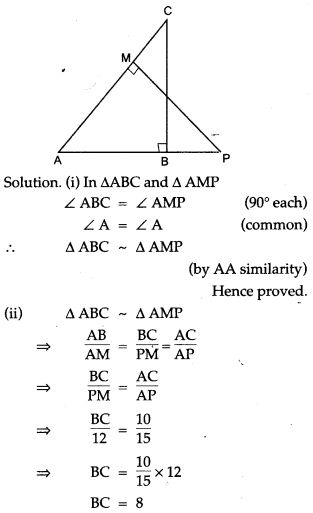
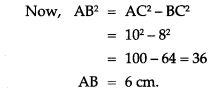
Question 16. Triangles ABC and DEF are similar.

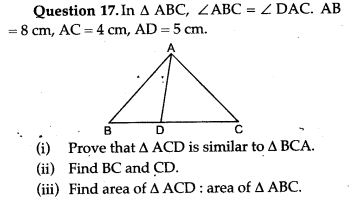
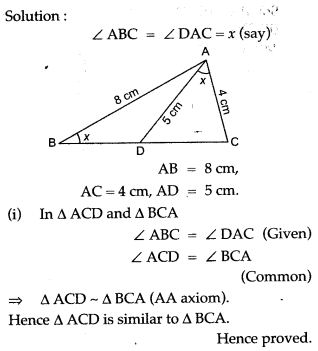
For More Resources