Selina Concise Physics Class 9 ICSE Solutions Laws of Motion

Selina Concise Physics Class 9 ICSE Solutions Laws of Motion

ICSE SolutionsSelina ICSE Solutions

APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 9 Physics Chapter 3 Laws of Motion. You can download the Selina Concise Physics ICSE Solutions for Class 9 with Free PDF download option. Selina Publishers Concise Physics for Class 9 ICSE Solutions all questions are solved and explained by expert teachers as per ICSE board guidelines.

Download Formulae Handbook For ICSE Class 9 and 10

Selina ICSE Solutions for Class 9 Physics Chapter 3 Laws of Motion

Exercise 3(A)

Solution 1S.

a. The forces which act on bodies when they are in physical contact are called contact forces.
Example: frictional force and force exerted on two bodies during collision.

b. The forces experienced by bodies even without being physically touched are called non-contact forces.
Example: Gravitational force and Electrostatic force.

Solution 2S.

Contact force: (a) frictional force (b) normal reaction force (c) force of tension in a string
Non-contact force: (d) gravitational force (e) electric force (f) magnetic force

Solution 3S.

a. Force exerted on two bodies during collision.
b. Magnetic force between magnetic poles.

Solution 4S.

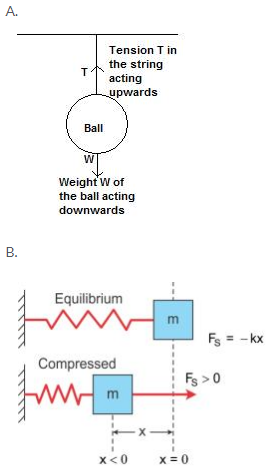
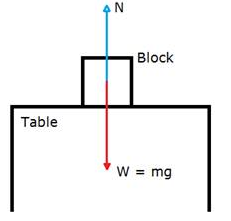
C. The forces acting on the block are its weight in the downward direction and the normal reaction force due to the table on the upward direction.

Solution 5S.

The magnitude of non-contact force on two bodies depends on the distance of separation between them.
The force decreases as the distance of separation increases.
The force is inversely proportional to the square of the distance of separation.

Solution 6S.

The magnitude of gravitational force between two masses will become four times as gravitational force varies inversely as the square of distance of separation.

Solution 7S.

A force when applied on a non-rigid body changes the inter-spacing between its constituent particles and therefore causes a change in its dimensions and can also produce motion in it.
On the other hand, a force when applied on a rigid body, does not change the inter-spacing between its constituent particles and therefore it does not change the dimensions of the body but causes motion in it

Solution 8S.

i. A fielder on the ground stops a moving ball by applying a force with his hands.
ii. The pull exerted by horse makes a cart moves.
iii. In a cycle pump, when the piston is lowered, the air is compressed to occupy a less volume.
iv. On pressing a piece of rubber, its shape changes.

Solution 1M.

Frictional force is a contact force.

Solution 2M.

Force due to gravity is a non-contact force.

Exercise 3(B)

Solution 1S.

Force causes motion in a body.

Solution 2S.

Force is not needed to keep a moving body in motion.

Solution 3S.

The force of friction between the table and the ball opposes the motion of the ball.

Solution 4S.

In absence of any external force, its speed shall remain unchanged.

Solution 5S.

Galileo’s law of inertia states that a body continues to be in its state of rest or of uniform motion unless an external force is applied on it.

Solution 6S.

According to Newton’s first law of motion, if a body is in a state of rest, it will remain in the state of rest, and if the body is in the state of motion, it will remain moving in the same direction with the same speed unless an external force is applied on it.

Solution 7S.

Solution 8S.

The property of an object by virtue of which it neither changes its state nor tends to change the state is called inertia.

Solution 9S.

Force is that external cause which can move a stationary object or which can stop a moving object.

Solution 10S.

Inertia of a body depends on its mass. Inertia is directly proportional to mass, i.e. greater the mass of a body, greater is its inertia.

Solution 11S.

Examples to show that greater the mass, greater is the inertia of the body are as shown below:

1. If you want to start a car by pushing it, you find that it takes a very large force to overcome its inertia. On the other hand, only a small force is needed to start a child’s express wagon. The difference between the car and express wagon is the difference in mass. The car has a large mass, whereas the wagon has a small one.
2. A cricket ball is more massive than a tennis ball. The cricket ball acquires a much smaller velocity than a tennis ball when the two balls are pushed with equal force for the same time.

Solution 12S.

It is difficult, i.e. a larger force is required to set a loaded trolley (which has more mass) in motion than an unloaded trolley (which has less mass).

Solution 13S.

Two kinds of inertia are as listed below:

1. Inertia of rest.
2. Inertia of motion.

Solution 14S.

Examples of inertia of rest: A coin placed on top of a card remains in place when the card is slightly and quickly jerked horizontally.
Example of inertia of motion: A ball thrown vertically upwards by a person in a moving train comes back to his hand.

Solution 15S.

No, the body will not move because the net force acting on it is zero. Hence, it will remain stationary due to inertia of rest.

Solution 16S.

The motion remains unaffected because the net force acting on it is zero.

Solution 17S.

The net force on the airplane is zero or the upward force is equal to the downward force.

Solution 18S.

If a person jumps out of a moving train and tries to stop immediately, he falls due to inertia of motion. This is because his body tends to move forward with the velocity of the train while his feet are stationary.

Solution 19S.

The reason is that when the card is flicked, a momentary force acts on the card, so it moves away. However, the coin kept on it does not share the motion at once and it remains stationary at its place due to the inertia of rest. The coin then falls down into the tumbler due to the pull of gravity.

Solution 20S.

The reason is that when the ball is thrown, the ball is in motion along with the person and train. Due to the inertia of motion, during the time the ball remains in air, the person and ball move ahead by the same distance. This makes the ball fall back into the thrower’s hand.

Solution 21S.

(a) When a train suddenly starts, the passengers tend to fall backwards. This is because the lower part of the body, which is in contact with the train, begins to move while the upper part of the body tends to maintain its position of rest. As a result, the upper part tends to fall backwards.

(b) The frame of the sliding door being in contact with the floor of the train also comes in motion on start of the train, but the sliding door remains in its position due to inertia. Thus, the frame moves ahead with the train, while the door slides opposite to the direction of motion of the train. Thus, the door may shut or open accordingly.

(c) When the branches of the tree are shaken, they come in motion, while the fruits due to inertia remain in a state of rest. Thus, the larger and weakly attached fruits get detached from the branches and fall down due to the pull of gravity.

(d) When people alight from a moving bus, they continue to run alongside the bus to avoid falling. If they were to stop at once, the feet would come to rest suddenly but the upper part of the body would still be in motion and they would tend to fall forward.

(e) The part of the carpet where the stick strikes comes in motion at once, while the dust particles settled on it remain in the state of rest due to inertia of rest. Thus, a part of the carpet moves ahead with the stick leaving behind the dust particles that fall down due to gravity.

(f) When running, the athlete brings his body in the state of motion. When the body is in motion, it becomes easier to take a long jump.

Solution 1M.

A truck

Solution 2M.

Less force is required for the tennis ball than for the cricket ball.

Solution 3M.

Change the state of motion or state of rest of the body.

Exercise 3(C)

Solution 1S.

Force needed to stop a moving body in a given time depends on its mass and velocity.

Solution 2S.

Linear momentum of a body is the product of its mass and velocity.
Its SI unit is kgms^-1.

Solution 3S.

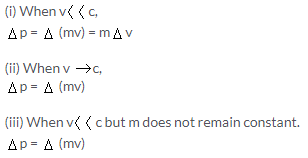
Solution 4S.

Let a force ‘F’ be applied on a body of mass m for a time ‘t’ due to which its velocity changes from u to v. Then,
Initial momentum of body = mu
Final momentum of body = mv
Change in momentum of the body in ‘t’ seconds = mv – mu = m (v – u)
Rate of change of momentum = Change in momentum/time
= [m (v – u)]/t
However, acceleration a = Change in velocity/time = (v – u)/t
Therefore, rate of change of momentum = ma = mass × acceleration
This relation holds true when the mass of the body remains constant.

Solution 5S.

(i) Mass is the measure of inertia.
Let ‘m’ be the mass of the two bodies.
Inertia of body A:Inertia of body B :: m:m
Or, Inertia of body A:Inertia of body B :: 1:1

(ii) Momentum of body A = m (v)
Momentum of body B = m (2v) = 2mv
Momentum of body A:Momentum of body B :: mv:2mv
Or, Momentum of body A:Momentum of body B :: 1:2.

Solution 6S.

(i) Inertia of body A:Inertia of body B :: m:2m
Or, Inertia of body A:Inertia of body B :: 1:2.

(ii) Momentum of body A = m ( 2v) = 2mv
Momentum of body B = (2m) v = 2mv
Momentum of body A:Momentum of body B :: 2 mv:2mv
Or, Momentum of body A:Momentum of body B :: 1:1.

(iii) According to Newton’s 2nd law of motion, rate of change of momentum is directly proportional to the force applied on it. Therefore,
Force needed to stop A:Force needed to stop B :: 1:1.

Solution 7S.

According to Newton’s second law of motion, the rate of change of momentum is directly proportional to the force applied on it and the change of momentum takes place in the direction in which the force is applied.
It gives the quantitative value of force, i.e. it relates the force to the measurable quantities such as acceleration and mass.

Solution 8S.

Newton’s first law of motion gives the qualitative definition of force. It explains the force as the cause of acceleration only qualitatively but Newton’s second law of motion gives the quantitative value of force. It states force as the product of mass and acceleration. Thus, it relates force to the measurable quantities such as acceleration and mass.

Solution 9S.

Mathematical expression of Newton’s second law of motion is as shown below:
Force = Mass x Acceleration

Above relation holds for the following conditions:
(i) When the velocity of the body is much smaller than the velocity of light.
(ii) When the mass remains constant.

Solution 10S.

According to Newton’s second law of motion, the rate of change of momentum is directly proportional to the force applied on it, and the change of momentum takes place in the direction in which the force is applied.

The relation F=ma holds for the following conditions:
(i) When the velocity of the body is much smaller than the velocity of light.
(ii) When the mass remains constant.

Solution 11S.

From Newton’s second law of motion, F = ma.
If F = 0, then a = 0.

This means that if no force is applied on the body, its acceleration will be zero. If the body is at rest, then it will remain in the state of rest and if it is moving, then it will remain moving in the same direction with the same speed. Thus, a body not acted upon by an external force, does not change its state of rest or motion. This is the statement of Newton’s first law of motion.

Solution 12S.

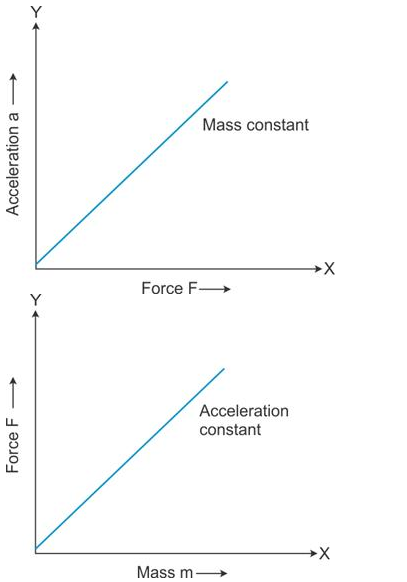
Solution 13S.

If a given force is applied on bodies of different masses, then the acceleration produced in them is inversely proportional to their masses.
A graph plotted for acceleration (a) against mass (m) is a hyperbola.

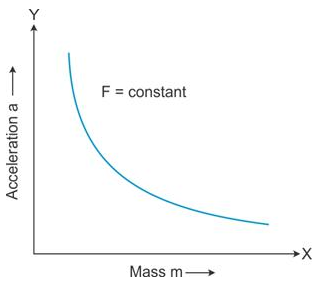
Solution 14S.

The S.I. unit of force is newton.
One newton is the force which acts on a body of mass 1kg and produces an acceleration of 1 m/s², i.e. 1 N = 1 kg × 1 m/s².

Solution 15S.

The C.G.S. unit of force is dyne.
One dyne is the force which acts on a body of mass 1 gramme and produces an acceleration of 1 cms^-2, i.e. 1 dyne = 1 g × 1 cms^-2.

Solution 16S.

The S.I. unit of force is newton and the C.G.S. unit of force is dyne.
1 N = 10⁵ dyne.

Solution 17S.

When a glass vessel falls from a height on a hard floor, it comes to rest almost instantaneously, i.e. in a very short time, so the floor exerts a large force on the vessel and it breaks. However, if it falls on a carpet, then the time duration, in which the vessel comes to rest, increases, so the carpet exerts less force on the vessel and it does not break.

Solution 18S.

(a) We pull our hands back while catching a fast moving cricket ball, because by doing so, we increase the time of catch, i.e. increase the time to bring about a given change in momentum, and hence, the rate of change of momentum decreases. Thus, a small force is exerted on our hands by the ball.

(b) When an athlete lands from a height on a hard floor, his feet comes to rest instantaneously, so a very large force is exerted by the floor on his feet, but if he lands on sand, his feet push the sand for some distance; therefore, the time duration in which his feet comes to rest increases. As a result, the force exerted on his feet decreases and he is saved from getting hurt.

Solution 1M.

Mv

Solution 2M.

N s

Solution 3M.

Solution 4M.

Mass of the body

Solution 1N.

Mass of the body, m = 5kg
Velocity, v = 2 m/s
Linear momentum = mv = (5)(2) kg m/s
= 10 kg m/s

Solution 2N.

Linear momentum = 0.5 kg m/s
Mass, m = 50 g = 0.05 kg
Velocity = Linear momentum/mass
= 0.5/0.05 m/s
= 10 m/s

Solution 3N.

Force, F = 15 N
Mass, m = 2kg
Acceleration, a = F/m [ From Newton’s second law]
Or, a = (15/2) ms^-2
Or, a = 7.5 ms^-2

Solution 4N.

Force, F = 10 N
Mass, m = 5kg
Acceleration, a = F/m [ From Newton’s second law]
Or, a = (10/5) ms^-2
Or, a = 2 ms^-2

Solution 5N.

Mass, m = 0.5 kg.
Acceleration, a = 5 ms^-2
Force, F = ma   [ From Newton’s second law]
Or, F = (0.5) (5) N = 2.5 N.

Solution 6N.

Force, F = 10 N
Mass, m = 2 kg
Time, t = 3 s
Initial velocity, u = 0 m/s.

(i) Let v be the final velocity acquired.
From Newton’s second law,
F = ma.
Or, a = F/m = 10/2 = 5 ms^-2.

From the 1^st equation of motion,
a = (v – u)/t
Or, v = at + u.
Or, v = (5)(3) + 0 = 15 m/s.

(ii) Change in momentum = Final momentum – initial momentum
Δp = mv – mu.
Or, Δp = m (v – u).
Or, Δp = 2 ( 15 – 0) = 30 kg m/s.

Solution 7N.

Mass, m = 100 kg
Distance moved, s = 100 m
Initial velocity, u = 0

(i) Because the body moves through a distance of 100 m in 5 s,
Velocity of the body = Distance moved / time taken
Velocity = (100/5) = 20 m/s

(ii) From Newton’s third equation of motion,
v²  u² = 2as.
Or, a = (v²  u²) /2s.
Or, a = [ (20²  0²)/ 2(100) ] ms^-2.
Or, a = 2 ms^-2.

(iii) Force, F = ma
Or, F = (100) (2) N.
Or, F = 200 N.

Solution 8N.

Slope of a velocity-time graph gives the value of acceleration.
Here, slope = 20/5 = 4 m/s².
Or, acceleration, a = 4 m/s².
Force = Mass × Acceleration.
Given mass, m = 100 g = 0.1 kg.
Force = (0.1) (4) = 0.4 N.

Solution 9N.

Mass, m = 2 kg
Initial velocity, u = 0
Final velocity, v = 2 m/s
Time, t = 0.1 s
Acceleration = Change in velocity/time
Or, a = (v – u) /t
Or, a = (2 – 0)/ 0.1 = 20 ms^-2.
Force = Mass x Acceleration
Or, F = (2) (20) = 40 N.

Solution 10N.

Mass, m = 100g = 0.1 kg.
Initial velocity, u = 30 m/s.
Final velocity, v = 0.
Time, t = 0.03 s.
Acceleration = Change in velocity/time.
Or, a = (v – u)/t.
Or, a = (0 – 30)/ 0.03 = -1000 ms^-2.
Here, negative sign indicates retardation.
Now, Force = Mass x Acceleration
Or, F = (0.1) (1000) = 100 N.

Solution 11N.

Mass, m = 480 kg.
Initial velocity, u = 54 km/hr = 15 m/s.
Final velocity, v = 0.
Time, t = 10 s.
Acceleration = Change in velocity/time.
Or, a = (v – u)/t.
Or, a = (0 – 15)/10 = -1.5 ms^-2.
Here, negative sign indicates retardation.
Now, Force = Mass x Acceleration
Or, F = (480) (1.5) = 720 N.

Solution 12N.

Mass, m = 50 gm = 0.05 kg.
Initial velocity, u = 100 m/s.
Final velocity, v = 0.
Distance, s = 2cm = 0.02 m.

(i) Initial momentum = mu = (0.05) (100) = 5 kg m/s.
(ii) Final momentum = mv = (0.05) (0) = 0 kg m/s.

(iii) Acceleration, a = (v² – u²)/2s.
Or, a = (0² – 100²)/ 2(0.02).
Or, a = – 2.5 x 10⁵ ms^-2.
Therefore, retardation is 2.5 x 10⁵ ms^-2.

(iv) Force, F = ma
Or, F = (0.05 kg) (2.5 x 10⁵ ms^-2)
Or, F = 12500 N

Solution 13N.

Let the force be F.
Force F causes an acceleration, a = 10 m/s² in a body of mass, m = 500 g or 0.5 kg
Thus, F = ma
Or, F = (0.5) (10) = 5 N
Let a’ be the acceleration which force F (=5N) cause on a body of mass, m’ = 5 kg.
Then, a’ = F/m’.
Or, a’ = (5/5) ms^-2.
Or, a’ = 1 ms^-2.

Solution 14N.

Initial velocity, u = 30 m/s
Final velocity, v = 0
Time, t = 2s
Force, F = 1500 N

Here, a = (v – u)/t = (0 – 30)/ 2 = – 15 ms^-2. Here, negative sign indicates retardation.
Now, F = ma.
Or, m = F/a = (1500/ 15) = 100 kg.

(a) Change in momentum = Final momentum – Initial momentum
Or, Δp = m (v – u)
Or, Δp = 100 (0 – 30)
Or, Δp = 3000 kg m/s

(b) Acceleration, a = (v – u)/t.
Or, a = (0 – 30)/ 2 = – 15 ms^-2,
Here, negative sign indicates retardation.
Thus, retardation = 15 ms^-2.

(c) From Newton’s second law of motion,
F = ma
Or, m = F/a = (1500/ 15) = 100 kg.

Exercise 3(D)

Solution 1S.

Newton’s third law explains how a force acts on an object.

Solution 2S.

According to Newton’s third law of motion, to every action there is always an equal and opposite reaction. The action and reaction act simultaneously on two different bodies.

Solution 3S.

Law of action and reaction: In an interaction of two bodies A and B, the magnitude of action, i.e. the force F_AB applied by the body B on the body A, is equal in magnitude to the reaction, i.e., the force F_BA applied by the body A on the body B, but they are in directions opposite to each other.

Examples:

1. When a book is placed on a table, it does not move downwards. It implies that the resultant force on the book is zero, which is possible only if the table exerts an upward force of reaction on the book, equal to the weight of the book.
2. While moving on the ground, we exert a force by our feet to push the ground backwards; the ground exerts a force of the same magnitude on our feet forward, which makes it easier for us to move.

Explanation: In the above stated example, there are two objects and two forces. In the first example, the weight of the book acts downwards (action) and the force of the table acts upwards (reaction).
In the second example, our feet exerts a force on the ground (action) and the ground exerts an equal and opposite force (reaction) on our feet.

Solution 4S.

(a) Action: Force exerted on the bullet.
Reaction: Recoil experienced by the gun.

(b) Action: The force exerted by the hammer on the nail.
Reaction: The force applied by the nail on the hammer.

(c) Action: Weight of the book acting downwards.
Reaction: Force acted by the table upwards.

(d) Action: Force exerted by the rocket on the gases backwards.
Reaction: Force exerted by outgoing gases on the rocket in forward direction.
(e) Action: Force exerted by the feet on the ground in backward direction.
Reaction: Force exerted by the ground on feet in forward direction.

(f) Action: Force exerted by a moving train on a stationary train.
Reaction: Force exerted by a stationary train on a moving train.

Solution 5S.

When a rocket moves in space, it pushes gases outside, i.e. the rocket applies force on the gases in the backward direction. As a reaction, the gases put equal amount of force on the rocket in the opposite direction and the rocket moves in the forward direction.

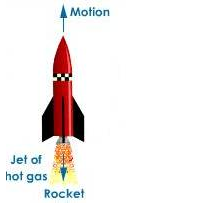
Solution 6S.

When a man fires a bullet from a gun, a force F is exerted on the bullet (action), and the gun experiences an equal and opposite recoil (reaction) and hence gets recoiled.

Solution 7S.

When a man exerts a force (action) on the boat by stepping into it, its force of reaction makes him step out of the boat, and the boat tends to leave the shore due to the force exerted by the man (i.e. action).

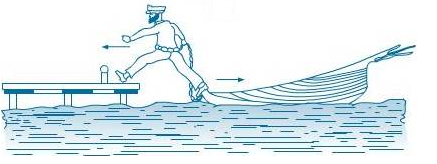
Solution 8S.

Couple two spring balances A and B as shown in the figure. When we pull the balance B, both the balances show the same reading indicating that both the action and reaction forces are equal and opposite. In this case, the pull of either of the two spring balances can be regarded as action and that of the other balance as the reaction.

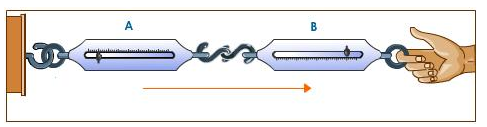
Solution 9S.

To move a boat, the boatman pushes (action) the water backwards with his oar. In this response, the water exerts an equal and opposite force (reaction) in the forward direction on the boat due to which the boat moves ahead.

Solution 10S.

A person pushing a wall hard (action) by his palm, experiences a force (reaction) exerted by the wall on his palm in the opposite direction; thus, he is liable to fall backwards.

Solution 11S.

Yes, action and reaction act simultaneously.

Solution 12S.

Yes, action and reaction are equal in magnitude.

Solution 13S.

When a falling ball strikes the ground, it exerts a force on the ground. The ground exerts a force back at the ball in the opposite direction. This is the reason the ball rises upwards.

Solution 14S.

The given statement is wrong.
Reason: According to Newton’s third law of motion, the action and reaction act simultaneously on different bodies. Hence they do not cancel each other.

Solution 1M.

Explains the way the force acts on a body.

Solution 2M.

Different bodies in opposite directions

Solution 1N.

The wall exerts an equal force of 10 N on the boy in the opposite direction, i.e. west.

Solution 2N.

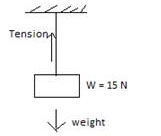
(a) A block exerts 15 N force (weight) on the string downwards.
(b) The string exerts an equal force of 15 N on the block in the opposite direction, i.e. upward direction (tension).

Exercise 3(E)

Solution 1S.

Newton’s law of gravitation: Every particle in the universe attracts every other particle with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them, and the direction of the force is along the line joining the masses.

Solution 2S.

Gravitational force is always attractive.

Solution 3S.

Here G is a constant of proportionality called the universal gravitational constant.

Solution 4S.

The gravitational force of attraction between two masses is inversely proportional to the square of distance between them.

Solution 5S.

If the distance between the masses becomes half, the force reduces to one-fourth.

Solution 6S.

The gravitational constant is defined as the force of attraction between two bodies of unit mass separated by a unit distance.

Solution 7S.

The value of G in the S.I. system is 6.67 x 10^-11Nm²kg^-2.

Solution 8S.

The gravitational force of attraction is significant to explain the motion of heavenly bodies, e.g. motion of planets around the Sun, motion of the Moon around the Earth etc.

Solution 9S.

The force with which the Earth attracts a body towards its centre is called the force due to gravity.

Solution 10S.

The force due to gravity on a body of mass m kept on the surface of Earth (mass=M and radius=R) is equal to the force of attraction between the Earth and that body.

Solution 11S.

The rate at which the velocity of a freely falling body increases is called acceleration due to gravity. Its S.I. unit is m/s².

Solution 12S.

The average value of ‘g’ on the Earth’s surface is 9.8 m/s².

Solution 13S.

Let g be the acceleration due to gravity on the Earth’s surface (mass = M and radius = R).

Solution 14S.

Acceleration due to gravity (g) is directly proportional to universal gravitational constant (G).

Solution 15S.

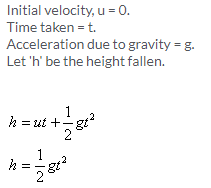
Solution 16S.

If a body is thrown vertically up with an initial velocity u to a height h, then there will be retardation (a = – g).
At the highest point, the final velocity v = 0.
Thus, from the third equation,

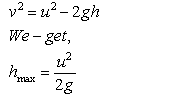
Solution 17S.

Mass: The mass of a body is the quantity of matter it contains.
Weight: The weight of a body is the force with which the Earth attracts it.

Solution 18S.

Mass is a scalar quantity, but weight is a vector quantity. Mass is the measure of the quantity of matter contained in a body, but weight is the measure of force with which the Earth attracts the body. Mass of a body is always constant but weight varies from place to place.

Solution 19S.

The S.I. unit of mass is kg and that of weight is newton.

Solution 20S.

W = mg
At the centre of Earth, g = 0.
Therefore, W = 0.

Solution 21S.

Mass of a body is always constant.

Solution 22S.

1 kgf = 9.8 N.
One kilogramme force is the force due to gravity on a mass of 1 kilogramme.

Solution 1M.

Always attractive

Solution 2M.

6.7 x 10^-11 N m² kg^-2

Solution 3M.

6.7 x 10^-11 N

Solution 4M.

METHOD: Let’t’ be the time in which the body reaches its maximum height.
Initial velocity = u.
Final velocity (at the highest point) = 0.
Acceleration due to gravity = g (negative sign indicates the body is moving against gravity).
Using the first equation of motion,
v = u + gt.
We get,
0 = u gt
Or t = u/g
Now total time for which the ball remains in air = Time of ascent + Time of descent
Because time of ascent = Time of descent,
Total time taken = u/g + u/g = 2u/g

Solution 5M.

19.6 m s^-1

METHOD: Given, u = 0
g = 9.8 m/s²
Time t = 2s
Let ‘v’ be the velocity of object on reaching the ground.
Using the first equation of motion,
v = u + gt
We get,
v = 0 + (9.8) (2)
Or, v = 19.6 m/s.

Solution 1N.

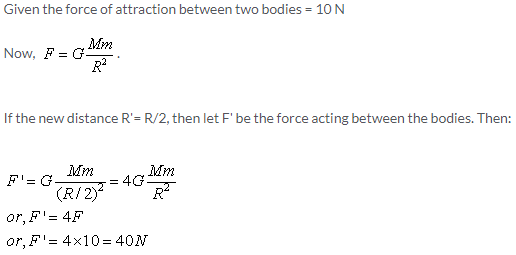
Solution 2N.

Weight = mg
W = (5) (9.8) = 50 N.
Assumption: Value of acceleration due to gravity = 9.8 m/s².

Solution 3N.

Mass = 10 kg
(i) Weight (in kgf) = 10 x 1 kgf = 10 kgf
[1 kgf = 9.8 N]
(ii) Weight (in newton) = 10 x 9.8 = 98 N.

Solution 4N.

Mass = 5 kg.
g = 9.8 m/s2.
Let F be the force of gravity,
F = mg.
F = (5) (9.8) = 49 N.
Force of gravity always acts downwards.

Solution 5N.

Weight, W = 2.0 N
g = 9.8 m/s²
Let ‘m’ be the mass of the body.
W = mg
Or, m = W/g = (2/9.8) kg = 0.2 kg.

Solution 6N.

Weight of the body on Earth = 98 N.
Acceleration due to gravity on Earth = 9.8 m/s².
Let ‘m’ be the mass of the body on Earth.
m = W/g
m = (98/9.8) = 10 kg
Thus, the mass of the body is 10 kg, which always remains constant.
(a) Mass on moon = mass on Earth = 10 kg
(b) Let weight on moon is W’.
W’ = mass x acceleration due to gravity on the Moon.
[Given, acceleration due to gravity on the Moon = 1.6 m/s²]
W’ = 10 x 1.6 =16 N.

Solution 7N.

Man’s weight on Earth = 600 N
Man’s weight on the Moon = (1/6) man’s weight on Earth;
Because the acceleration due to gravity on the Moon is 1/6th that of Earth and w = mg.
Therefore, man’s weight on Moon = (600/6) = 100 N.

Solution 8N.

Mass, m = 10.5 kg
G = 10 m/s²
(a) Force, F = mg
F = (10.5) (10) = 105 N
(b) Weight, w = mg
w = (10.5) (10) = 105 N

Solution 9N.

Let ‘S’ be the height.
Time taken, t = 3s; g = 9.8 m/s²
Initial velocity, u = 0 (because the body starts from rest)

(a) Using the second equation of motion,
S = ut + (1/2) gt²
We get,
S = 0 + (1/2) (9.8) (3) (3)
S = 44.1 m

(b) Let ‘v’ be the velocity with which the ball strikes the ground.
Using the third equation of motion,
v² – u² = 2gs
or, v² – 0² = 2(9.8) (44.1)
or, v² = 864.36
or, v = 29.4 m/s

Solution 10N.

Mass, m = 5kg
Force, F = mg
F = (5) (9.8) = 49 N
Assumption: Value of acceleration due to gravity is 9.8 m/s².

Solution 11N.

Given, maximum height reached, s = 20 m
Acceleration due to gravity, g = 10 m/s²

(a) Let ‘u’ be the initial velocity.
At the highest point, velocity = 0
Using the third equation of motion,
v²   u² = 2gs
or, 0  u² = 2 (10) (20) m/s
or, u² =  (400) m/s [Negative sign indicates that the motion is against gravity]
or, u = 20 m/s

(b) Let v’ be the final velocity of the ball on reaching the ground.
Considering the motion from the highest point to ground,
Velocity at highest point = 0 = Initial velocity for downward journey of the ball.
Distance travelled, s = 20m
Using the third equation of motion,
v²  u² = 2gs
or, v²  0 = 2 (10) (20) m/s
or, v² = 400 m/s
or, v = 420 m/s

(c) Now total time for which the ball remains in air, t = 2u/g.
Or, t = 2 (20)/(10).
Or, t = 4s.

Solution 12N.

Initial velocity u = 0
Final velocity = 20 m/s
g = 10 m/s²
Let ‘h’ be the height of the tower.
Using the third equation of motion,
v² – u² = 2gs
or, (20)² – 0 = 2 (10) h
or, h = 20 m

Solution 13N.

Total time of journey = 6 s
g = 10 m/s²

(i) Let ‘H’ be the greatest height.
Time of ascent, t = 6/2 = 3 s,
For ascent, initial velocity, u = 0
Using the second equation of motion,
H = ut + (1/2) gt²
H = 0 + (1/2) (10) (3) ²
H = 45 m

(ii) Let u’ be the initial velocity.
Final velocity, v = 0
Using the third equation of motion,
v² – u² = 2gH
or, v² – 0 = 2(10) (45)
or, v² = 900
or, v = 30 m/s

Solution 14N.

Initial velocity, u = 20 m/s
Time, t = 2s
g = 10 m/s²
Maximum height reached in 2s, H = (1/2) gt²
Or, H = (1/2) (10) (2) ²
Or, H = 20 m

Solution 15N.

(a) Height, s = 80m
g = 10 m/s²
Using the second equation of motion,
S = ut + (1/2) gt²
Or, 80 = 0+ (1/2) (10) (t) ²
Or, (t) ² = 16
Or, t = 4s

(b) Let ‘v’ be the velocity on reaching the ground.
Using the third equation of motion,
v² – u² = 2gH
or, v² – 0 = 2(10) (80)
or, v² = 1600
or, v = 40 m/s

Solution 16N.

Given time t = 2.5, g = 9.8 m/s²
Height, H = (1/2) gt²
Or, H = (1/2) (9.8) (2.5)²
Or, H = 30.6 m

Solution 17N.

Initial velocity, u = 49 m/s
g = 9.8 m/s²

(i) Let H be the maximum height attained.
At the highest point, velocity = 0.
Using the third equation of motion,
v² – u² = 2gH
or, 0 – 49² = 2(-9.8) (H)
or, H = (49²)/ 19.6
or, H = 122.5 m

(ii) Total time of flight is given by t = 2u/g
Or, t = 2(49)/ 9.8
Or, t = 10 s

Solution 18N.

Initial velocity u = 0
Time t = 4 s
g = 10 m/s²
Let ‘H’ be the height of the tower.
Using the second equation of motion,
H = ut + (1/2) gt²
Or, H = 0 + (1/2)(10)(4)²
Or, H = 80 m

Solution 19N.

(i) Time t =20 s
g = 10 m/s²
Let ‘D’ be the depth of the well.
Using the second equation of motion,
D = ut + (1/2) gt²
D = 0 + (1/2)(10)(20) ²
D = 2000 m

(ii) Speed of sound = 330 m/s
Depth of well = 2000 m
Time taken to hear the echo after the pebble reaches the water surface = Depth/speed
= (2000/330) s
= 6.1 s
Time taken for pebble to reach the water surface = 20 s.
Therefore, the total time taken to hear the echo after the pebble is dropped = 20 + 6.1 = 21.6 s.

Solution 20N.

Let x be the height of the tower.
Let h be the distance from the top of the tower to the highest point as shown in the diagram.

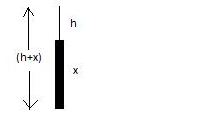
Initial velocity u = 19.6 m/s
g = 9.8 m/s²
At the highest point, velocity = 0
Using the third equation of motion,
v² – u² = 2gh
Or, – (19.6) ² = 2 (-9.8) h
Or, h = 19.6 m
If the ball takes time t₁ to go to the highest point from the top of building, then for the upward journey from the relation, v = u – gt,
0 = 19.6 – (9.8) (t₁)
Or, t₁ = 2s

(ii) Let us consider the motion for the part (x+h)
Time taken to travel from highest point to the ground = (5 – 2) = 3s
Using the equation s = ut + (1/2) gt²
We get,
(x + h) = 0 + (1/2) (9.8) (3) ²
Or, (x + 19.6) = 44.1 m
Or, x = 44.1 – 19.6 = 24.5 m
Thus, height of the tower = 24.5 m

(iii) Let v be the velocity of the ball on reaching the ground.
Using the relation, v = u + gt
We get:
v = 0 + (9.8) (3)
Or, v = 29.4 m/s

More Resources for Selina Concise Class 9 ICSE Solutions

• Concise Physics Class 9 ICSE Answers
• Concise Chemistry Class 9 ICSE Answers
• Concise Biology Class 9 ICSE Answers
• ICSE Class 9 Maths Selina Solutions