Selina Concise Chemistry Class 9 ICSE Solutions Study of Gas Laws

Selina Concise Chemistry Class 9 ICSE Solutions Study of Gas Laws

ICSE SolutionsSelina ICSE Solutions

APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 9 Chemistry Chapter 8 Atmospheric Pollution. You can download the Selina Concise Chemistry ICSE Solutions for Class 9 with Free PDF download option. Selina Publishers Concise Chemistry for Class 9 ICSE Solutions all questions are solved and explained by expert teachers as per ICSE board guidelines.

Download Formulae Handbook For ICSE Class 9 and 10

Selina ICSE Solutions for Class 9 Chemistry Chapter 7 Study of Gas Laws

Page No: 122

Question 1.
What do you understand by gas?
Solution:
The state of matter in which inter-particle attraction is weak and inter-particle space is so large that the particles become completely free to move randomly in the entire available space, is known as gas.

Question 2.
Give the assumptions of the kinetic molecular theory.
Solution:
The main assumption of the kinetic molecular theory of gases are as follows:

1. All gases are made up of a large number of extremely small particles called molecules.
2. There are large vacant spaces between the molecules of a gas so that actual volume of the molecules of a gas is negligible as compared to the total volume occupied by the gas.
3. The molecules of a gas are always in a state of constant random motion in straight lines in all possible direction.
4. There are negligible attractive forces between the molecules of a gas.
5. There is no effect of gravity on the motion of the molecules of a gas.
6. The average kinetic energy of the molecules of a gas is directly proportional to that of the Kelvin temperature of the gas.
7. The molecules are perfectly elastic so that there is no net loss of energy during molecular collisions.
8. The pressure of a gas is due to the bombardment of the molecules of a gas against the walls of a container.

Question 3.
During the practical session in the lab when hydrogen sulphide gas having offensive odour is prepared for some test, we can smell the gas even 50 metres away. Explain the phenomenon.
Solution:
In a laboratory, when hydrogen sulphide gas is prepared, it can be smelt even at 50 meters away. This is due to the phenomenon called Diffusion.

Diffusion is a process of intermixing of two substances kept in contact.

The inter-particle or inter molecular spaces in a gas are very large. When hydrogen sulphide gas is produced, its particle collides with air particles. Due to the collisions of particles, they start moving in all possible directions. As a result of which the two gases mix with each other forming a homogeneous mixture of a gas. Thus, the released gas can be smelt to a long distance.

Solution 4.

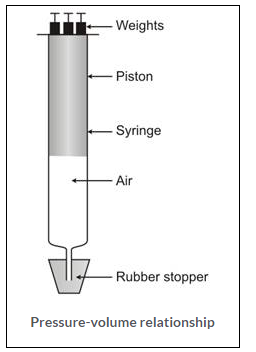
Pressure and volume relationship of gases-
Experiment: Take a 10 ml syringe fitted with a piston. Raise the latter to the 10 ml mark and wrap an adhesive tape over its nozzle. Fit the wrapped nozzle tightly into a hole, bored half way through a rubber stopper.

Observation: On placing some weight on the piston (to put pressure), the piston moves downward and reduces the volume of air. Gradually, put more weight. The piston moves further downward and the volume of the air is further reduced.

Now remove the weights one by one. You will notice that, on decreasing the pressure, the piston moves upward as such the volume of the air increases.

Conclusion:

1. An increase in pressure at constant temperature causes a decrease in the volume of a gas; conversely, if the volume of a fixed mass of a gas at constant temperature is decreased, the pressure of the gas increases.
2. A decrease in pressure at constant temperature causes a increase in the volume of a gas; conversely, if the volume of a fixed mass of a gas at constant temperature is increased, the pressure of the gas decreases.

Solution 5.

The molecular motion is directly proportional to the temperature.
As temperature increases, molecular motion increases because the molecule possesses certain kinetic energy. And as the temperature decreases, molecular motion also decreases. Thus, when temperature is zero, molecular motion stops or ceases.

Question 6.
State (i) the three variables for gas laws and (ii) SI units of these variables.
Solution:
The three variables for gas laws are:

1. Volume, V
2. Pressure, P
3. Temperature, T

These three are called as the Standard variables. S.I. unit of volume is cubic meter (m³).
S.I. unit of pressure is Pascal (Pa).
S.I. unit of temperature is Kelvin (K) or degree Celsius (⁰C).

Question 7.
State Boyle’s Law.
Give its
i. Mathematical expression
ii. Graphical representation and
iii. Significance
Solution:
Boyle’s law: At constant temperature, the volume of a definite mass of any gas is inversely proportional to the pressure of the gas.                       Or
Temperature remaining constant, the product of the volume and pressure of the given mass of a dry gas is constant.

Mathematical representation:

According to Boyle’s Law,

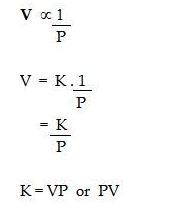
Where K is the constant of proportionality if V’ and P’ are some other volume and pressure of the gas at the same temperature then,

temperature, a straight line passing through the origin is obtained.

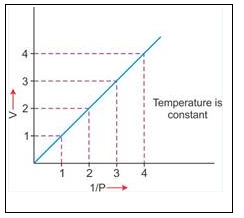
2. V vs P : Variation in volume (V) plotted against pressure (P) at a constant temperature, a hyperbolic curve in the first quadrant is obtained.

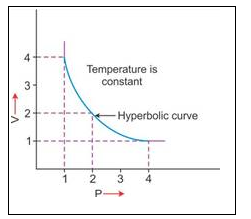
3. PV vs P : Variation in PV plotted against pressure (P) at a constant temperature, a straight line parallel to X-axis is obtained.

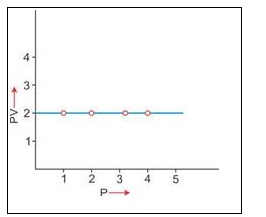
Significance of Boyles law:

According to Boyles law, on increasing pressure, volume decreases. The gas becomes denser. Thus, at constant temperature, the density of a gas is directly proportional to the pressure.

At higher altitude, atmospheric pressure is low so air is less dense. As a result, lesser oxygen is available for breathing. This is the reason that the mountaineers have to carry oxygen cylinders with them.

Question 8.
Explanation of Boyle’s Law on the basis of kinetic theory of matter.
Solution:
According to kinetic theory of matter, the number of particles present in a given mass and the average kinetic energy is constant.

If the volume of given mass of a gas is reduced to half of its original volume. The same number of particles will have half space to move.

As a result, the number of molecules striking the unit area of the walls of the container at given time will get doubled of the pressure will also get doubled.

Alternatively, if the volume of a given mass of a gas is doubled at constant temperature, same number of molecules will have double space to move. Thus, number of molecule striking the unit area of the walls of container at a given time will become one half of original value. Thus, pressure will also get reduced to half of original pressure. Hence, it is seen that if pressure increases, volume of a gas decreases at constant temperature and this is Boyle’s law.

Question 9.
The molecular theory states that the pressure exerted by a gas in a closed vessel results from the gas molecules striking against the walls of the vessel. How will the pressure change if
The temperature is doubled keeping the volume constant
The volume is made half of its original value keeping the T constant
Solution:
(a) Pressure will be doubled.
(b) Pressure remains the same.

Question 10.
a. State Charles’s law.
b. Give its
i. Graphical representation
ii. Mathematical expression and
iii. Significance
Solution:

Charless Law

At constant pressure, the volume of a given mass of a dry gas increases or decreases by 1/273 of its original volume at 00C for each degree centigrade rise or fall in temperature.

For Temperature = Conversion from Celsius to Kelvin
1 K = ⁰C + 273
For example,
20^oC = 20 + 273 = 293 K

Graphical representation of Charles law

T vs V: The relationship between the volume and the temperature of a gas can be plotted on a graph, A straight line is obtained.

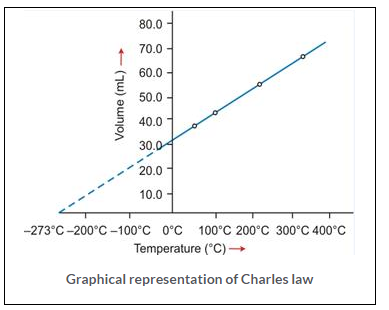
Significance of Charles’ Law: Since the volume of a given mass of gas is directly proportional to its temperature, hence the density decreases with temperature. This is the reason that:

(a) Hot air is filled in the balloons used for meteorological purposes. (b) Cable wires contract in winters and expand in summers.

Question 11.
Explanation Of Charles’ Law on the basis of kinetic theory of matter is as follows:
Solution:
According to kinetic theory of matter, the average kinetic energy of the gas molecules is directly proportional to the absolute temperature. Thus, when the temperature of a gas is increased, the molecules would move faster and the molecules will strike the unit area of the walls of the container more frequently and vigorously. If the pressure is kept constant, the volume increases proportionately. Hence, at constant pressure, the volume of a given mass of a gas is directly proportional to the temperature (Charles’ law).

Question 12.
Define absolute zero and absolute scale of temperature. Write the relationship between °C and K.
Solution:
Absolute zero

Absolute or Kelvin scale of temperature

The temperature scale with its zero at – 273^oC and each degree equal to one degree on the Celsius scale is called Kelvin or the absolute scale of temperature.

Conversion of temperature from Celsius scale to Kelvin scale and vice versa

The value on the Celsius scale can be converted into Kelvin scale by adding 273 to it.
For example,
20^oC = 20 + 273 = 293 K

Question 13.
(a) What is the need for the Kelvin scale of temperature?
(b) What is the boiling point of water on the Kelvin scale? Convert it into centigrade scale.
Solution:
(a) The behaviour of gases shows that it is not possible to have temperature below 273.15C. This act has led to the formulation of another scale known as Kelvin scale. The real advantage of the Kelvin scale is that it makes the application and the use of gas laws simple. Even more significantly, all values on the Kelvin scale are positive.

(b) The boiling point of water on the Kelvin scale is 373 K.
Now, K = C + 273 and C = K – 273
Kelvin scale can be converted to degree Celsius by subtracting 273 from it. So, boiling point of water on centigrade sale is : 373 K – 273 = 100C

Question 14.
(a) Define STP or NTP.
(b) Why is it necessary to compare gases at STP?
Solution:
(a) Standard or Normal Temperature and Pressure (S.T.P. or N.T.P.)

The pressure of the atmosphere which is equal to 76 cm or 760 mm of mercury is referred to as S.T.P. or N.T.P. The full form for S.T.P. is Standard Temperature and Pressure or Normal Standard temperature and pressure denotes 0^oC or 273K.

Value: The standard values chosen are 0^oC or 273 K for temperature and 1 atmospheric unit (atm) or 760 mm of mercury for pressure.
The standard values chosen are 0^oC or 273 K for temperature and 1 atmospheric unit (atm) or 760 mm of mercury for pressure.
Standard temperature = 0^oC = 273 K
Standard pressure = 760 mm Hg
= 76 cm of Hg
= 1 atmospheric pressure (atm)

(b) Because the volume of a given mass of dry enclosed gas depends upon the pressure of the gas and temperature of the gas in Kelvin so to express the volume of the gases we compare these to S.T.P.

Solution 15.

(a) (i) C = ^oC (ii) K = 273K
(b) (i) 1 atm (ii) 760 mm Hg (iii) 76 cm Hg. (iv) 1, torr = 133.32 Pascal

Question 16.
What is the relationship between the Celsius and Kelvin scales of temperature?
Convert (i) 273°C to Kelvin and (ii) 293 K to °C.
Solution:
Temperature on Kelvin scale (K) = 273 + Temperature on Celsius scale
Or K = 273 + ^oC

(i) 273C in Kelvin
t ^oC = t K – 273
273^oC = t K – 273
T K = 273 + 273 = 546 K
273^oC = 546 K

(ii) 293 K in ^oC
t ^oC = 293 – 273
t ^oC = 20^oC
293 K = 20^oC

Question 17.
State the laws which are represented by the following graphs.

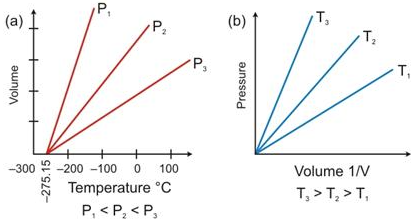
Solution:

(a) Charles’s Law
(b) Boyles Law

Question 18.
Give reasons for the following:
(a) All temperature in the absolute (Kelvin) scale are in positive figures.
(b) Gases have lower density compared to solids or liquids.
(c) Gases exert pressure in all directions.
(d) It is necessary to specify the pressure and temperature of a gas while stating its volume.
(f) Inflating a balloon seems to violate Boyle’s law.
(g) Mountaineers carry oxygen cylinders with them.
(h) Gas fills the vessel completely in which it is kept.
Solution:
(a) The real advantage of the Kelvin scale is that it makes the application and use of gas laws simple. Even more significantly, all values on the scale are positive. Thus, removing the problem of negative (-) values on the Celsius scale.

(b) The mass of a gas per unit volume is very small due to the large intermolecular spaces between the molecules. Therefore, gases have low density. Whereas in solids and liquids, the mass is higher and intermolecular spaces are negligible.

(c) At a given temperature, the number of molecules of a gas striking against the walls of the container per unit time per unit area is the same. Thus, gases exert the same pressure in all directions.

(d) Since the volume of a gas changes remarkably with change in temperature and pressure, it becomes necessary to choose standard value of temperature pressure.

(e) According to Boyle’s Law, the volume of a given mass of a day gas is inversely proportional to its pressure at constant temperature.

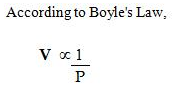
When a balloon is inflated, the pressure inside the balloon decreases and according to Boyle’s Law, the volume of the gas should increase. But this does not happen. On inflation of a balloon along with reduction of pressure of air inside balloon, the volume of air also decreases. And this violates Boyle’s law.

(f) Atmospheric pressure is very low at high altitudes, volume of air increases thus air becomes less dense. Because volume is inversely proportional to density. Hence, lesser volume of oxygen is available for breathing. Thus, mountaineers have to carry oxygen cylinders with them.

(g) In gas as inter-particle attraction is weak and inter-particle space is so large that the particles become completely free to move randomly in the entire available space and takes the shape of the vessel in which it is kept.

Question 19.
How did Charles’s law lead to the concept of absolute scale of temperature?
Solution:
The temperature scale with its zero at -273^oC and where each degree is equal to degree on the Celsius scale is called the absolute scale of temperature.

The temperature -273^oC is called the absolute zero. Theoretically, this is the lowest temperature that can never be reached. At this temperature all molecular motion ceases.

The temperature – 273^oC is called absolute zero.

Question 20.
What is meant by aqueous tension? How is the pressure exerted by a gas corrected to account for aqueous tension?
Solution:
Gases like nitrogen, hydrogen are collected over water as shown in the figure. When the gas is collected over water. The gas is moist and contains water vapour. The total pressure exerted by this moist gas is equal to the sum of the partial pressures of the dry gas and the pressure exerted by water vapour: The partial pressure of water vapour is also known as Aqueous tension.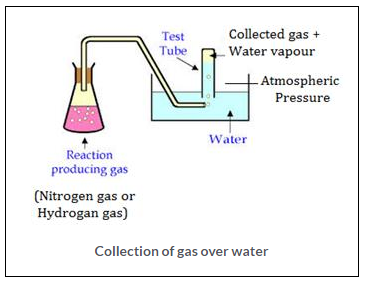
P_total = P_gas + P_{water vapour}
P_gas = P_total – P_{water vapour}
Actual Pressure of gas = Total pressure – Aqueous tension

Question 21.
State the following:

1. Volume of a gas at 0 Kelvin
2. Absolute temperature of a gas at 7°C
3. Gas equation
4. Ice point in absolute temperature
5. STP conditions

Solution:
(a) The volume of gas is zero.
(b) The absolute temperature is 7 + 273 = 280 K
(c) The gas equation is-

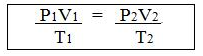
(d) Ice point = 0 + 273 = 273 K
(e) Standard Temperature is taken as 273 K or °C
Standard pressure is taken as 1 atmosphere (atm) or 760 mm Hg.

Question 22.
Choose the correct answer:
a. The graph of PV vs P for a gas is
i. Parabolic
ii. Hyperbolic
iii. A straight line parallel to the X-axis
iv. A straight line passing through the origin
b. The absolute temperature value that corresponds to 27°C is
i. 200 K
ii. 300 K
iii. 400 K
iv. 246 K
c. Volume-temperature relationship is given by
i. Boyle
ii. Gay-Lussac
iii. Dalton
iv. Charles
d. If pressure is doubled for a fixed mass of a gas, its volume will become
i. 4 times
ii. ½ times
iii. 2 times
iv. No change
Solution:
(a) (iii) Straight line paralled to X- axis.
(b) (ii) 27C = 27 + 273 = 300 K
(c) (iv) Charles
(d) (ii) 1/2 times

Question 23.
Match the following:

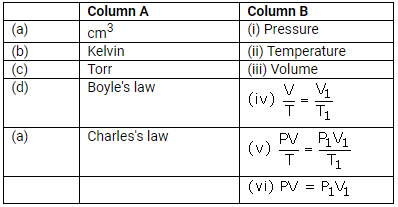
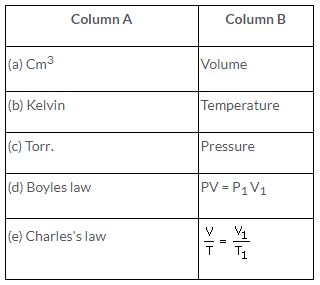
Solution:

Question 24.
Correct the following statements:
Volume of a gas is inversely proportional to its pressure at constant temperature.
Volume of a fixed mass of a gas is directly proportional to its temperature, pressure remaining constant.
0°C is equal to zero Kelvin.
Standard temperature is 25°C.
Boiling point of water is 273 K
Solution:
(a) Volume of a gas is directly proportional to the pressure at constant temperature.
(b) Volume of a fixed mass of a gas is inversely proportional to the temperature, the pressure remaining constant.
(c) -273C is equal to zero Kelvin.
(d) Standard temperature is 0°C
(e) The boiling point of water is -373 K.

Question 25
The average kinetic energy of the molecules of a gas is proportional to the ………….
The temperature on the Kelvin scale at which molecular motion completely ceases is called……………
If temperature is reduced to half, ………….. would also reduce to half.
The melting point of ice is …………. Kelvin
Solution:
(a) Absolute temperature
(b) Absolute zero
(c) Volume
(d) 273

Page No: 123 Numericals

Question Num 1
What will be the minimum pressure required to compress 500 dm³ of air at 1 bar to 200 dm³ temperature remaining constant.
Solution:

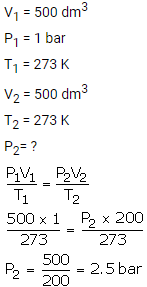
Question Num 2.
2 litres of a gas is enclosed in a vessel at a pressure of 760 mmHg. If temperature remains constant, calculate pressure when volume changes to 4 dm³.
Solution:

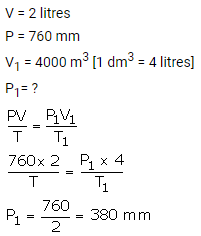
Question Num 3.
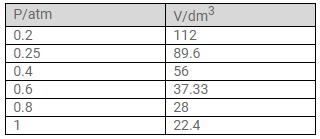
At constant temperature, the effect of change of pressure on volume of a gas was as given below:

Plot the following graphs
1. P vs V
2. P vs 1/V
3. PV vs P
Interpret each graph in terms of a law.
Assuming that the pressure values given above are correct, find the correct measurement of the volume.
Solution:

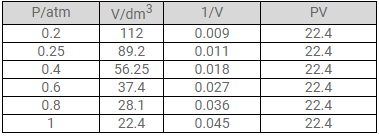
 i. P vs. V:

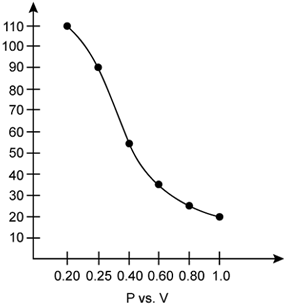
At constant temperature, P is inversely proportional to V. Thus, the plot of V versus P will be a rectangular hyperbola.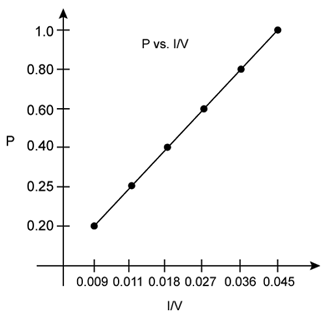

According to Boyle’s law, at constant temperature, pressure of a fixed amount of gas varies inversely to its volume. The graph of pressure verses 1/V shows a positive slope.

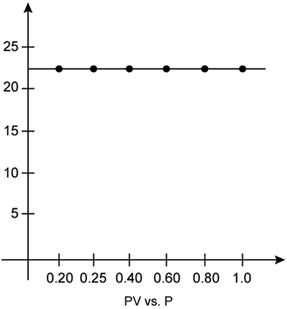
According to Boyle’s law, the product of pressure and volume is constant at constant temperature. The graph of PV versus P is constant which indicates that the given gas obeys Boyle’s law.

b. The correct measurements of the volume are given below:

Question Num 4.
800 cm³ of gas is collected at 650 mm pressure. At what pressure would the volume of the gas reduce by 40% of its original volume, temperature remaining constant?
Solution:

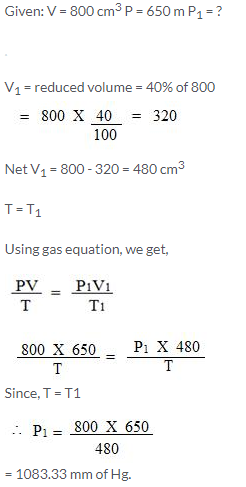
Question Num 5.
A cylinder of 20 litres capacity contains a gas at 100 atmospheric pressure. How many flasks of 200 cm³capacity can be filled from it at 1 atmosphere pressure, temperature remaining constant?
Solution:

Question Num 6.
A steel cylinder of internal volume 20 litres is filled with hydrogen at 29 atmospheric pressure. If hydrogen is used to fill a balloon at 1.25 atmospheric pressure at the same temperature, what volume will the gas occupy?
Solution:

Question Num 7.
561 dm³ of a gas at STP is filled in a 748 dm³ container. If temperature is constant, calculate the percentage change in pressure required.
Solution:
Initial volume = V₁ = 561 dm³
Final volume = V₂ = 748 dm³
Difference in volume = 748 – 561 = 187 dm³
As the temperature is constant,
Decrease in pressure percentage =

Question Num 8.
88 cm³ of nitrogen is at a pressure of 770 mm mercury. If the pressure is raised to 880 mmHg, find by how much the volume will diminish, temperature remaining constant.
Solution:

Question Num 9.
A gas at 240 K is heated to 127°C. Find the percentage change in the volume of the gas (pressure remaining constant).
Solution:

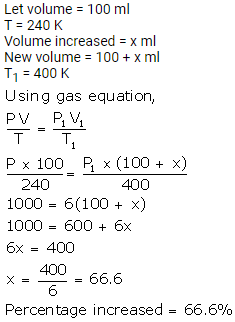
Question Num 10.
Certain amount of a gas occupies a volume of 0.4 litre at 17°C. To what temperature should it be heated so that its volume gets (a) doubled, (b) reduced to half, pressure remaining constant?
Solution:

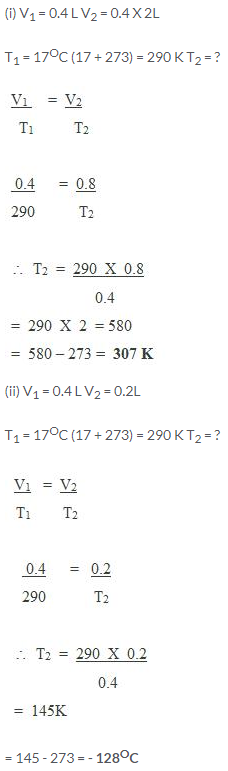
Question Num 11
A gas occupies 3 litres at 0°C. What volume will it occupy at -20°C, pressure remaining constant?
Solution:

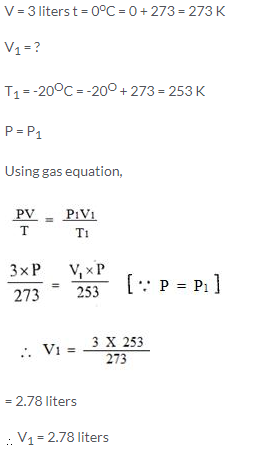
Question Num 12.
A gas occupies 500 cm3 at normal temperature. At what temperature will the volume of the gas be reduced by 20% of its original volume, pressure being constant?
Solution:

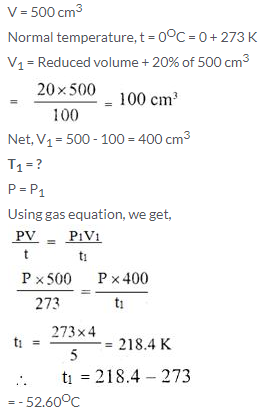
Question Num 13.
Calculate the final volume of a gas ‘X’ if the original pressure of the gas at STP is doubled and its temperature is increased three times.
Solution:

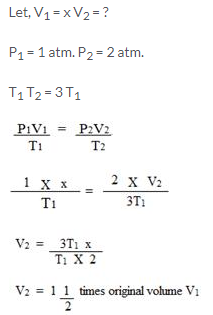
Question Num 14.
A sample of carbon dioxide occupies 30 cm3 at 15°C and 740 mm pressure. Find its volume at STP.
Solution:

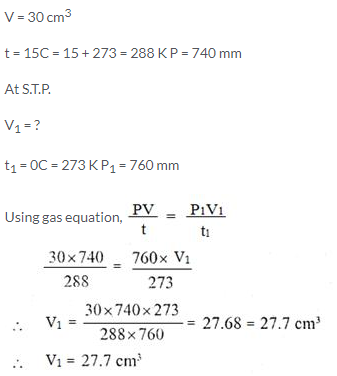
Question Num 15.
50 cm3 of hydrogen is collected over water at 17°C and 750 mmHg pressure. Calculate the volume of a dry gas at STP. The water vapour pressure at 17°C is 14 mmHg.
Solution:

Page No: 124

Question Num 16.
At 0°C and 760 mmHg pressure, a gas occupies a volume of 100 cm³. Kelvin temperature of the gas is increased by one-fifth and the pressure is increased one and a half times. Calculate the final volume of the gas.
Solution:

Question Num 17.
It is found that on heating a gas its volume increases by 50% and its pressure decreases to 60% of its original value. If the original temperature was -15°C, find the temperature to which it was heated.
Solution:

Question Num 18.
A certain mass of a gas occupies 2 litres at 27°C and 100 Pa. Find the temperature when volume and pressure become half of their initial values.
Solution:

Question Num 19
2500 cm3 of hydrogen is taken at STP. The pressure of this gas is further increased by two and a half times (temperature remaining constant). What volume will hydrogen occupy now?
Solution:

Question Num 20.
Taking the volume of hydrogen as calculated in Q.19, what change must be made in Kelvin (absolute) temperature to return the volume to 2500 cm³ (pressure remaining constant)?
Solution:

Question Num 21.
A given amount of gas A is confined in a chamber of constant volume. When the chamber is immersed in a bath of melting ice, the pressure of the gas is 100 cmHg.

1. What is the temperature when the pressure is 10cmHg?
2. What will be the pressure when the chamberis brought to 100°C

Solution:

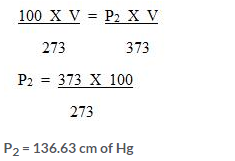
Question Num 22.
A gas is to be filled from a tank of capacity 10,000 litres into cylinders each having capacity of 10 litres. The condition of the gas in the tank is as follows:
a Pressure inside the tank is 800 mmHg.
b. Temperature inside the tank is -3°C.
When the cylinder is filled, the pressure gauge reads 400 mmHg and the temperature is 0°C. Find the number of cylinders required to fill the gas.

Solution 22.

Question Num 23.
Calculate the volume occupied by 2 g of hydrogen at 27°C and 4 atmosphere pressure if at STP it occupies 22.4 litres.
Solution:

Question Num 24.
What temperature would be necessary to double the volume of a gas initially at STP if the pressure is decreased to 50%?
Solution:

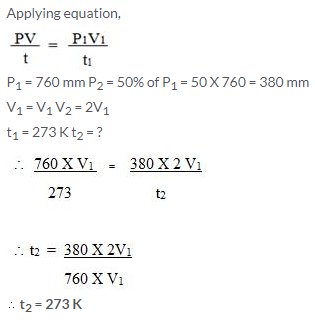
Question Num 25.
Which will have greater volume when the following gases are compared at STP:
1.2/N2 at 25°C and 748 mmHg
1.25/O2 at STP
Solution:

Question Num 26.
Calculate the volume of dry air at STP that occupies 28 cm³ at 14°C and 750 mmHg pressure when saturated with water vapour. The vapour pressure of water at 14°C is 12 mmHg.

Solution:

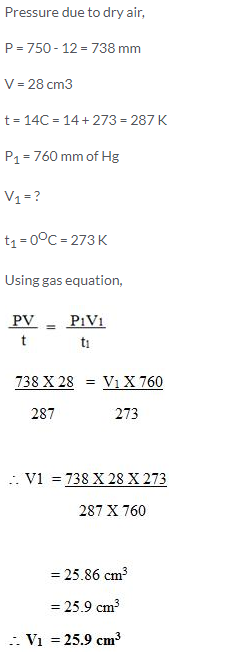
Question Num 27
An LPG cylinder can withstand a pressure of 14.9 atmosphere. The pressure gauge of the cylinder indicates 12 atmosphere at 27°C. Because of a sudden fire in the building, the temperature rises. At what temperature will the cylinder explode?

Solution:
P = 14.9 atm
V = 28 cm³
T = ?
P₁ = 12 atm
V = V₁
]T₁ = 300 K
Using gas equation,

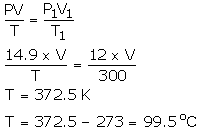
Question Num 28.
22.4 litres of a gas weighs 70 g at STP. Calculate the weight of the gas if it occupies a volume of 20 litres at 27°C and 700 mmHg of pressure.
Solution:

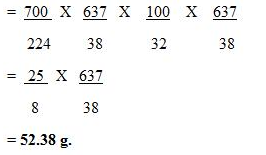
More Resources for Selina Concise Class 9 ICSE Solutions

• Selina ICSE Class 9 Chemistry Solutions
• Selina Class 9 ICSE Physics Solutions
• Selina Concise Biology Class 9 Solutions
• Selina Publishers Mathematics for Class 9