Selina Concise Mathematics Class 10 ICSE Solutions Tangents and Intersecting Chords
Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords
Tangents and Intersecting Chords Exercise 18A – Selina Concise Mathematics Class 10 ICSE Solutions
Question 1.
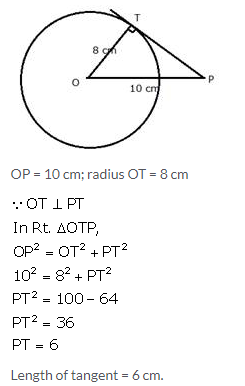
The radius of a circle is 8 cm. Calculate the length of a tangent drawn to this circle from a point at a distance of 10 cm from its centre?
Solution:
Question 2.
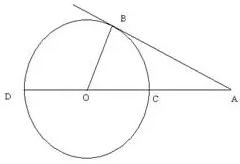
In the given figure, O is the centre of the circle and AB is a tangent to the circle at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
Solution:
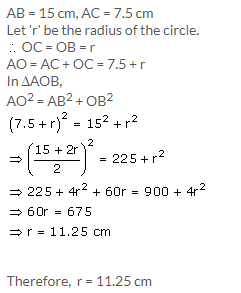
Question 3.
Two circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
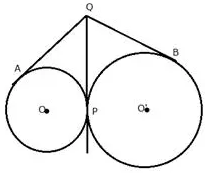
Solution:

Question 4.
Two circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Solution:
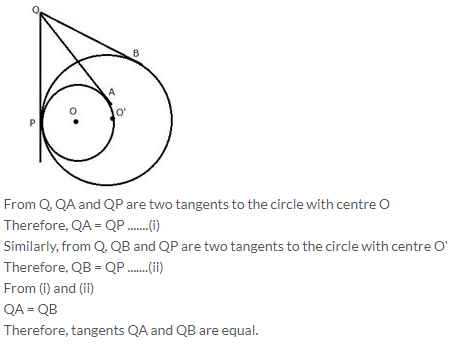
Question 5.
Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
Solution:
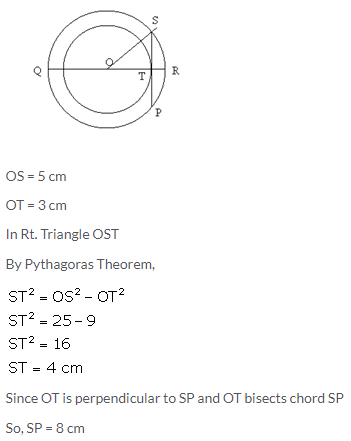
Question 6.
Three circles touch each other externally. A triangle is formed when the centers of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.
Solution:
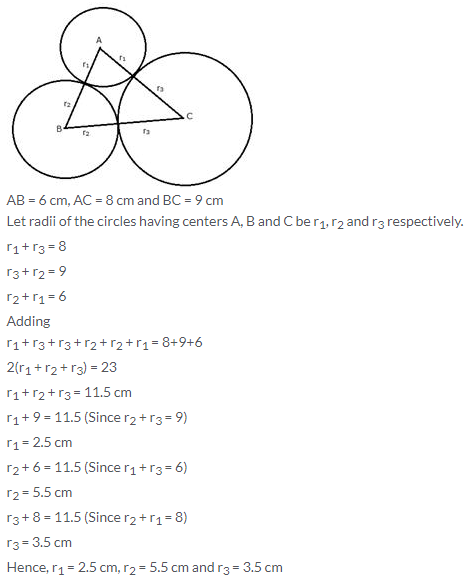
Question 7.
If the sides of a quadrilateral ABCD touch a circle, prove that AB + CD = BC + AD.
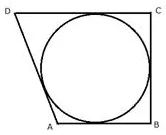
Solution:

Question 8.
If the sides of a parallelogram touch a circle, prove that the parallelogram is a rhombus.
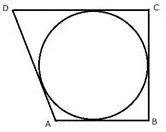
Solution:
From A, AP and AS are tangents to the circle.
Therefore, AP = AS…….(i)
Similarly, we can prove that:
BP = BQ ………(ii)
CR = CQ ………(iii)
DR = DS ………(iv)
Adding,
AP + BP + CR + DR = AS + DS + BQ + CQ
AB + CD = AD + BC
Hence, AB + CD = AD + BC
But AB = CD and BC = AD…….(v) Opposite sides of a ||gm
Therefore, AB + AB = BC + BC
2AB = 2 BC
AB = BC ……..(vi)
From (v) and (vi)
AB = BC = CD = DA
Hence, ABCD is a rhombus.
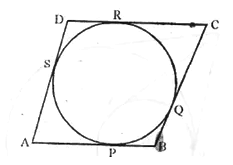
Question 9.
From the given figure prove that:
AP + BQ + CR = BP + CQ + AR.
Also, show that AP + BQ + CR = \(\frac{1}{2}\) × perimeter of triangle ABC.
Solution:

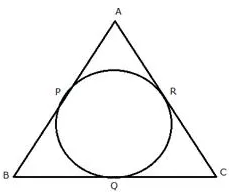
Question 10.
In the figure, if AB = AC then prove that BQ = CQ.
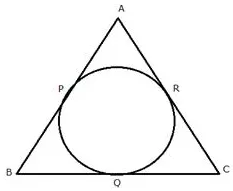
Solution:

Question 11.
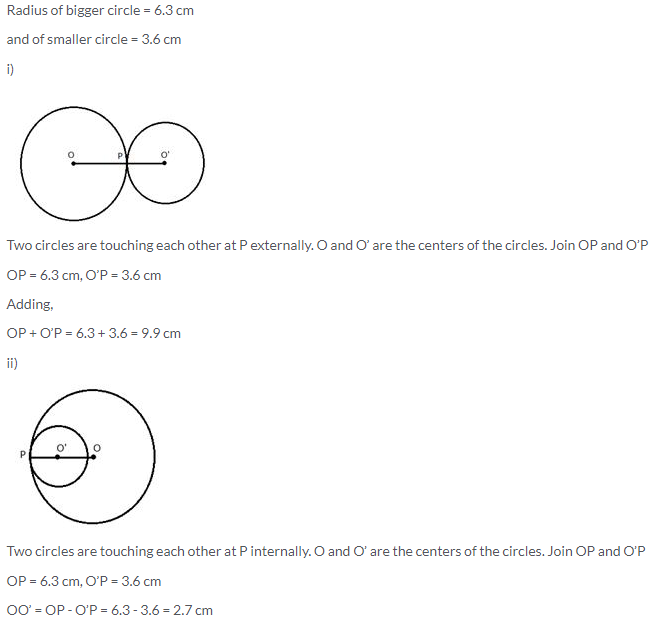
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if –
i) they touch each other externally.
ii) they touch each other internally.
Solution:
Question 12.
From a point P outside the circle, with centre O, tangents PA and PB are drawn. Prove that:
i) ∠AOP = ∠BOP
ii) OP is the perpendicular bisector of chord AB.
Solution:

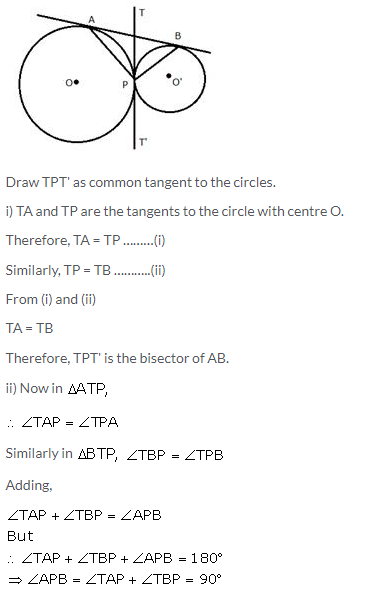
Question 13.
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:

i) tangent at point P bisects AB.
ii) Angle APB = 90°
Solution:
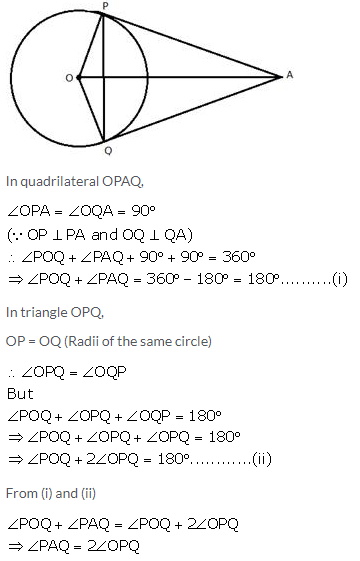
Question 14.
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that:
∠PAQ = 2∠OPQ
Solution:
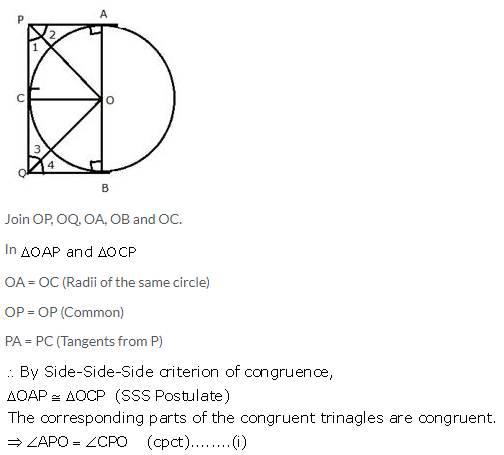
Question 15.
Two parallel tangents of a circle meet a third tangent at point P and Q. Prove that PQ subtends a right angle at the centre.
Solution:

Question 16.
ABC is a right angled triangle with AB = 12 cm and AC = 13 cm. A circle, with centre O, has been inscribed inside the triangle.
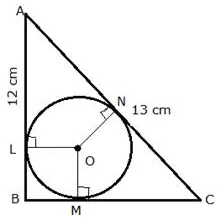
Calculate the value of x, the radius of the inscribed circle.
Solution:
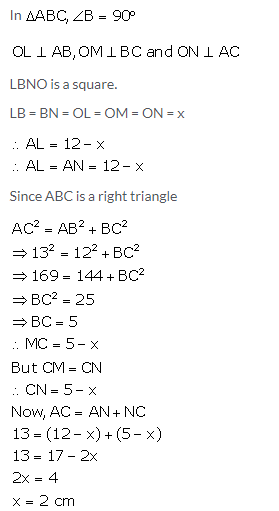
Question 17.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i) ∠QOR
ii) ∠QPR
given that ∠A = 60°
Solution:
Question 18.
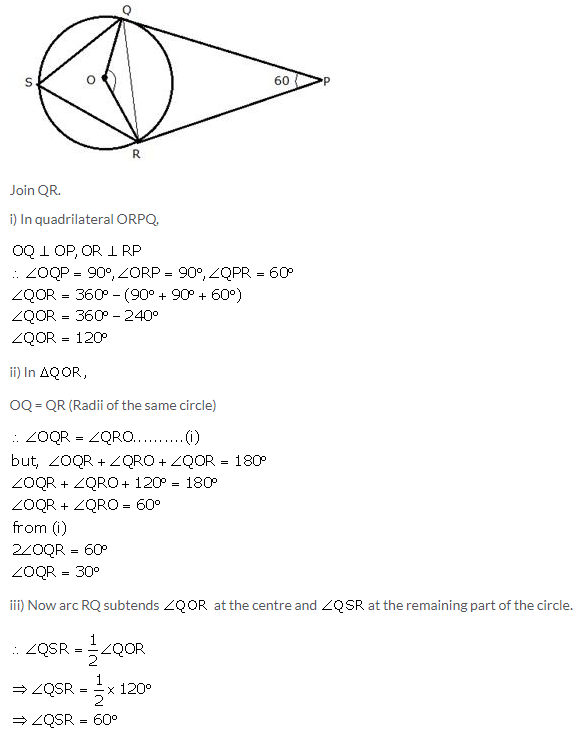
In the following figure, PQ and PR are tangents to the circle, with centre O. If , calculate:
i) ∠QOR
ii) ∠OQR
iii) ∠QSR
Solution:
Question 19.
In the given figure, AB is a diameter of the circle, with centre O, and AT is a tangent. Calculate the numerical value of x.
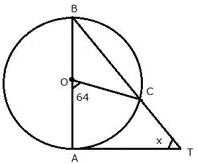
Solution:
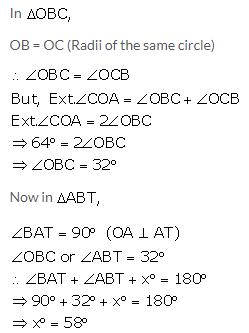
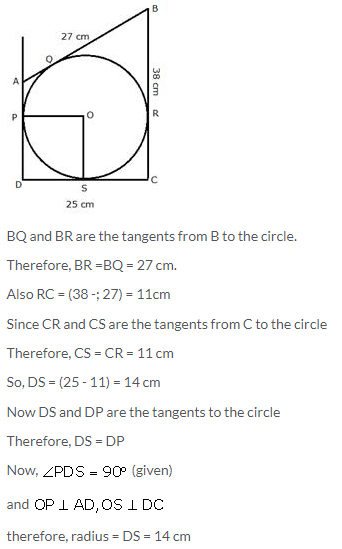
Question 20.
In quadrilateral ABCD, angle D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm. Find the radius of the circle.
Solution:
Question 21.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P.
Given and ∠SPR = x° and ∠QRP = y°
Prove that -;
i) ∠ORS = y°
ii) write an expression connecting x and y
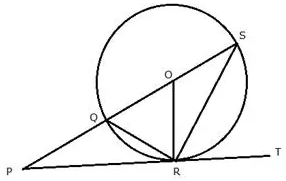
Solution:
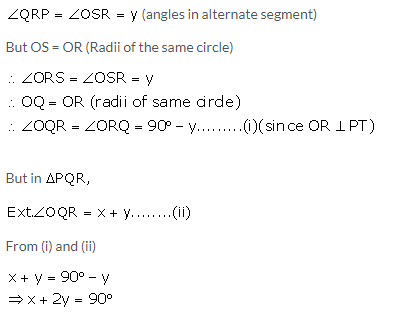
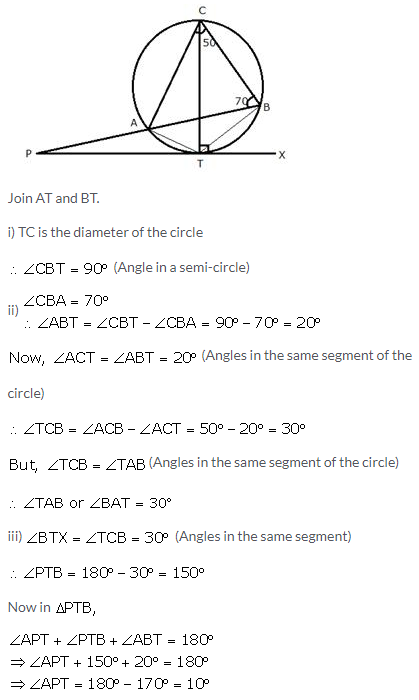
Question 22.
PT is a tangent to the circle at T. If ; calculate:
i) ∠CBT
ii) ∠BAT
iii) ∠APT
Solution:
Question 23.
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.
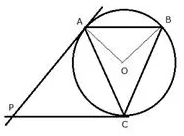
Solution:
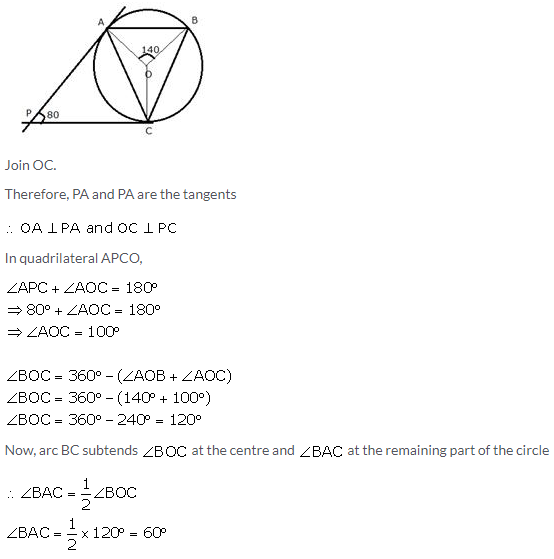
Question 24.
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.

Solution:
∠CAB = ∠BAQ = 30°……(AB is angle bisector of ∠CAQ)
∠CAQ = 2∠BAQ = 60°……(AB is angle bisector of ∠CAQ)
∠CAQ + ∠PAC = 180°……(angles in linear pair)
∴∠PAC = 120°
∠PAC = 2∠CAD……(AD is angle bisector of ∠PAC)
∠CAD = 60°
Now,
∠CAD + ∠CAB = 60 + 30 = 90°
∠DAB = 90°
Thus, BD subtends 90° on the circle
So, BD is the diameter of circle
Tangents and Intersecting Chords Exercise 18B – Selina Concise Mathematics Class 10 ICSE Solutions
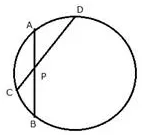
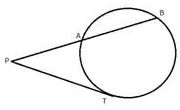
Question 1.
i) In the given figure, 3 x CP = PD = 9 cm and AP = 4.5 cm. Find BP.
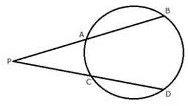
ii) In the given figure, 5 x PA = 3 x AB = 30 cm and PC = 4cm. Find CD.
iii) In the given figure, tangent PT = 12.5 cm and PA = 10 cm; find AB.
Solution:

Question 2.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find
(i) AB.
(ii) the length of tangent PT.

Solution:

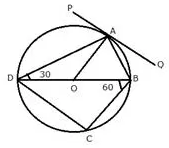
Question 3.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ; ∠ADB = 30° and ∠CBD = 60° calculate:
i) ∠QAD
ii) ∠PAD
iii) ∠CDB
Solution:

Question 4.
If PQ is a tangent to the circle at R; calculate:
i) ∠PRS
ii) ∠ROT
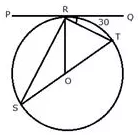
Given: O is the centre of the circle and ∠TRQ = 30°
Solution:

Question 5.
AB is diameter and AC is a chord of a circle with centre O such that angle BAC=30º. The tangent to the circle at C intersects AB produced in D. Show that BC = BD.
Solution:

Question 6.
Tangent at P to the circumcircle of triangle PQR is drawn. If this tangent is parallel to side QR, show that triangle PQR is isosceles.
Solution:

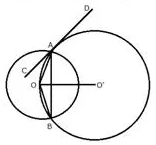
Question 7.
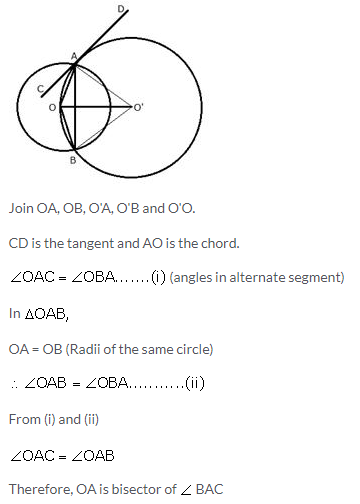
Two circles with centers O and O’ are drawn to intersect each other at points A and B.
Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O’ at A. Prove that OA bisects angle BAC.
Solution:

Question 8.
Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that: ∠CPA = ∠DPB
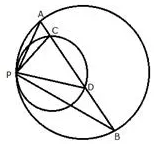
Solution:
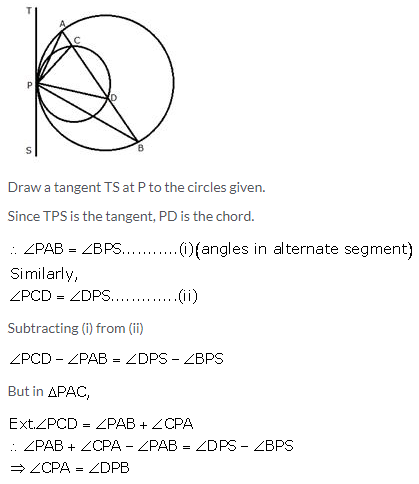
Question 9.
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
Solution:
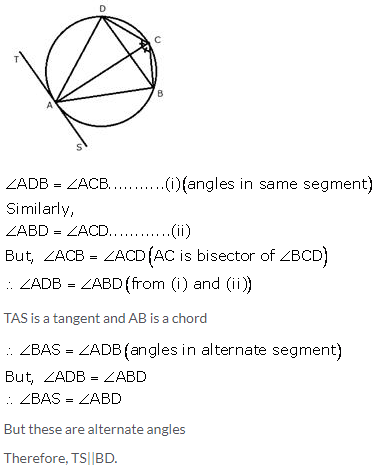
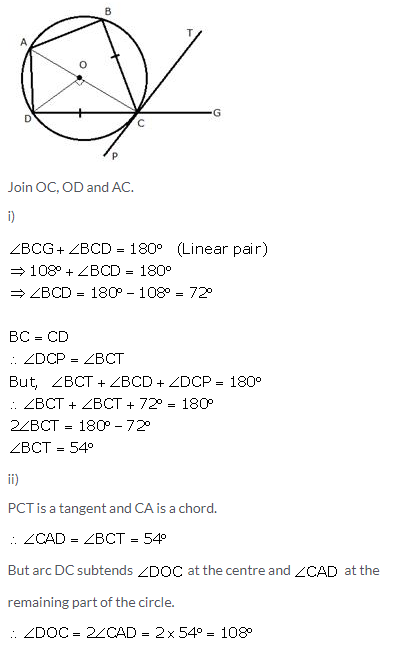
Question 10.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG = 108° and O is the centre of the circle, find:
i) angle BCT
ii) angle DOC

Solution:
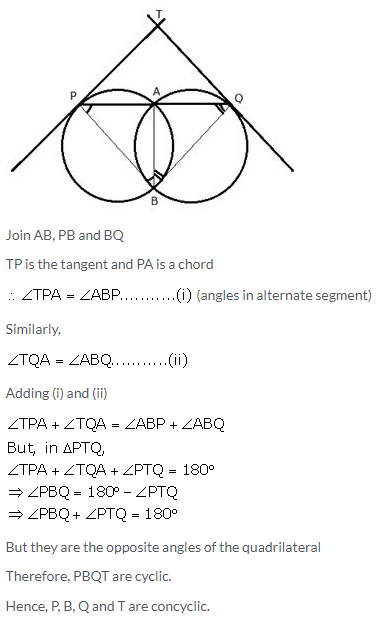
Question 11.
Two circles intersect each other at point A and B. A straight line PAQ cuts the circle at P and Q. If the tangents at P and Q intersect at point T; show that the points P, B, Q and T are concyclic.
Solution:
Question 12.
In the figure, PA is a tangent to the circle. PBC is a secant and AD bisects angle BAC.
Show that the triangle PAD is an isosceles triangle. Also show that:
∠CAD = \(\frac{1}{2}\)(∠PBA – ∠PAB)
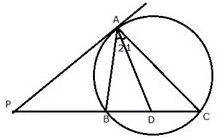
Solution:

Question 13.
Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
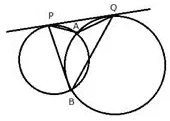
Solution:

Question 14.
In the figure, chords AE and BC intersect each other at point D.
i) if , ∠CDE = 90° AB = 5 cm, BD = 4 cm and CD = 9 cm; find DE
ii) If AD = BD, Show that AE = BC.

Solution:

Question 15.
Circles with centers P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles are congruent; show that CE = BD.
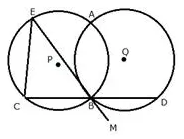
Solution:

Question 16.
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. Find ∠BDC = 65. Find ∠BAO
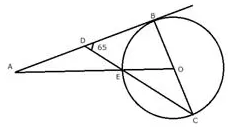
Solution:

Tangents and Intersecting Chords Exercise 18C – Selina Concise Mathematics Class 10 ICSE Solutions
Question 1.
Prove that of any two chord of a circle, the greater chord is nearer to the centre.
Solution:
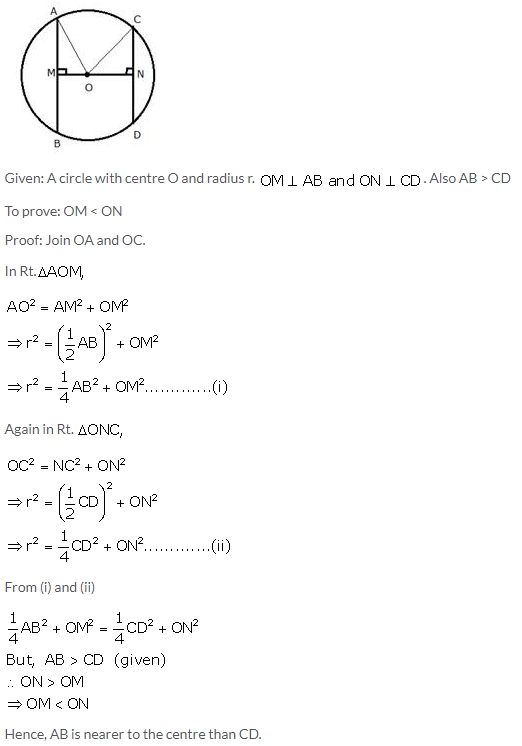
Question 2.
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O.
i) If the radius of the circle is 10 cm, find the area of the rhombus.
ii) If the area of the rhombus is \(32 \sqrt{3}\) cm2, find the radius of the circle.
Solution:
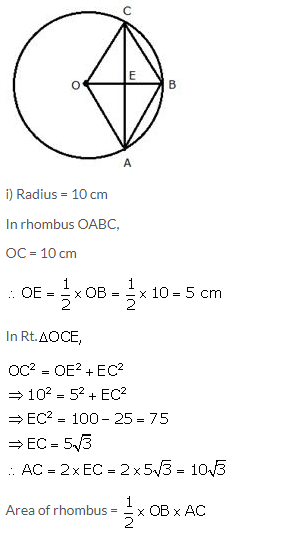

Question 3.
Two circles with centers A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
Solution:

Question 4.
Two chords AB and AC of a circle are equal. Prove that the centre of the circle, lies on the bisector of the angle BAC.
Solution:

Question 5.
The diameter and a chord of circle have a common end-point. If the length of the diameter is 20 cm and the length of the chord is 12 cm, how far is the chord from the centre of the circle?
Solution:
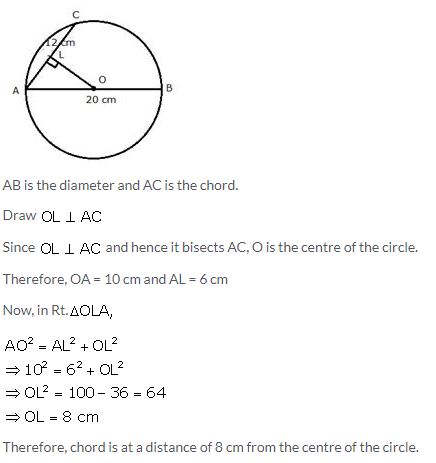
Question 6.
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
Solution:

Question 7.
In the given figure, C and D are points on the semicircle described on AB as diameter.
Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC
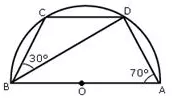
Solution:

Question 8.
In cyclic quadrilateral ABCD, ∠A = 3 ∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
Solution:

ABCD is a cyclic quadrilateral.
∴ ∠A + ∠C = 180°
⇒ 3∠C + ∠C = 180°
⇒ 4∠C = 180°
⇒ ∠C = 45°
∵ ∠A = 3∠C
⇒ ∠A = 3 × 45°
⇒ ∠A = 135°
Similarly,
∴ ∠B+ ∠D = 180°
⇒∠B + 5∠B = 180°
⇒ 6∠B = 180°
⇒ ∠B = 30°
∵∠D = 5∠B
⇒ ∠D = 5 × 30° >
⇒ ∠D = 150°
Hence, ∠A = 1350, ∠B = 30°, ∠C = 450, ∠D = 150°
Question 9.
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Solution:
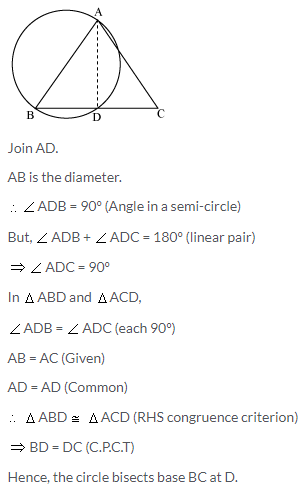
Question 10.
Bisectors of vertex A, B and C of a triangle ABC intersect its circumcircle at points D, E and F respectively. Prove that angle EDF = \(90^{\circ}-\frac{1}{2} \angle A\)
Solution:
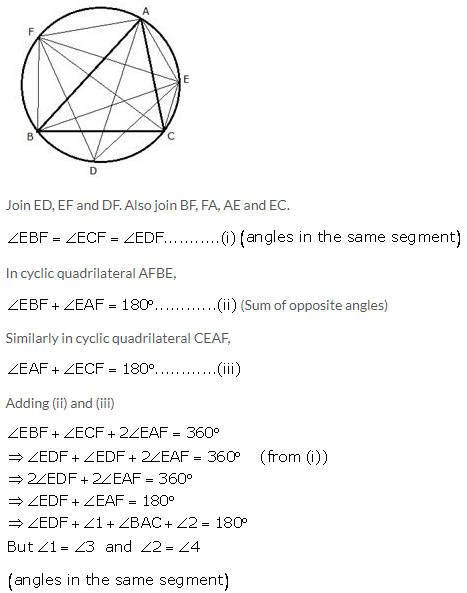
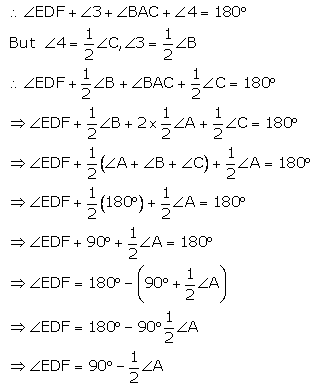
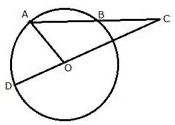
Question 11.
In the figure, AB is the chord of a circle with centre O and DOC is a line segment such that BC = DO. If ∠C = 20°, find angle AOD.
Solution:

Question 12.
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
Solution:

Question 13.
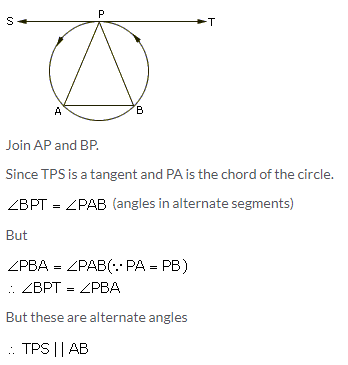
P is the midpoint of an arc APB of a circle. Prove that the tangent drawn at P will be parallel to the chord AB.
Solution:
Question 14.
In the given figure, MN is the common chord of two intersecting circles and AB is their common tangent.
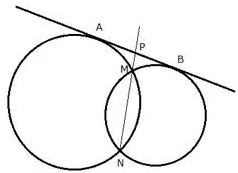
Prove that the line NM produced bisects AB at P.
Solution:

Question 15.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find:
i) ∠DBC
ii) ∠ BCP
iii) ∠ ADB
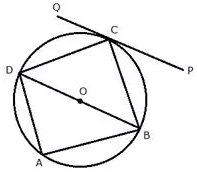
Solution:

Question 16.
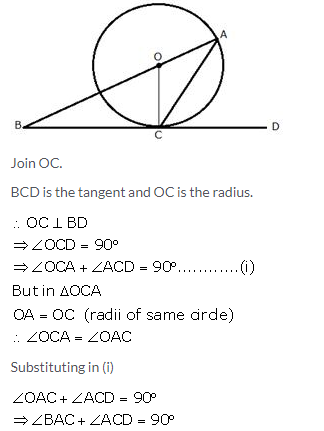
The given figure shows a circle with centre O and BCD is a tangent to it at C. Show that: ∠ACD + ∠BAC = 90°
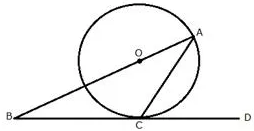
Solution:
Question 17.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D.
Prove that –
i) AC × AD = AB2
ii) BD2 = AD × DC.
Solution:

Question 18.
In the given figure AC = AE.
Show that:
i) CP = EP
ii) BP = DP
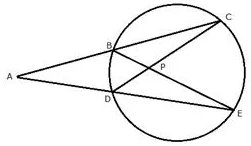
Solution:

Question 19.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°
Calculate:
i) ∠BEC
ii) ∠ BED
Solution:
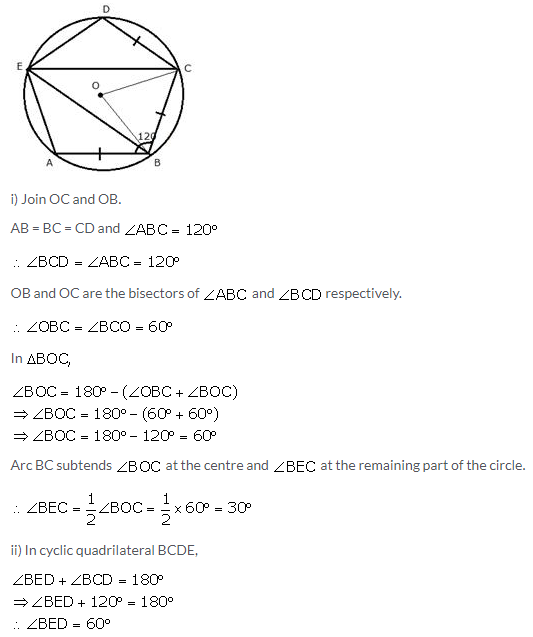
Question 20.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find:
(i) angle BCO
(ii) angle AOB
(iii) angle APB
Solution:

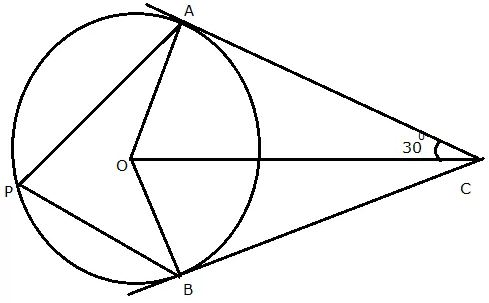
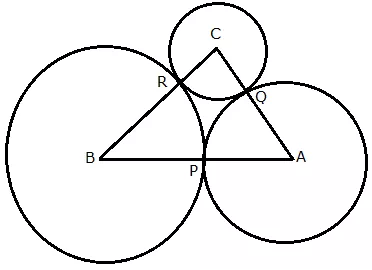
Question 21.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
Solution:

Question 22.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that –
i) ∠ONL + ∠OML = 180°
ii) ∠BAM = ∠BMA
iii) ALOB is a cyclic quadrilateral.
Solution:

Question 23.
The given figure shows a semicircle with centre O and diameter PQ. If PA = AB and ∠BOQ = 140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
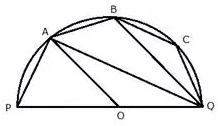
Solution:


Question 24.
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°.
Calculate –
i) angle QTR
ii) angle QRP
iii) angle QRS
iv) angle STR
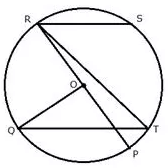
Solution:


Question 25.
In the given figure, PAT is tangent to the circle with centre O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
i) ∠BAP = ∠ADQ
ii) ∠AOB = 2∠ADQ
(iii) ∠ADQ = ∠ADB.
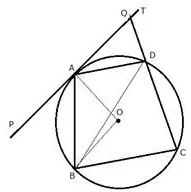
Solution:

Question 26.
AB is a line segment and M is its midpoint. Three semicircles are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r unit is drawn so that it touches all the three semicircles. Show that: AB = 6 x r
Solution:
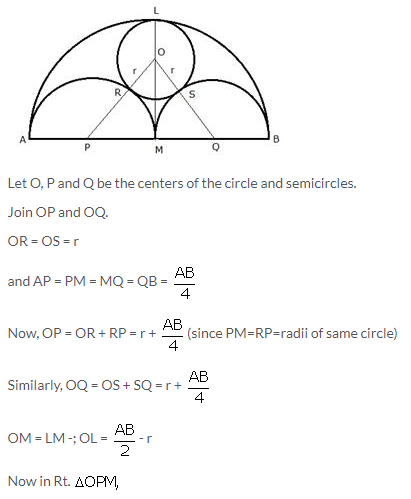
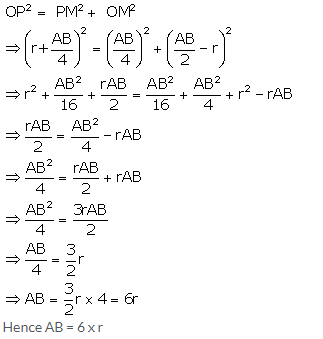
Question 27.
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
Solution:

Question 28.
Two circles intersect in points P and Q. A secant passing through P intersects the circle in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
Solution:
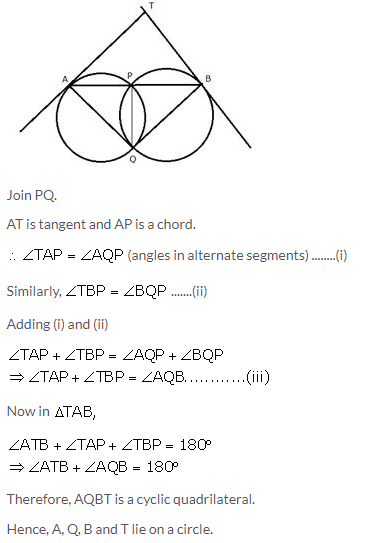
Question 29.
Prove that any four vertices of a regular pentagon are concyclic (lie on the same circle)
Solution:

Question 30.
Chords AB and CD of a circle when extended meet at point X. Given AB = 4 cm, BX = 6 cm and XD = 5 cm. Calculate the length of CD.
Solution:
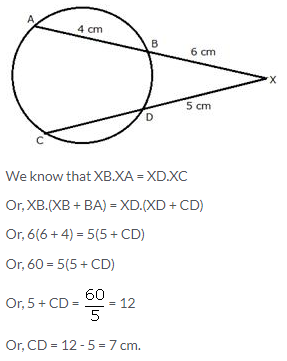
Question 31.
In the given figure, find TP if AT = 16 cm and AB = 12 cm.
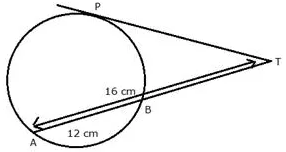
Solution:
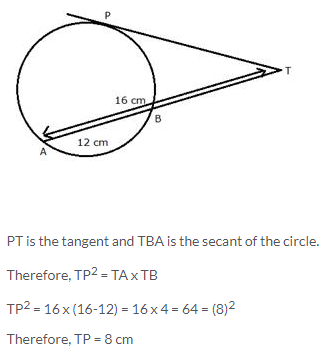
Question 32.
In the following figure, A circle is inscribed in the quadrilateral ABCD.
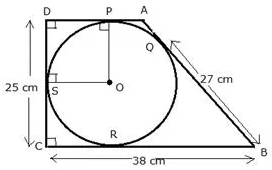
If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
Solution:

Question 33.
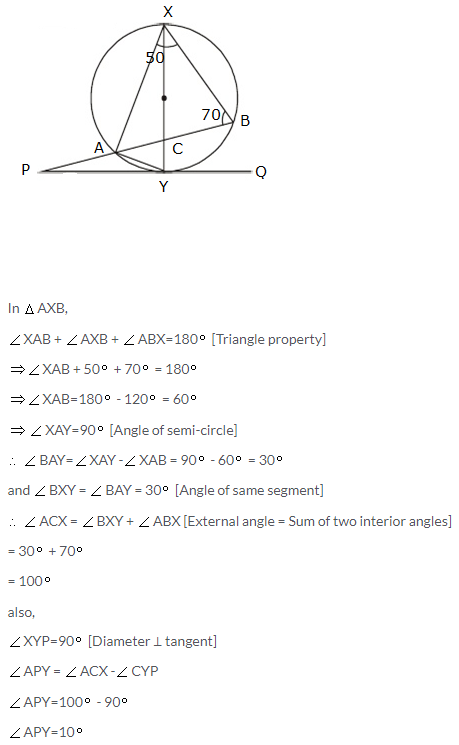
In the figure, XY is the diameter of the circle, PQ is the tangent to the circle at Y. Given that ∠AXB = 50° and ∠ABX = 70°. Calculate ∠BAY and ∠APY.

Solution:
Question 34.
In the given figure, QAP is the tangent at point A and PBD is a straight line. If ∠ACB = 36° and ∠APB = 42°; find:
i) ∠BAP
ii) ∠ABD
iii) ∠QAD
iv) ∠BCD
Solution:

Question 35.
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If
∠CAB = 34°, find
i) ∠CBA
ii) ∠CQB
Solution:
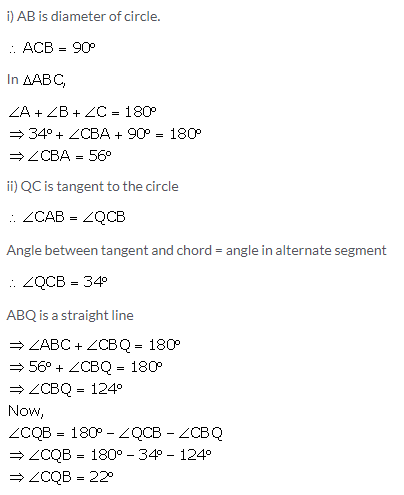
Question 36.
In the given figure, O is the centre of the circle. The tangets at B and D intersect each other at point P.
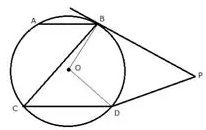
If AB is parallel to CD and ∠ABC = 55°, find:
i) ∠BOD
ii) ∠BPD
Solution:

Question 37.
In the figure given below PQ =QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O. Calculate the values of:
i) ∠QOP
ii) ∠QCP
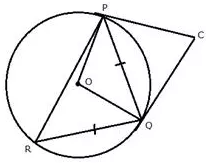
Solution:

Question 38.
In two concentric circles prove that all chords of the outer circle, which touch the inner circle, are of equal length.
Solution:

Question 39.
In the figure, given below, AC is a transverse common tangent to two circles with centers P and Q and of radii 6 cm and 3 cm respectively.
Given that AB = 8 cm, calculate PQ.
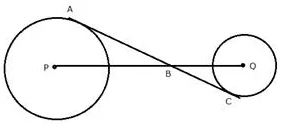
Solution:

Question 40.
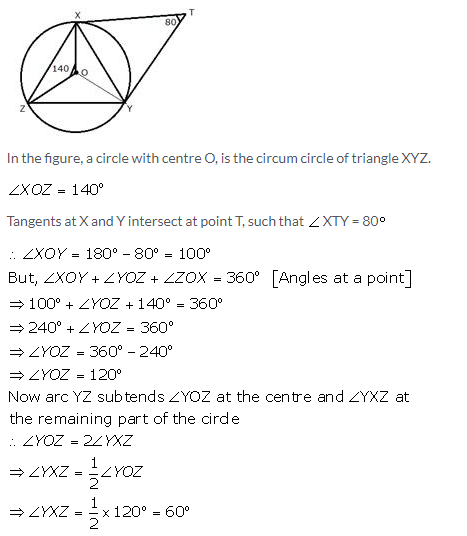
In the figure given below, O is the centre of the circum circle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
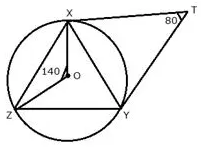
Solution:
Question 41.
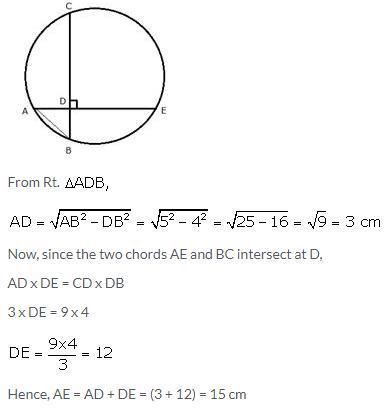
In the given figure, AE and BC intersect each other at point D. If ∠CDE=90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.
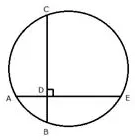
Solution:
Question 42.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
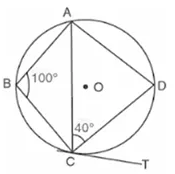
Solution:

Question 43.
In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.
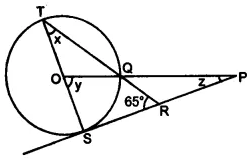
Solution:

More Resources for Selina Concise Class 10 ICSE Solutions
- Selina Maths Class 10 ICSE Solutions
- Selina ICSE Physics Class 10 Solutions
- Concise Chemistry Class 10 ICSE Guide Pdf
- Selina ICSE Class 10 Biology Solutions
ICSE Solutions Selina ICSE Solutions