Selina Concise Mathematics Class 10 ICSE Solutions Loci (Locus and Its Constructions)

Selina Concise Mathematics Class 10 ICSE Solutions Loci (Locus and Its Constructions)

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions)

Locus and Its Constructions Exercise 16A – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Given— PQ is perpendicular bisector of side AB of the triangle ABC.

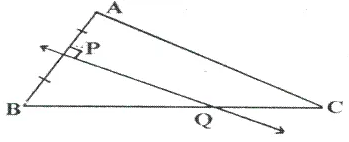
Prove— Q is equidistant from A and B.
Solution:

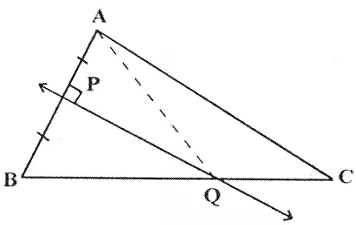
Construction: Join AQ
Proof: In ∆AQP and ∆BQP,
AP = BP (given)
∠QPA = ∠QPB (Each = 90 )
PQ = PQ (Common)
By Side-Angle-Side criterian of congruence, we have
∆AQP ≅ ∆BQP (SAS postulate)
The corresponding parts of the triangle are congruent
∴ AQ = BQ (CPCT)
Hence Q is equidistant from A and B.

Question 2.
Given— CP is bisector of angle C of ∆ ABC.

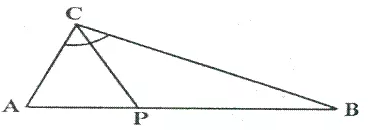
Prove— P is equidistant from AC and BC.
Solution:

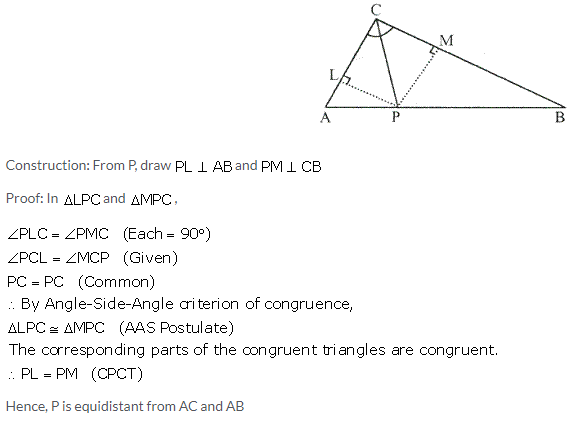
Question 3.
Given— AX bisects angle BAG and PQ is perpendicular bisector of AC which meets AX at point Y.

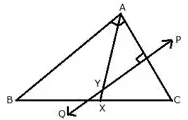
Prove—
(i) X is equidistant from AB and AC.
(ii) Y is equidistant from A and C.
Solution:

Question 4.
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
Solution:
Given: In triangle ABC, AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm

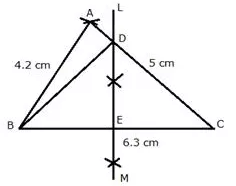
Steps of Construction:
i) Draw a line segment BC = 6.3 cm
ii) With centre B and radius 4.2 cm, draw an arc.
iii) With centre C and radius 5 cm, draw another arc which intersects the first arc at A.
iv) Join AB and AC.
∆ABC is the required triangle.
v) Again with centre B and C and radius greater than \(\frac{1}{2} \mathrm{BC}\) draw arcs which intersects each other at L and M.
vi) Join LM intersecting AC at D and BC at E.
vii) Join DB.

Hence, D is equidistant from B and C.

Question 5.
In each of the given figures: PA = PH and QA = QB.

Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of points equidistant from two given fixed points.
Solution:
Construction: Join PQ which meets AB in D.

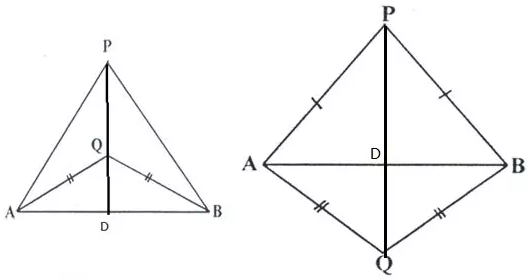
Proof: P is equidistant from A and B.
∴ P lies on the perpendicular bisector of AB.
Similarly, Q is equidistant from A and B.
∴ Q lies on perpendicular bisector of AB.
∴ P and Q both lie on the perpendicular bisector of AB.
∴ PQ is perpendicular bisector of AB.
Hence, locus of the points which are equidistant from two fixed points, is a perpendicular bisector of the line joining the fixed points.

Question 6.
Construct a right angled triangle PQR, in which ∠ Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Solution:

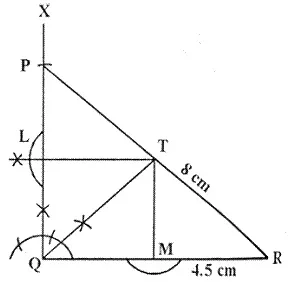
Steps of Construction:
i) Draw a line segment QR = 4.5 cm
ii) At Q, draw a ray QX making an angle of 90°
iii) With centre R and radius 8 cm, draw an arc which intersects QX at P.
iv) Join RP.
∆PQR is the required triangle.
v) Draw the bisector of ∠PQR which meets PR in T.
vi) From T, draw perpendicular PL and PM respectively on PQ and QR.

Hence, T is equidistant from PQ and QR.

Question 7.
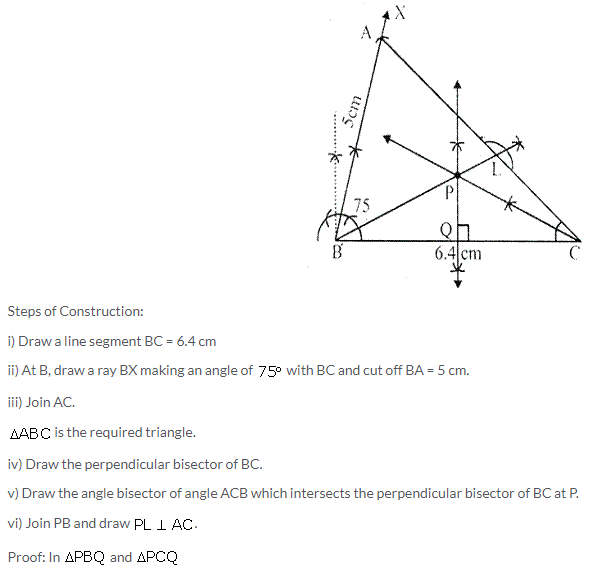
Construct a triangle ABC in which angle ABC = 75°. AB = 5 cm and BC = 6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P ; prove that P is equidistant from B and C ; and also from AC and BC.
Hence P is equidistant from AC and BC.
Solution:

Question 8.
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
Solution:

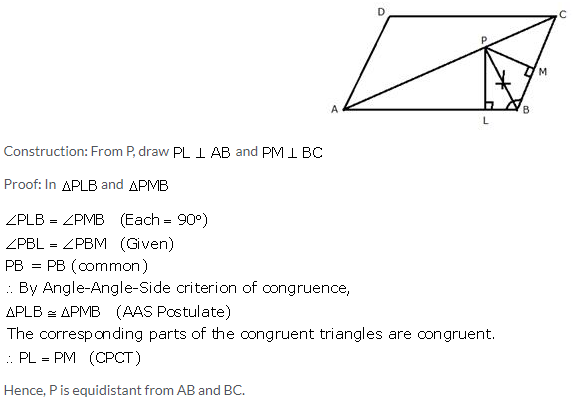
Question 9.
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A.
Prove that –
(i) point A is equidistant from all the three sides of the triangle.
(ii) AM bisects angle LMN.
Solution:

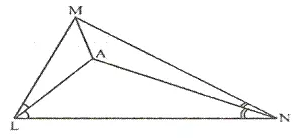
Construction: Join AM
Proof:
∵ A lies on bisector of ∠N
∴A is equidistant from MN and LN.
Again, A lies on bisector of ∠L
∴ A is equidistant from LN and LM.
Hence, A is equidistant from all sides of the triangle LMN.
∴ A lies on the bisector of ∠M

Question 10.
Use ruler and compasses only for this question:
(i) construct ∆ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
Solution:
Steps of construction:
(i) Draw line BC = 6 cm and an angle CBX = 60o. Cut off AB = 3.5. Join AC, triangle ABC is the required triangle.
(ii) Draw perpendicular bisector of BC and bisector of angle B
(iii) Bisector of angle B meets bisector of BC at P.
⇒ BP is the required length, where, PB = 3.5 cm
(iv) P is the point which is equidistant from BA and BC, also equidistant from B and C.

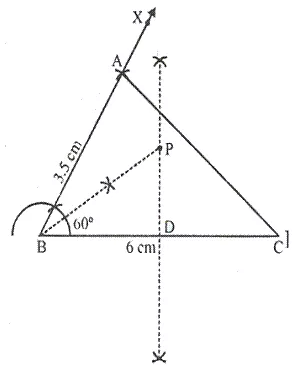
PB=3.6 cm

Question 11.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point E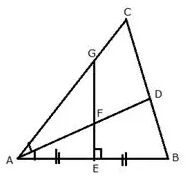
Prove that:
(i) F is equidistant from A and B.
(ii) F is equidistant from AB and AC.
Solution:

Question 12.
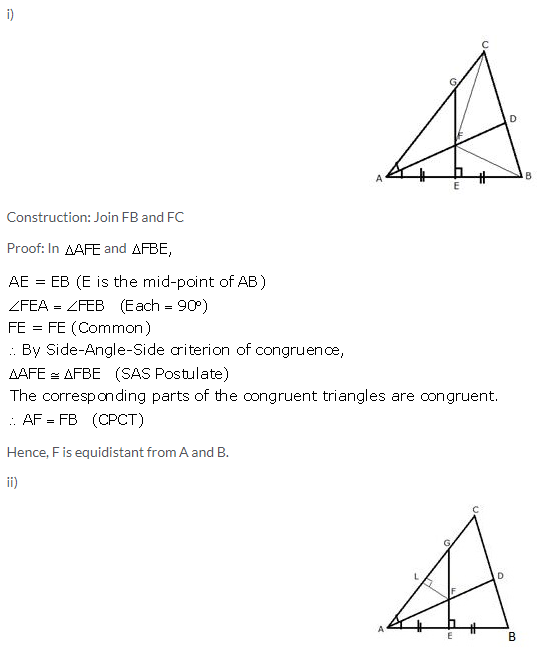
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect each other at point P. Show that P is equidistant from the opposite sides AB and CD.
Solution:

Since P lies on the bisector of angle B,
therefore, P is equidistant from AB and BC …. (1)
Similarly, P lies on the bisector of angle C,
therefore, P is equidistant from BC and CD …. (2)
From (1) and (2),
Hence, P is equidistant from AB and CD.

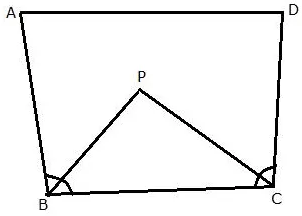
Question 13.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Solution:

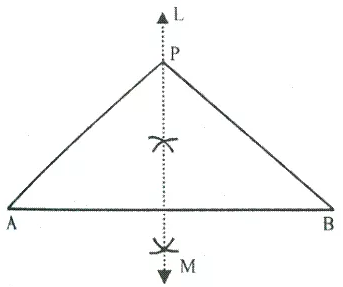
Steps of construction:
(i) Draw a line segment AB of 6 cm.
(ii) Draw perpendicular bisector LM of AB. LM is the required locus.
(iii) Take any point on LM say P.
(iv) Join PA and PB.
Since, P lies on the right bisector of line AB.
Therefore, P is equidistant from A and B.
i.e. PA = PB
Hence, Perpendicular bisector of AB is the locus of all points which are equidistant from A and B.

Question 14.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
Solution:

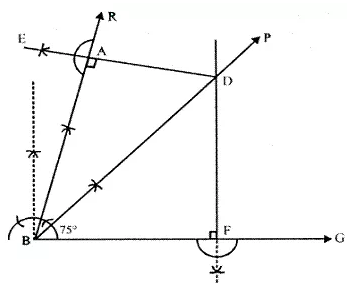
Steps of Construction:
i) Draw a ray BC.
ii) Construct a ray RA making an angle of 75° with BC. Therefore, ABC= 75°.
iii) Draw the angle bisector BP of ∠ABC.
BP is the required locus.
iv) Take any point D on BP.
v) From D, draw DE ⊥ AB and DF ⊥ BC
Since D lies on the angle bisector BP of ∠ABC
D is equidistant from AB and BC.
Hence, DE = DF
Similarly, any point on BP is equidistant from AB and BC.
Therefore, BP is the locus of all points which are equidistant from AB and BC.

Question 15.
Draw an angle ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC ; and also equidistant from A and B.
Solution:

Steps of Construction:
i) Draw a line segment BC = 5 cm
ii) At B, draw a ray BX making an angle of 60° and cut off BA = 4.6 cm.
iii) Draw the angle bisector of ∠ABC.
iv) Draw the perpendicular bisector of AB which intersects the angle bisector at P.
P is the required point which is equidistant from AB and BC, as well as from A and B.

Question 16.
In the figure given below, find a point P on CD equidistant from points A and B.

Solution:

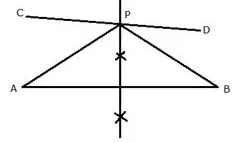
Steps of Construction:
i) AB and CD are the two lines given.
ii) Draw a perpendicular bisector of line AB which intersects CD in P.
P is the required point which is equidistant from A and B.
Since P lies on perpendicular bisector of AB; PA = PB.

Question 17.
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.

Solution:

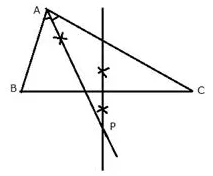
Steps of Construction:
i) In the given triangle, draw the angle bisector of ∠BAC.
ii) Draw the perpendicular bisector of BC which intersects the angle bisector at P.
P is the required point which is equidistant from AB and AC as well as from B and C.
Since P lies on angle bisector of ∠BAC,
It is equidistant from AB and AC.
Again, P lies on perpendicular bisector of BC,
Therefore, it is equidistant from B and C.

Question 18.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ ABC = 60°. Locate by construction the point P such that :
(i) P is equidistant from B and C.
(ii) P is equidistant from AB and BC.
(iii) Measure and record the length of PB.

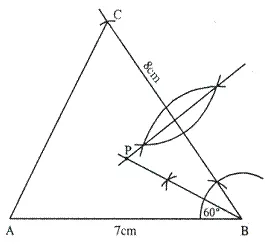
Solution:
Steps of Construction:
1) Draw a line segment AB = 7 cm.
2) Draw angle ∠ABC = 60° with the help of compass.
3) Cut off BC = 8 cm.
4) Join A and C.
5) The triangle ABC so formed is the required triangle.
i) Draw the perpendicular bisector of BC. The point situated on this line will be equidistant from B and C.
ii) Draw the angle bisector of ∠ABC. Any point situated on this angular bisector is equidistant from lines AB and BC.
The point which fulfills the condition required in (i) and (ii) is the intersection point of bisector of line BC and angular bisector of ∠ABC.
P is the required point which is equidistant from AB and AC as well as from B and C.
On measuring the length of line segment PB, it is equal to 4.5 cm.

Question 19.
On a graph paper, draw lines x = 3 and y = -5. Now, on the same graph paper, draw the locus of the point which is equidistant from the given lines.
Solution:

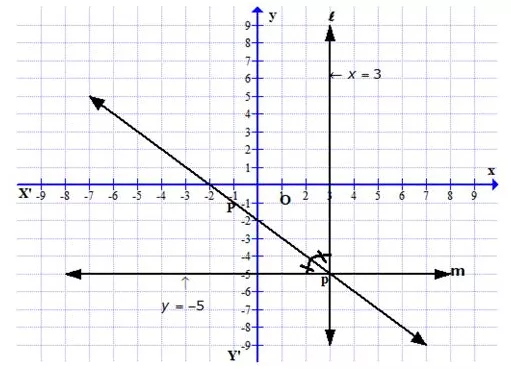
On the graph, draw axis XOX’ and YOY’
Draw a line l, x = 3 which is parallel to y-axis
And draw another line m, y = -5, which is parallel to x-axis
These two lines intersect each other at P.
Now draw the angle bisector p of angle P.
Since p is the angle bisector of P, any point on P is equidistant from l and m.
Therefore, this line p is equidistant from l and m.

Question 20.
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distance from the given line is always equal to 3 units.
Solution:

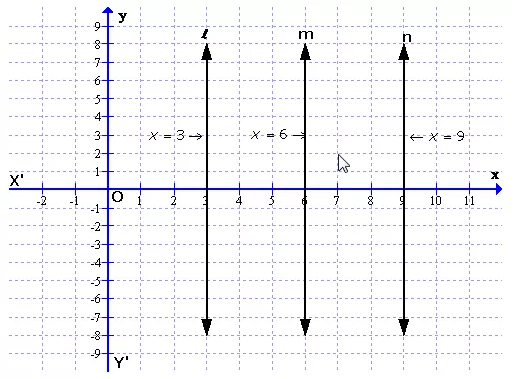
On the graph, draw axis XOX’ and YOY’
Draw a line l, x = 6 which is parallel to y-axis
Take points P and Q which are at a distance of 3 units from the line l.
Draw lines m and n from P and Q parallel to l
With locus = 3, two lines can be drawn x = 3 and x = 9.

Locus and Its Constructions Exercise 16B – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Describe the locus of a point at a distance of 3 cm from a fixed point.
Solution:

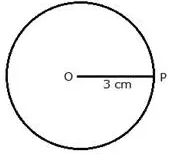
The locus of a point which is 3 cm away from a fixed point is circumference of a circle whose radius is 3 cm and the fixed point is the centre of the circle.

Question 2.
Describe the locus of a point at a distance of 2 cm from a fixed line.
Solution:

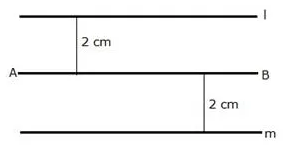
The locus of a point at a distance of 2 cm from a fixed line AB is a pair of straight lines l and m which are parallel to the given line at a distance of 2 cm.

Question 3.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Solution:

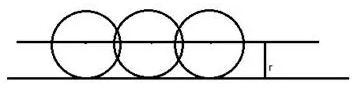
The locus of the centre of a wheel, which is going straight along a level road will be a straight line parallel to the road at a distance equal to the radius of the wheel.

Question 4.
Describe the locus of the moving end of the minute hand of a clock.
Solution:

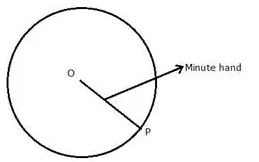
The locus of the moving end of the minute hand of the clock will be a circle where radius will be the length of the minute hand.

Question 5.
Describe the locus of a stone dropped from the top of a tower.
Solution:

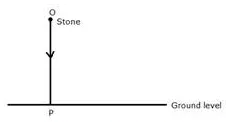
The locus of a stone which is dropped from the top of a tower will be a vertical line through the point from which the stone is dropped.

Question 6.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Solution:

The locus of the runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge will be the circumference of a circle whose radius is equal to the radius of the inner circular track plus 1.5 m.

Question 7.
Describe the locus of the door handle as the door opens.
Solution:

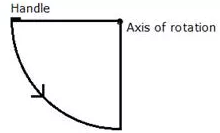
The locus of the door handle will be the circumference of a circle with centre at the axis of rotation of the door and radius equal to the distance between the door handle and the axis of rotation of the door.

Question 8.
Describe the locus of a point inside a circle and equidistant from two fixed points on the circumference of the circle.
Solution:

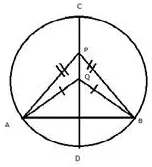
The locus of the points inside the circle which are equidistant from the fixed points on the circumference of a circle will be the diameter which is perpendicular bisector of the line joining the two fixed points on the circle.

Question 9.
Describe the locus of the centers of all circles passing through two fixed points.
Solution:

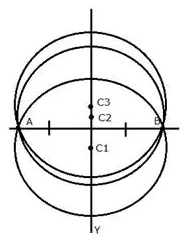
The locus of the centre of all the circles which pass through two fixed points will be the perpendicular bisector of the line segment joining the two given fixed points.

Question 10.
Describe the locus of vertices of all isosceles triangles having a common base.
Solution:

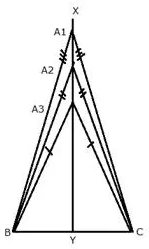
The locus of vertices of all isosceles triangles having a common base will be the perpendicular bisector of the common base of the triangles.

Question 11.
Describe the locus of a point in space which is always at a distance of 4 cm from a fixed point.
Solution:
The locus of a point in space is the surface of the sphere whose centre is the fixed point and radius equal to 4 cm.

Question 12.
Describe the locus of a point P so that:
AB² = AP² + BP², where A and B are two fixed points.
Solution:

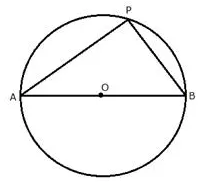
The locus of the point P is the circumference of a circle with AB as diameter and satisfies the condition AB² = AP² + BP².

Question 13.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
i) AB and BC
ii) B and D.
Solution:
i)

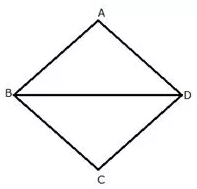
The locus of the point in a rhombus ABCD which is equidistant from AB and BC will be the diagonal BD.
ii)

The locus of the point in a rhombus ABCD which is equidistant from B and D will be the diagonal AC.

Question 14.
The speed of sound is 332 meters per second. A gun is fired. Describe the locus of all the people on the Earth’s surface, who hear the sound exactly one second later.
Solution:
The locus of all the people on Earth’s surface is the circumference of a circle whose radius is 332 m and centre is the point where the gun is fired.

Question 15.
Describe:
i) The locus of points at distances less than 3 cm from a given point.
ii) The locus of points at distances greater than 4 cm from a given point.
iii) The locus of points at distances less than or equal to 2.5 cm from a given point.
iv) The locus of points at distances greater than or equal to 35 mm from a given point.
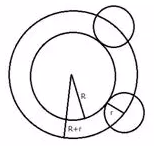
v)The locus of the centre of a given circle which rolls around the outside of a second circle and is always touching it.
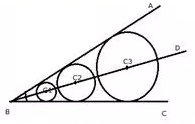
vi) The locus of the centers of all circles that are tangent to both the arms of a given angle.
vii) The locus of the mid-points of all chords parallel to a given chord of a circle.
viii) The locus of points within a circle that are equidistant from the end points of a given chord.
Solution:
i) The locus is the space inside of the circle whose radius is 3 cm and the centre is the fixed point which is given.
ii) The locus is the space outside of the circle whose radius is 4 cm and centre is the fixed point which is given.
iii) The locus is the space inside and circumference of the circle with a radius of 2.5 cm and the centre is the given fixed point.
iv) The locus is the space outside and circumference of the circle with a radius of 35 mm and the centre is the given fixed point.
v) The locus is the circumference of the circle concentric with the second circle whose radius is equal to the sum of the radii of the two given circles.

vi) The locus of the centre of all circles whose tangents are the arms of a given angle is the bisector of that angle.

vii) The locus of the mid-points of the chords which are parallel to a given chords is the diameter perpendicular to the given chords.

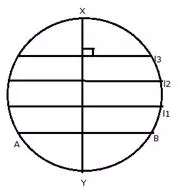
viii) The locus of the points within a circle which are equidistant from the end points of a given chord is the diameter which is perpendicular bisector of the given chord.

Question 16.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
Solution:

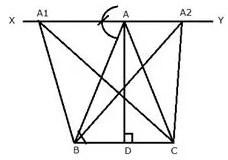
Draw a line XY parallel to the base BC from the vertex A.
This line is the locus of vertex A of all the triangles which have the base BC and length of altitude equal to AD.

Question 17.
In the given figure, obtain all the points equidistant from lines m and n ; and 2.5 cm from O.

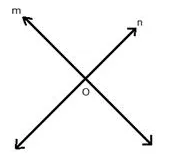
Solution:

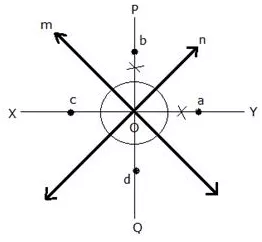
Draw an angle bisector PQ and XY of angles formed by the lines m and n. From O, draw arcs with radius 2.5 cm, which intersect the angle bisectors at a, b, c and d respectively.
Hence, a, b, c and d are the required four points.

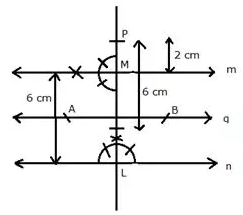
Question PQ.
By actual drawing obtain the points equidistant from lines m and n and 6 cm from the point P, where P is 2 cm above m, m is parallel to n and m is 6 cm above n.
Solution:
Steps of construction:
i) Draw a linen.
ii) Take a point Lonn and draw a perpendicular to n.
iii) Cut off LM = 6 cm and draw a line q, the perpendicular bisector of LM.
iv) At M, draw a line m making an angle of 90°.
v) Produce LM and mark a point P such that PM = 2 cm.
vi) From P, draw an arc with 6 cm radius which intersects the line q, the perpendicular bisector of LM, at A and B.
A and B are the required points which are equidistant from m and n and are at a distance of 6 cm from P.

Question 18.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is:
(i) always 4 cm from the line AB
(ii) equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
Solution:

(i) Draw a line segment AB = 8 cm.
(ii) Draw two parallel lines l and m to AB at a distance of 4 cm.
(iii) Draw the perpendicular bisector of AB which intersects the parallel lines l and m at X and Y respectively then, X and Y are the required points.
(iv) Join AX, AY, BX and BY.
The figure AXBY is a square as its diagonals are equal and intersect at 90°.

Question 19.
Angle ABC = 60° and BA = BC = 8 cm. The mid-points of BA and BC are M and N respec¬tively. Draw and describe the locus of a point which is :
(i) equidistant from BA and BC.
(ii) 4 cm from M.
(iii) 4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
Solution:

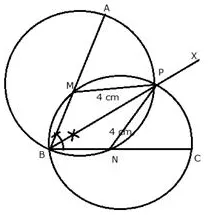
i) Draw an angle of 60° with AB = BC = 8 cm
ii) Draw the angle bisector BX of ∠ABC
iii) With centre M and N, draw circles of radius equal to 4 cm, which intersects each other at P. P is the required point.
iv) Join MP, NP
BMPN is a rhombus since MP = BM = NB = NP = 4 cm

Question 20.
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label:
(i) the locus of the centers of all circles which touch AB and AC.
(ii) the locus of the centers of all circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC.
Solution:

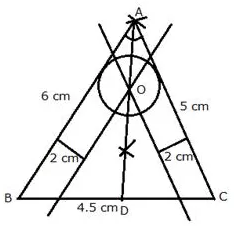
Steps of Construction:
i) Draw a line segment BC = 4.5 cm
ii) With B as centre and radius 6 cm and C as centre and radius 5 cm, draw arcs which intersect each other at A.
iii) Join AB and AC.
ABC is the required triangle.
iv) Draw the angle bisector of ∠BAC
v) Draw lines parallel to AB and AC at a distance of 2 cm, which intersect each other and AD at O.
vi) With centre O and radius 2 cm, draw a circle which touches AB and AC.

Question 21.
Construct a triangle ABC, having given AB = 4.8 cm. AC = 4 cm and ∠ A = 75°. Find a point P.
(i) inside the triangle ABC.
(ii) outside the triangle ABC.
equidistant from B and C; and at a distance of 1.2 cm from BC.
Solution:

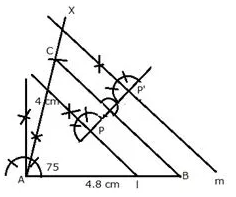
Steps of Construction:
i) Draw a line segment AB = 4.8 cm
ii) At A, draw a ray AX making an angle of 75°
iii) Cut off AC = 4 cm from AX
iv) Join BC.
ABC is the required triangle.
v) Draw two lines l and m parallel to BC at a distance of 1.2 cm
vi) Draw the perpendicular bisector of BC which intersects l and m at P and P’
P and P’ are the required points which are inside and outside the given triangle ABC.

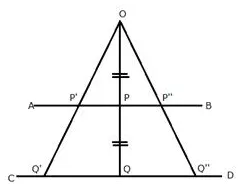
Question PQ.
O is a fixed point. Point P moves along a fixed line AB. Q is a point on OP produced such that OP = PQ. Prove that the locus of point Q is a line parallel to AB.
Solution:
P moves along AB, and Qmoves in such a way that PQ is always equal to OP.
But Pis the mid-point of OQ
Now in ∆OQQ’
P’and P” are the mid-points of OQ’ and OQ”
Therefore, AB||Q’Q”
Therefore, Locus of Q is a line CD which is parallel to AB.

Question 22.
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
Solution:

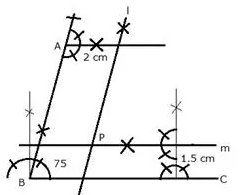
Steps of Construction:
i) Draw a ray BC.
ii) At B, draw a ray BA making an angle of 75° with BC.
iii) Draw a line l parallel to AB at a distance of 2 cm
iv) Draw another line m parallel to BC at a distance of 1.5 cm which intersects line l at P.
P is the required point.

Question 23.
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Solution:

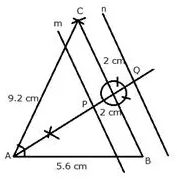
Steps of Construction:
i) Draw a line segment AB = 5.6 cm
ii) From A and B, as centers and radius 9.2 cm, make two arcs which intersect each other at C.
iii) Join CA and CB.
iv) Draw two lines n and m parallel to BC at a distance of 2 cm
v) Draw the angle bisector of ∠BAC which intersects m and n at P and Q respectively.
P and Q are the required points which are equidistant from AB and AC.
On measuring the distance between P and Q is 4.3 cm.

Question 24.
Construct a triangle ABC, with AB = 6 cm, AC = BC = 9 cm. Find a point 4 cm from A and equidistant from B and C.
Solution:

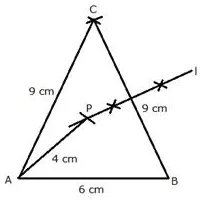
Steps of Construction:
i) Draw a line segment AB = 6 cm
ii) With A and B as centers and radius 9 cm, draw two arcs which intersect each other at C.
iii) Join AC and BC.
iv) Draw the perpendicular bisector of BC.
v) With A as centre and radius 4 cm, draw an arc which intersects the perpendicular bisector of BC at P.
P is the required point which is equidistant from B and C and at a distance of 4 cm from A.

Question 25.
Ruler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.
(i) Construct a triangle ABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.
(ii) Construct the locus of all points inside triangle ABC, which are equidistant from B and C.
(iii) Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.
(iv) Mark the point Q, in your construction, which would make A QBC equal in area to A ABC, and isosceles.
(v) Measure and record the length of CQ.
Solution:

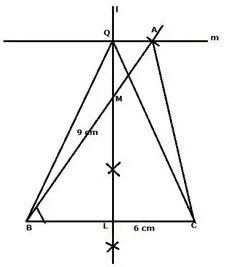
Steps of Construction:
(i) Draw a line segment BC = 6 cm.
(ii) At B, draw a ray BX making an angle 60 degree and cut off BA=9 cm.
(iii) Join AC. ABC is the required triangle.
(iv) Draw perpendicular bisector of BC which intersects BA in M, then any point on LM is equidistant from B and C.
(v) Through A, draw a line m || BC.
(vi) The perpendicular bisector of BC and the parallel line m intersect each other at Q.
(vii) Then triangle QBC is equal in area to triangle ABC. m is the locus of all points through which any triangle with base BC will be equal in area of triangle ABC.
On measuring CQ = 8.4 cm.

Question 26.
State the locus of a point in a rhombus ABCD, which is equidistant
(i) from AB and AD;
(ii) from the vertices A and C.
Solution:

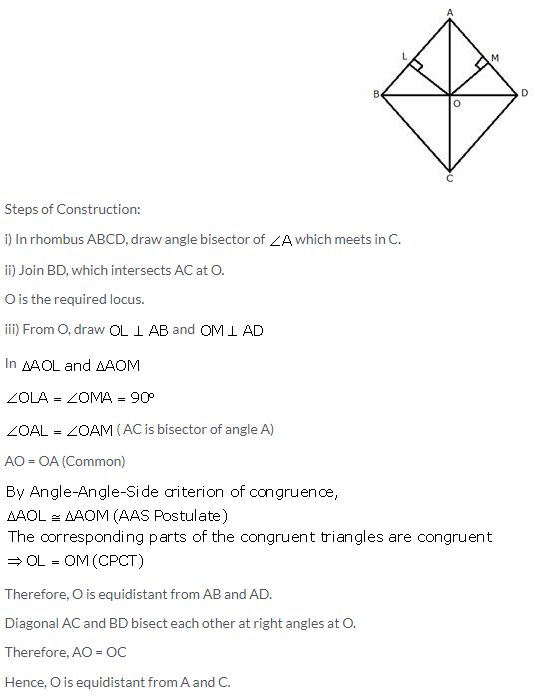
Question 27.
Use a graph paper for this question. Take 2 cm = 1 unit on both the axes.
(i) Plot the points A(1,1), B(5,3) and C(2,7).
(ii) Construct the locus of points equidistant from A and B.
(iii) Construct the locus of points equidistant from AB and AC.
(iv) Locate the point P such that PA = PB and P is equidistant from AB and AC.
(v) Measure and record the length PA in cm.
Solution:

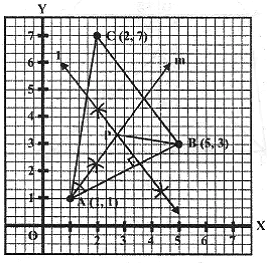
Steps of Construction:
i) Plot the points A(1, 1), B(5, 3) and C(2, 7) on the graph and join AB, BC and CA.
ii) Draw the perpendicular bisector of AB and angle bisector of angle A which intersect each other at P.
P is the required point.
Since P lies on the perpendicular bisector of AB.
Therefore, P is equidistant from A and B.
Again,
Since P lies on the angle bisector of angle A.
Therefore, P is equidistant from AB and AC.
On measuring, the length of PA = 5.2 cm

Question 28.
Construct an isosceles triangle ABC such that AB = 6 cm, BC=AC=4cm. Bisect angle C internally and mark a point P on this bisector such that CP = 5cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Solution:

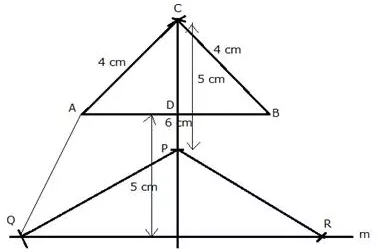
Steps of Construction:
i) Draw a line segment AB = 6 cm.
ii) With centers A and B and radius 4 cm, draw two arcs which intersect each other at C.
iii) Join CA and CB.
iv) Draw the angle bisector of angle C and cut off CP = 5 cm.
v) A line m is drawn parallel to AB at a distance of 5 cm.
vi) P as centre and radius 5 cm, draw arcs which intersect the line m at Q and R.
vii) Join PQ, PR and AQ.
Q and R are the required points.

Question PQ.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of lengths 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.
Solution:

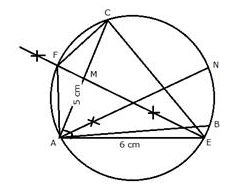
Steps of Construction:
i) Draw a circle with radius = 4 cm.
ii) Take a point A on it.
iii) A as centre and radius 6 cm, draw an arc which intersects the circle at B.
iv) Again A as centre and radius 5 cm, draw an arc which intersects the circle at C.
v) Join AB and AC.
vi) Draw the perpendicular bisector of AC, which intersects AC at Mand meets the circle at E and F.
EF is the locus of points inside the circle which are equidistant from A and C.
vii) Join AE, AF, CE and CF.
Proof:

Similarly, we can prove that CF = AF
Hence EF is the locus of points which are equidistant from A and C.
ii) Draw the bisector of angle A which meets the circle at N.
Therefore. Locus of points inside the circle which are equidistant from AB and AC is the perpendicular bisector of angle A.

Question 29.
Plot the points A(2,9), B(-1,3) and C(6,3) on a graph paper. On the same graph paper, draw the locus of point A so that the area of triangle ABC remains the same as A moves.
Solution:

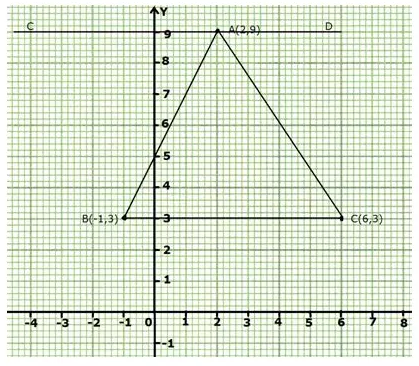
Steps of construction:
i) Plot the given points on graph paper.
ii) Join AB, BC and AC.
iii) Draw a line parallel to BC at A and mark it as CD.
CD is the required locus of point A where area of triangle ABC remains same on moving point A.

Question 30.
Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
(i) Complete the rectangle ABCD such that:
(a) P is equidistant from A B and BC.
(b) P is equidistant from C and D.
(ii) Measure and record the length of AB.
Solution:

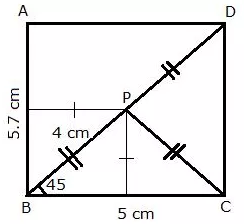
i) Steps of Construction:
1) Draw a line segment BC = 5 cm
2) B as centre and radius 4 cm draw an arc at an angle of 45 degrees from BC.
3) Join PC.
4) B and C as centers, draw two perpendiculars to BC.
5) P as centre and radius PC, cut an arc on the perpendicular on C at D.
6) D as centre, draw a line parallel to BC which intersects the perpendicular on B at A.
ABCD is the required rectangle such that P is equidistant from AB and BC (since BD is angle bisector of angle B) as well as C and D.
ii) On measuring AB = 5.7 cm

Question 31.
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown.
(i) Construct a ∆ABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.
(ii) Construct the locus of points at a distance of 3.5 cm from A.
(iii) Construct the locus of points equidistant from AC and BC.
(iv) Mark 2 points X and Y which are at distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
Solution:
i. Steps of construction:

1. Draw BC = 6.5 cm using a ruler.
2. With B as center and radius equal to approximately half of BC, draw an arc that cuts the segment BC at Q.
3. With Q as center and same radius, cut the previous arc at P.
4. Join BP and extend it.
5. With B as center and radius 5 cm, draw an arc that cuts the arm PB to obtain point A.
6. Join AC to obtain ΔABC.

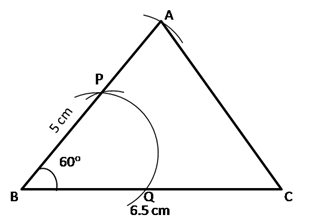
ii. With A as center and radius 3.5 cm, draw a circle.
The circumference of a circle is the required locus.

iii. Draw CH, which is bisector of Δ ACB. CH is the required locus.

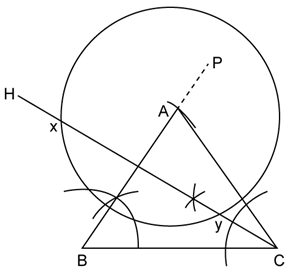
iv. Circle with center A and line CH meet at points X and Y as shown in the figure. xy = 8.2 cm (approximately)

More Resources for Selina Concise Class 10 ICSE Solutions

• Selina Maths Class 10 ICSE Solutions
• Selina ICSE Physics Class 10 Solutions
• Concise Chemistry Class 10 ICSE Guide Pdf
• Selina ICSE Class 10 Biology Solutions

ICSE Solutions Selina ICSE Solutions