Selina Concise Mathematics Class 10 ICSE Solutions Chapterwise Revision Exercises

Selina Concise Mathematics Class 10 ICSE Solutions Chapterwise Revision Exercises

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapterwise Revision Exercises.

Sales-Tax (VAT)

Question 1.
A man purchased a pair of shoes for ₹809.60 which includes 8% rebate on the marked price and then 10% sales tax on the remaining price. Find the marked price of the pair of shoes.
Solution:

Question 2.
The catalogue price of an article is ₹36,000. The shopkeeper gives two successive discounts of 10% each. He further gives an off-season discount of 5 % on the balance. If sales-tax at the rate 10% is charged on the remaining amount, find :
(i) the sales tax charged
(ii) the selling price of the article including sales-tax.
Solution:

Question 3.
A sells an article to B for ₹80,000 and charges sales-tax at 8%. B sells the same article to C for ₹1,12,000 and charges sales- tax at the rate of 12%. Find the VAT paid by B in this transaction.
Solution:

Question 4.
The marked price of an article is ₹1,600. Mohan buys this article at 20% discount and sells it at its marked price. If the sales-tax at each stage is 6%; find :
(i) the price at which the article can be bought,
(ii) the VAT (value added tax) paid by Mohan.
Solution:

Question 5.
A sells an old laptop to B for ₹12,600; B sells it to C for ₹14,000 and C sells the same laptop to D for ₹16,000.
If the rate of VAT at each stage is 10%, find the VAT paid by :
(i) B
(ii) C
Solution:

Banking

Question 6.
Ashok deposits ₹3200 per month in a cumulative account for 3 years at the rate of 9% per annum. Find the maturity value of this account
Solution:

Question 7.
Mrs. Kama has a recurring deposit account in Punjab National Bank for 3 years at 8% p.a. If she gets ₹9,990 as interest at the time of maturity, find:
(i) the monthly instalment.
(ii) the maturity value of the account.
Solution:

Question 8.
A man has a 5 year recurring deposit account in a bank and deposits ₹240 per month. If he receives ₹17,694 at the time of maturity, find the rate of interest.
Solution:

Question 9.
Sheela has a recurring deposit account in a bank of ₹2,000 per month at the rate of 10% per anum. If she gets ₹83,100 at the time of maturity, find the total time (in years) for which the account was held.
Solution:

Question 10.
A man deposits ₹900 per month in a recurring account for 2 years. If he gets 1,800 as interest at the time of maturity, find the rate of interest .
Solution:

Shares And Dividend

Question 11.
What is the market value of 4 \(\frac { 1 }{ 2 }\) % (₹100) share, when an investment of ₹1,800 produces an income of ₹72 ?
Solution:

Question 12.
By investing ₹10,000 in the shares of a company, a man gets an income of ₹800; the dividend being 10%. If the face-value of each share is ₹100, find :
(i) the market value of each share.
(ii) the rate per cent which the person earns on his investment.
Solution:

Question 13.
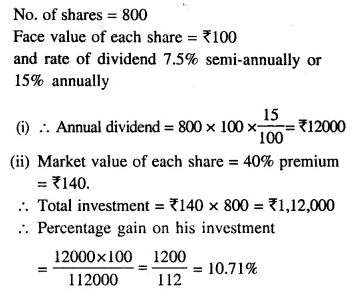
A man holds 800 shares of ₹100 each of a company paying 7.5% dividend semiannually.
(i) Calculate his annual dividend.
(ii) If he had bought these shares at 40% premium, what percentage return does he get on his investment ?
Solution:

Question 14.
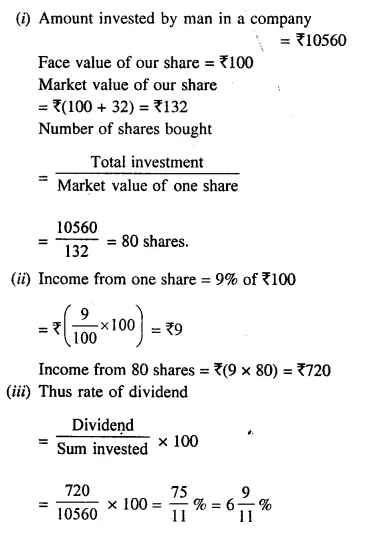
A man invests ₹10,560 in a company, paying 9% dividend, at the time when its ₹100 shares can be bought at a premium of ₹32. Find:
(i) the number of shares bought by him;
(ii) his annual income from these shares and
(iii) the rate of return on his investment .
Solution:

Question 15.
Find the market value of 12% ₹25 shares of a company which pays a dividend of ₹1,875 on an investment of ₹20,000.
Solution:

Linear Inequations

Question 16.
The given diagram represents two sets A and B on real number lines.

(i) Write down A and B in set builder notation.
(ii) Represent A ∪ B, A ∩ B, A’ ∩ B, A – B and B – A on separate number lines.
Solution:

Question 17.
Find the value of x, which satisfy the inequation:

Graph the solution set on the real number line .
Solution:

Question 18.
State for each of the following statements whether it is true or false :
(a) If (x – a) (x – b) < 0, then x < a, and x < b.
(b) If a < 0 and b < 0, then (a + b)² > 0.
(c) If a and b are any two integers such that a > b, then a² > b².
(d) If p = q + 2, then p > q.
(e) If a and b are two negative integers such that a < b , then \(\frac { 1 }{ a }\) < \(\frac { 1 }{ b }\)
Solution:

Question 19.
Given 20 – 5x < 5(x + 8), find the smallest value of x when :
(i) x \(\epsilon\) I
(ii) x \(\epsilon\) W
(iii) x \(\epsilon\) N
Solution:

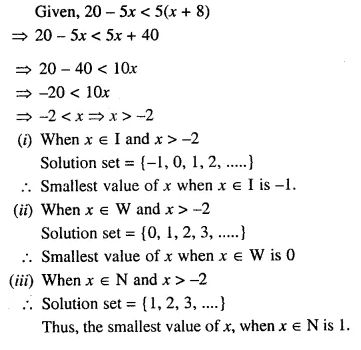
Question 20.
If x \(\epsilon\) Z, solve : 2 + 4x < 2x – 5 < 3x. Also, represent its solution on the real number line.
Solution:

Quadratic Equation

Question 21.

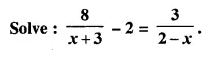
Solution:

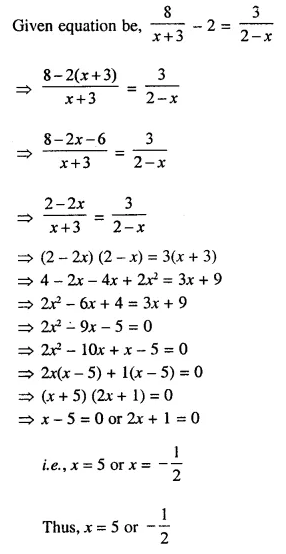
Question 22.

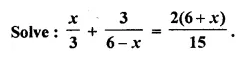
Solution:

Question 23.
Find the value of k for which the roots of the following equation are real and equal k²x² – 2 (2k -1) x + 4 = 0
Solution:

Question 24.

Solution:

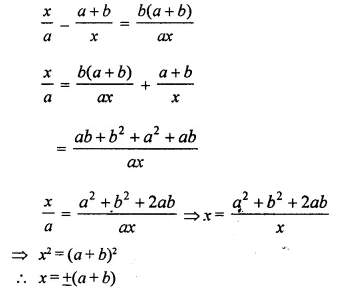
Question 25.
If -5 is a root of the quadratic equation 2x² +px -15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, find the value of k.
Solution:

Problems On Quadratic Equations

Question 26.
x articles are bought at ₹(x – 8) each and (x – 2) some other articles are bought at ₹(x – 3) each. If the total cost of all these articles is ₹76, how many articles of first kind were bought ?
Solution:

Question 27.
In a two digit number, the unit’s digit exceeds its ten’s digit by 2. The product of the given number and the sum of its digits is equal to 144. Find the number.
Solution:

Question 28.
The time taken by a person to cover 150 km was 2.5 hours more than the time taken in return journey. If he returned at a speed of 10 km/hour more than the speed of going, what was the speed per hour in each direction ?
Solution:

Question 29.
A takes 9 days more than B to do a certain piece of work. Together they can do the work in 6 days. How many days will A alone take to do the work ?
Solution:

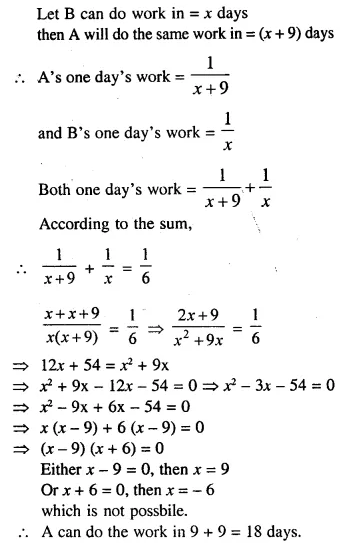
Question 30.
A man bought a certain number of chairs for ₹10,000. He kept one for his own use and sold the rest at the rate ₹50 more than he gave for one chair. Besides getting his own chair for nothing, he made a profit of ₹450. How many chairs did he buy ?
Solution:

Question 31.
In the given figure; the area of unshaded portion is 75% of the area of the shaded portion. Find the value of x.

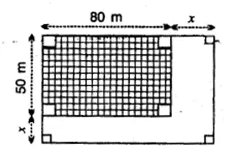
Solution:

Ratio And Proportion

Question 32.

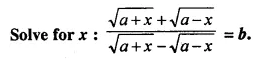
Solution:

Question 33.
If a:b = 2:3,b:c = 4:5 and c: d = 6:7, find :a:b :c :d.
Solution:

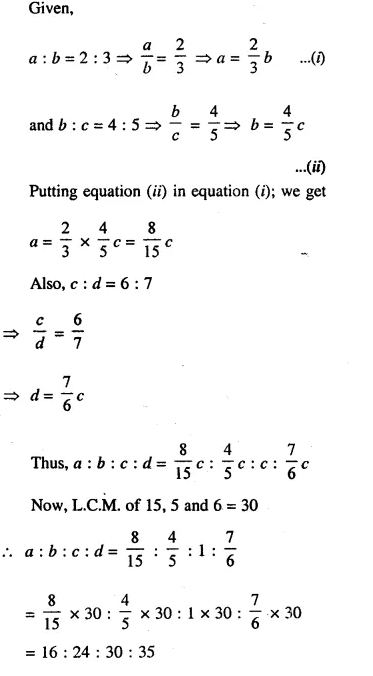
Question 34.

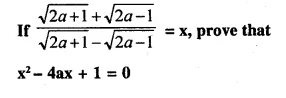
Solution:

Question 35.
Find the compound ratio of:
(i) (a-b) : (a+b) and (b²+ab): (a²-ab)
(ii) (x+y): (x-y); (x²+y²): (x+y)² and (x²-y²)²: (x⁴-y⁴)
(iii) (x²– 25): (x²+ 3x – 10); (x²-4): (x²+ 3x+2) and (x + 1): (x² + 2x)
Solution:

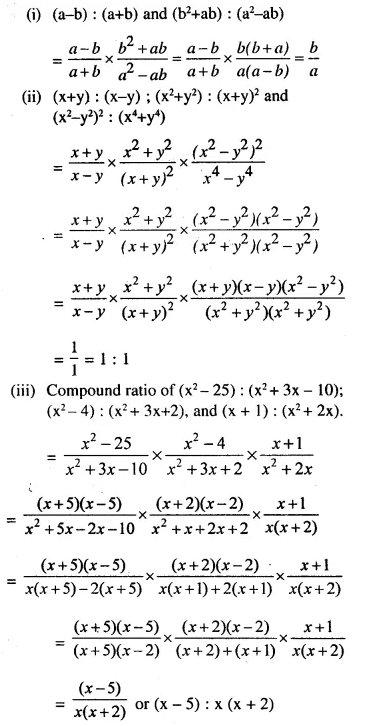
Question 36.
The ratio of the prices of two fans was 16: 23. Two years later, when the price of the first fan had risen by 10% and that of the second by Rs. 477, the ratio of their prices became 11: 20. Find the original prices of two fans.
Solution:
The ratio of prices of two fans = 16 : 23
Let the price of first fan = 6x
then price of second fan = 23x

Remainder And Factor Theorems

Question 37.
Given that x + 2 and x – 3 are the factors of x³ + ax + b, calculate the values of a and b. Also find the remaining factor.
Solution:

Question 38.
Use the remainder theorem to factorise the expression 2x³ + 9x² + 7x – 6 = 0 Hense, solve the equation 2x³ + 9x² + 7 x – 6 = 0
Solution:

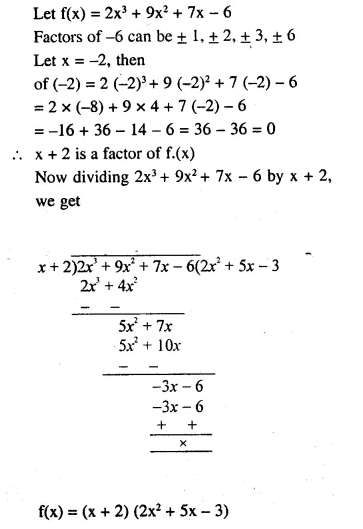
Question 39.
When 2x³ + 5x² – 2x + 8 is divided by (x – a) the remainder is 2a³ + 5a². Find the value of a.
Solution:

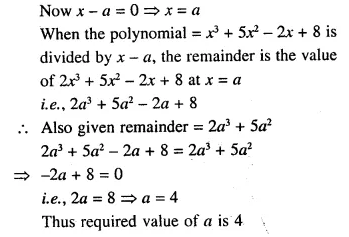
Question 40.
What number should be added to x³ – 9x² – 2x + 3 so that the remainder may be 5 when divided by (x – 2) ?
Solution:

Question 41.
Let R₁ and R₂ are remainders when the polynomials x³ + 2x² – 5ax – 7 and x³ + ax² – 12x + 6 are divided by (x +1) and (x – 2) respectively. If 2R₁ + R₂ = 6; find the value of a.
Solution:

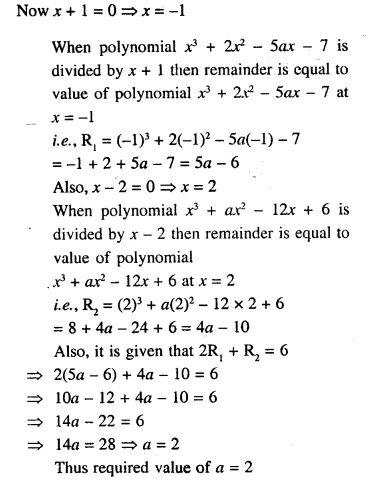
Matrices

Question 42.

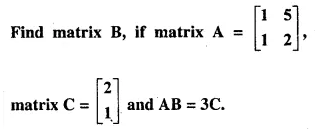
Solution:

Question 43.

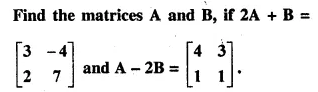
Solution:

Question 44.

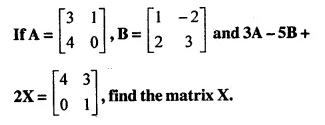
Solution:

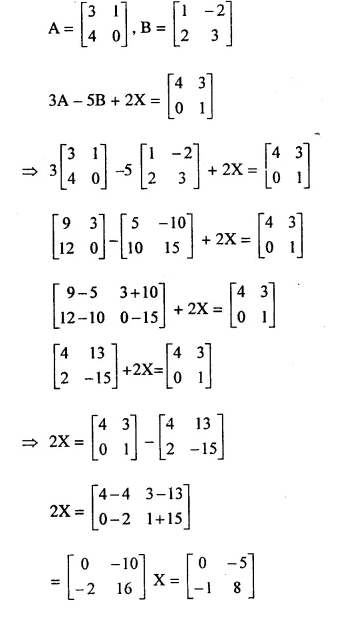
Question 45.

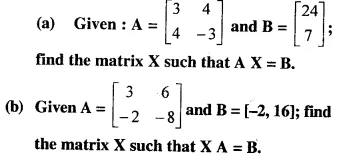
Solution:

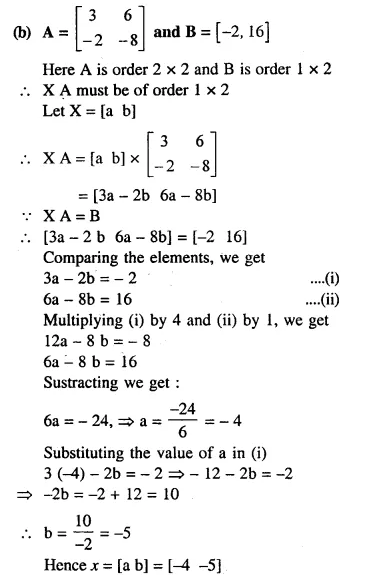
Arithmetic Progression (A.P.)

Question 46.
Find the 15th term of the A.P. with second term 11 and common difference 9.
Solution:

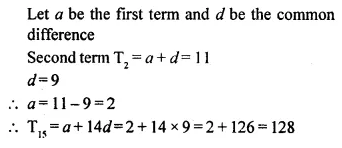
Question 47.
How many three digit numbers are divisible by 7 ?
Solution:

Question 48.
Find the sum of terms of the A.P.: 4,9,14,…….,89.
Solution:

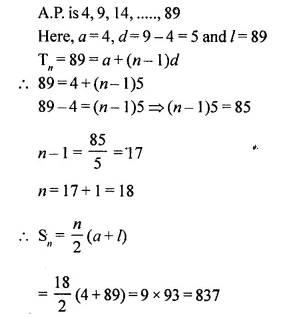
Question 49.
Daya gets pocket money from his father every day. Out of the pocket money, he saves ₹2.75 on first day, ₹3.00 on second day, ₹3.25 on third day and so on. Find:
(i) the amount saved by Daya on 14th day.
(ii) the amount saved by Daya on 30th day.
(iii) the total amount saved by him in 30 days.
Solution:

Question 50.
If the sum of first m terms of an A.P. is n and sum of first n terms of the same A.P. is m. Show that sum of first (m + n) terms of it is (m + n).
Solution:

Geometric Progression (GP.)

Question 51.
3^rd term of a GP. is 27 and its 6th term is 729; find the product of its first and 7^th terms.
Solution:

Question 52.
Find 5 geometric means between 1 and 27.
Solution:

Question 53.
Find the sum of the sequence 96 – 48 + 24…. upto 10 terms.
Solution:

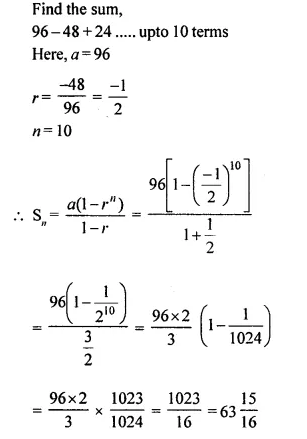
Question 54.
Find the sum of first n terms of:
(i) 4 + 44 + 444 + …….
(ii) 0.7 + 0.77 + 0.777 + …..
Solution:

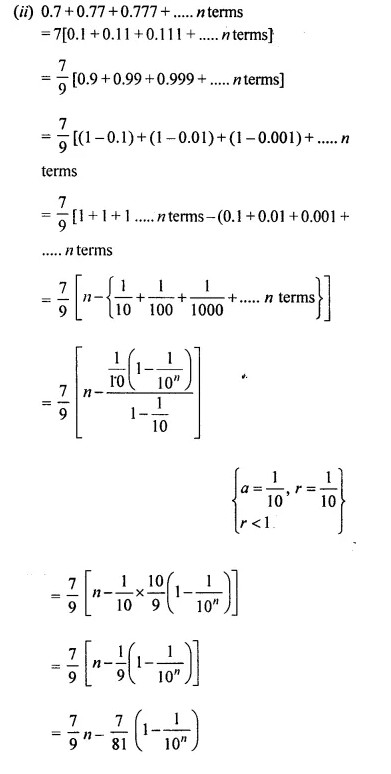
Question 55.
Find the value of 0.4\(\mathring { 2 } \)\(\mathring { 3 } \).
Solution:

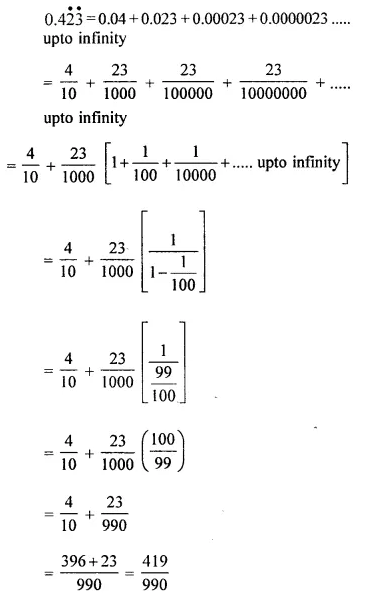
Reflection

Question 56.
Find the values of m and n in each case if:
(i) (4, -3) on reflection in x-axis gives (-m, n)
(ii) (m, 5) on reflection in y-axis gives (-5, n-2)
(iii) (-6, n+2) on reflection in origin gives (m+3, -4)
Solution:

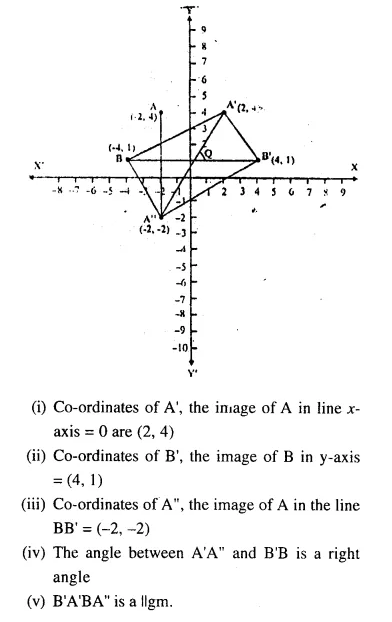
Question 57.
Points A and B have the co-ordinates (-2,4) and (-4,1) respectively. Find :
(i) The co-ordinates of A’, the image of A in the line x = 0.
(ii) The co-ordinates of B’, the image of Bin y-axis.
(iii) The co-ordinates of A”, the image of A in the line BB’,
Hence, write the angle between, the lines A’A” and B B’. Assign a special name to the figure B’ A’ B A”
Solution:

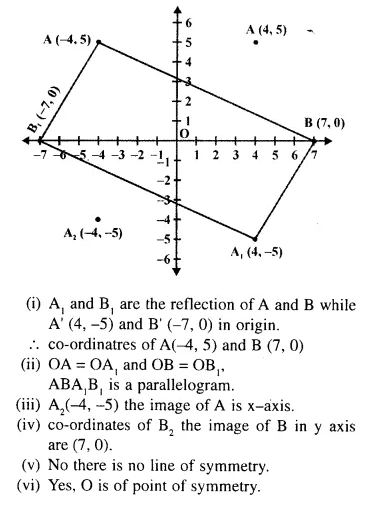
Question 58.
Triangle OA₁B₁ is the reflection of triangle OAB in origin, where A, (4, -5) is the image of A and B, (-7, 0) is the image of B.
(i) Write down the co-ordinates of A and B and draw a diagram to represent this information.
(ii) Give the special name to the quadrilateral ABA₁ B₁. Give reason.
(iii) Find the co-ordinates of A₂, the image of A under reflection in x-axis followed by reflection in y-axis.
(iv) Find the co-ordinates of B₂, the image of B under reflection in y-axis followed by reflection in origin.
(v) Does the quadrilateral obtained has any line symmetry ? Give reason.
(vi) Does it have any point symmetry ?
Solution:

Section And Mid-Point Formulae

Question 59.
In what ratio does the point M (P, -1) divide the line segment joining the points A (1,-3) and B (6,2) ? Hence, find the value of p.
Solution:

Question 60.
A (-4,4), B (x, -1) and C (6,y) are the vertices of ∆ABC. If the centroid of this triangle ABC is at the origin, find the values of x and y.
Solution:

Question 61.
A (2,5), B (-1,2) and C (5,8) are the vertices of a triangle ABC. Pand Q are points on AB and AC respectively such that AP: PB=AQ: QC = 1:2.
(a) Find the co-ordinates of points P and Q
(b) Show that BC = 3 x PQ.
Solution:

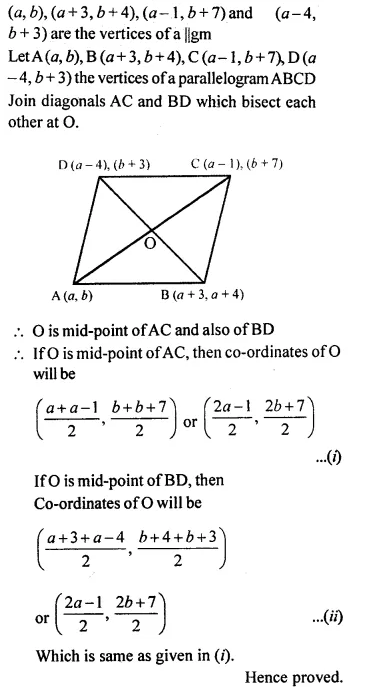
Question 62.
Show that the points (a, b), (a+3, b+4), (a -1, b + 7) and (a – 4, b + 3) are the vertices of a parallelogram.
Solution:

Equation Of straight Line

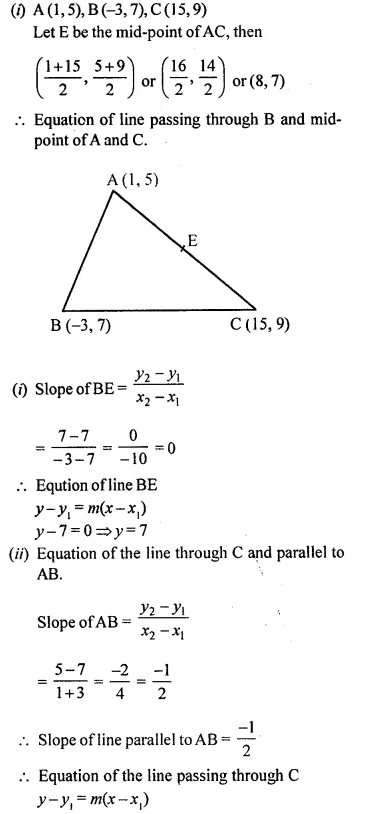
Question 63.
Given points A(l, 5), B (-3,7) and C (15,9).
(i) Find the equation of a line passing through the mid-point of AC and the point B.
(ii) Find the equation of the line through C and parallel to AB.
(iii) The lines obtained in parts (i) and (ii) above, intersect each other at a point P. Find the co-ordinates of the point P.
(iv) Assign, giving reason, a special names of the figure PABC.
Solution:

Question 64.
The line x- 4y=6 is the perpendicular bisector of the line segment AB. If B = (1,3); find the co-ordinates of point A.
Solution:

Question 65.
Find the equation of a line passing through the points (7, -3) and (2, -2). If this line meets x- axis at point P and y-axis at point Q; find the co-ordinates of points P and Q.
Solution:

Question 66.
A (-3,1), B (4,4) and C (1, -2) are the vertices of a triangle ABC. Find:
(i) the equation of median BD,
(ii) the equation of altitude AE.
Solution:

Question 67.
Find the equation of perpendicular bisector of the line segment joining the points (4, -3) and (3,1).
Solution:

Question 68.
(a) If (p +1) x + y = 3 and 3y – (p -1) x = 4 are perpendicular to each other find the value of p.
(b) If y + (2p +1) x + 3 = 0 and 8y – (2p -1) x = 5 are mutually prependicular, find the value of p.
Solution:

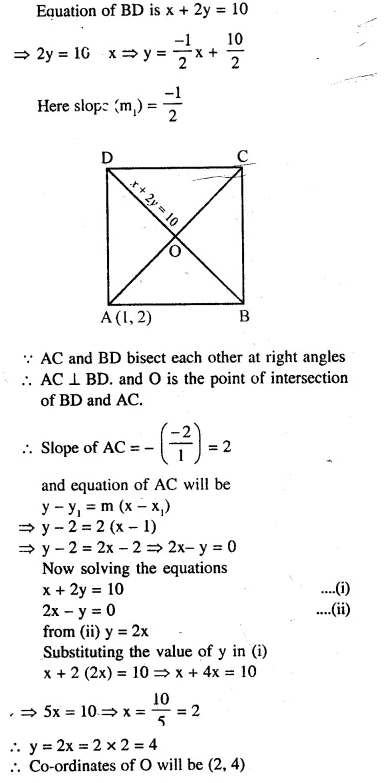
Question 69.
The co-ordinates of the vertex A of a square ABCD are (1, 2) and the equation of the diagonal BD is x + 2y = 10. Find the equation of the other diagonal and the coordinates of the centre of the square.
Solution:

Similarity

Question 70.
M is mid-point of a line segment AB; AXB and MYB are equilateral triangles on opposite sides of AB; XY cuts AB at Z. Prove that AZ = 2ZB.
Solution:

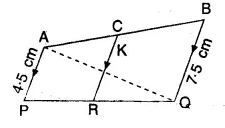
Question 71.
In the given figure, if AC = 3cm and CB = 6 cm, find the length of CR.

Solution:

Question 72.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO : OD = 4:7; find:
(i) ∆AOD : ∆AOB
(ii) ∆AOB : ∆ACB
(iii) ∆DOC : ∆AOB
(iv) ∆ABD : ∆BOC
Solution:

Question 73.
A model of a ship is made to a scale of 1 : 160. Find :
(i) the length of the ship, if the length of its model is 1.2 m.
(ii) the area of the deck of the ship, if the area of the deck of its model is 1.2 m².
(iii) the volume of the ship, if the volume of its model is 1.2m³.
Solution:

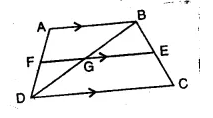
Question 74.
In trapezium ABCD, AB || DC and DC = 2 AB. EF, drawn parallel to AB cuts AD in F and BC in E such that 4 BE = 3 EC. Diagonal DB intersects FE at point G Prove that: 7 EF = 10 AB.

Solution:

Loci

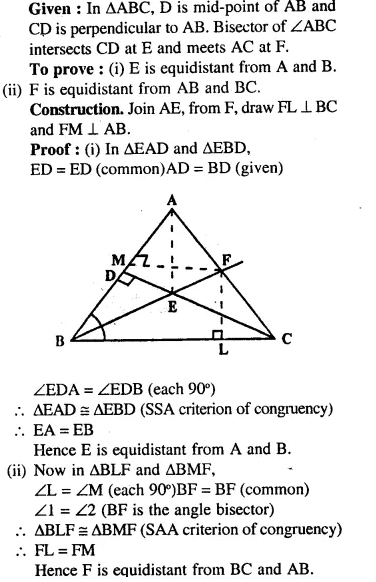
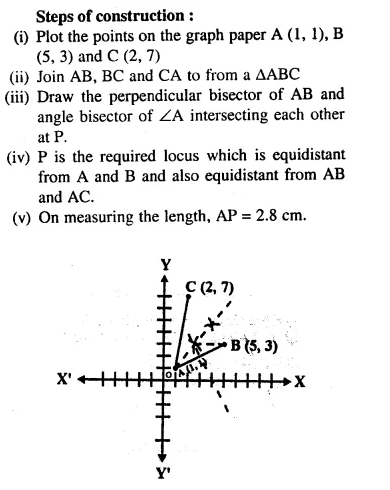
Question 75.
In triangle ABC, D is mid-point of AB and CD is perpendicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
(i) E is equidistant from A and B.
(ii) F is equidistant from AB and BC.
Solution:

Question 76.
Use graph paper for this questions. Take 2 cm = 1 unit on both axes.
(i) Plot the points A (1,1), B (5,3) and C (2,7)
(ii) Construct the locus of points equidistant from A and B.
(iii) Construct the locus of points equidistant from AB and AC.
(iv) Locate the point P such that PA = PB and P is equidistant from AB and AC.
(v) Measure and record the length PA in cm.
Solution:

Circles

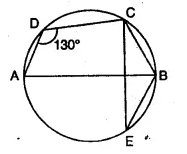
Question 77.
In the given figure, ∠ADC = 130° and BC = BE. Find ∠CBE if AB ⊥ CE.

Solution:

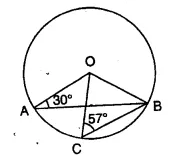
Question 78.
In the given figure, ∠OAB=30° and ∠OCB= 57°, find ∠BOC and ∠AOC.

Solution:

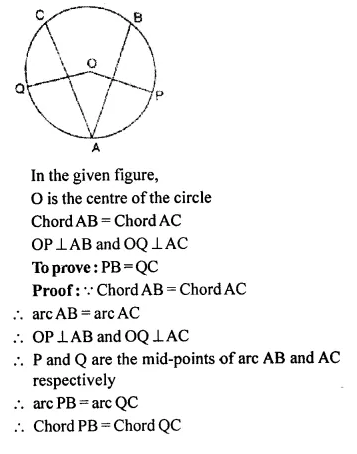
Question 79.
In the given figure, O is the centre of the circle. If chord AB = chord AC, OP⊥ AB and OQ⊥ AC; show that: PB=QC.
Solution:

Question 80.
In the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30°, find:
(i) ∠AOX
(ii) ∠APY
(iii) ∠BPY
(iv) ∠OAX

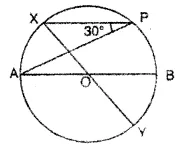
Solution:

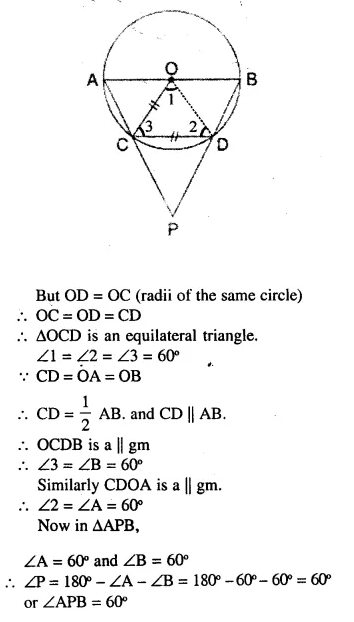
Question 81.
(a) In the adjoining figure; AB = AD, BD = CD and ∠DBC = 2 ∠ABD.
Prove that: ABCD is a cyclic quadrilateral.

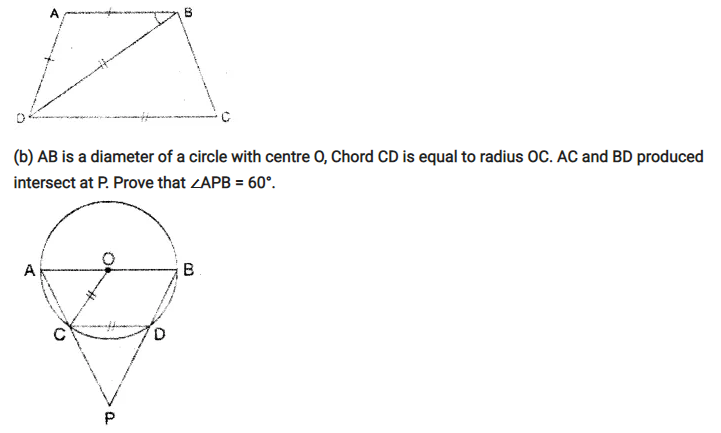
(b) AB is a diameter of a circle with centre O, Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that ∠APB = 60°.

Solution:

Tangents And Intersecting Chords

Question 82.
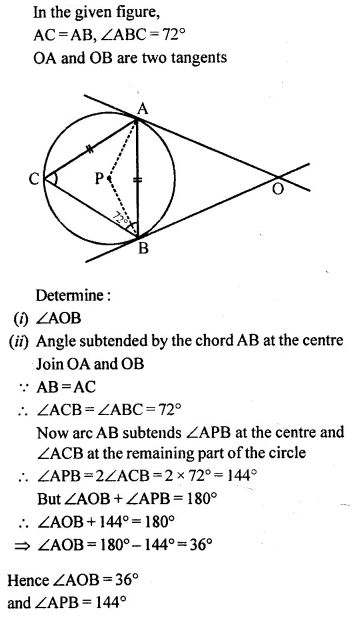
In the given figure, AC=AB and ∠ABC=72°.
OA and OB are two tangents. Determine:
(i) ∠AOB
(ii) angle subtended by the chord AB at the centre.

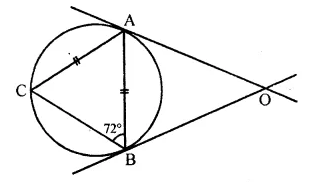
Solution:

Question 83.
In the given figure, PQ, PR and ST are tangents to the same circle. If ∠P = 40° and ∠QRT = 75°, find a, b and c.

Solution:

Question 84.
In the given figure, ∠ABC = 90° and BC is diameter of the given circle. Show that:
(i) AC x AD =AB²
(ii) AC x CD = BC²

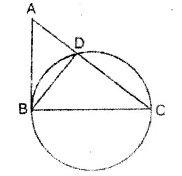
Solution:

Question 85.
In the given figure; AB, BC and CA are tangents to the given circle. If AB = 12 cm, BC = 8 cm and AC=10 cm, find the lengths of AD,BE = CF.

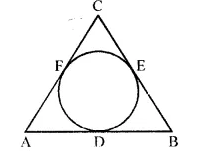
Solution:

Question 86.
(a) AB and CD are two chords of a circle intersecting at a point P inside the circle. If:
(i) AB = 24 cm, AP = 4 cm and PD = 8 cm, determine CP.
(ii) AP = 3 cm, PB = 2.5 cm and CD = 6.5 cm determine CP.
(b) AB and CD are two chords of a circle intersecting at a point P outside the circle. If:
(i) PA = 8 cm, PC – 5 cm and PD = 4 cm, determine AB.
(ii) PC = 30 cm, CD = 14 cm and PA = 24 cm, determine AB.
Solution:

Construction

Question 87.
Construct a triangle ABC in which AC = 5 cm, BC = 7 cm and AB = 6 cm.
(i) Mark D, the mid point of AB.
(ii) Construct a circle which touches BC at C and passes through D.
Solution:

Question 88.
Using ruler and compasses only, draw a circle of radius 4 cm. Produce AB, a diameter of this circle up to point X so that BX = 4cm. Construct a circle to touch AB at X and to touch the circle, drawn earlier externally.
Solution:

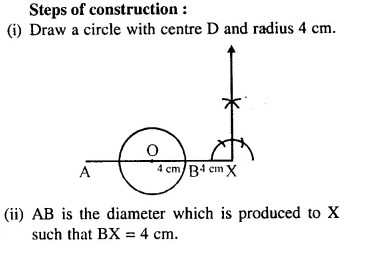
Mensuration

Question 89.
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
Solution:

Question 90.
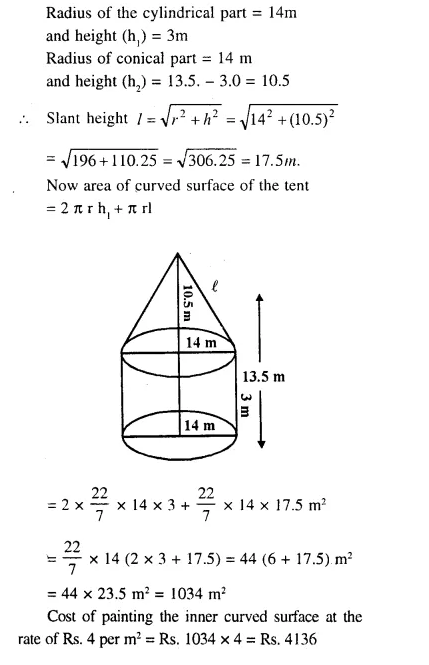
A tent is of the shape of right circular cylinder upto height of 3 metres and then becomes a right circular cone with a maximum height of 13.5 metres above the ground. Calculate the cost of painting the inner surface of the tent at Rs. 4 per sq. metre, if the radius of the base is 14 metres.
Solution:

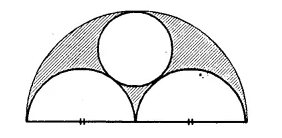
Question P.Q.
In the given figure, diameter of the biggest semi-circle is 108cm, and diameter of the smallest circle is 36 cm. Calculate the area of the shaded portion.

Solution:

Question 91.
A copper wire of diameter 6 mm is evenly wrapped on the cylinder of length 18 cm and diameter 49 cm to cover the whole surface. Find:
(i) the length
(ii) the volume of the wire
Solution:

Question 92.
A pool has a uniform circular cross-section of radius 5 m and uniform depth 1.4m. It is filled by a pipe which delivers water at the rate of 20 litres per sec. Calculate, in minutes, the time taken to All the pool. If the pool is emptied in 42 min. by another cylindrical pipe through which water flows at 2 m per sec, calculate the radius of the pipe in cm.
Solution:

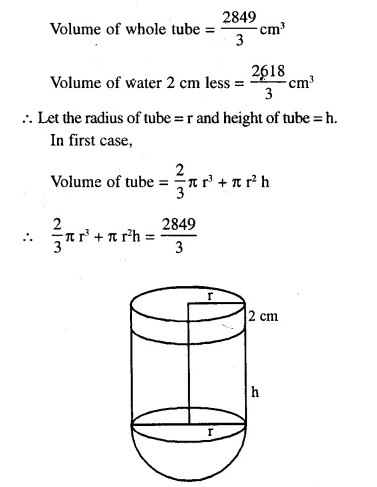
Question 93.
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of water required to fill the whole tube is 2849/3cm³ and 2618/3cm³ of water are required to fill the tube to a level which is 2 cm below the top of the tube. Find the radius of the tube and the length of its cylinderical part.
Solution:

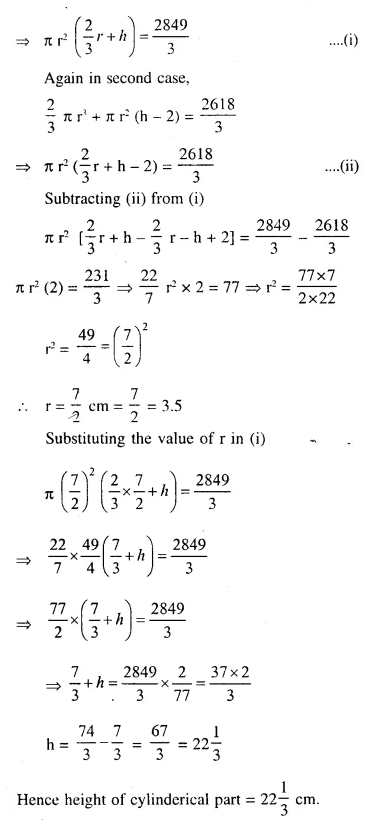
Question 94.
A sphere is placed in an inverted hollow conical vessel of base radius 5 cm and vertical height 12 cm. If the highest point of the sphere is at the level of the base of the cone, find the radius of the sphere. Show that the volume of the sphere and the conical vessel are as 40 : 81.
Solution:

Question 95.
The difference between the outer and the inner curved surface areas of a hollow cylinder, 14cm. long is 88sq. cm. Find the outer and the inner radii of the cylinder given that the volume of metal used is 176 cu. cm.
Solution:

Trigonometry

Question 96.

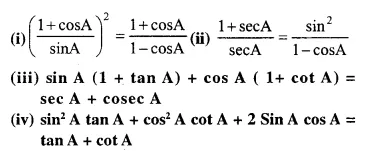
Solution:

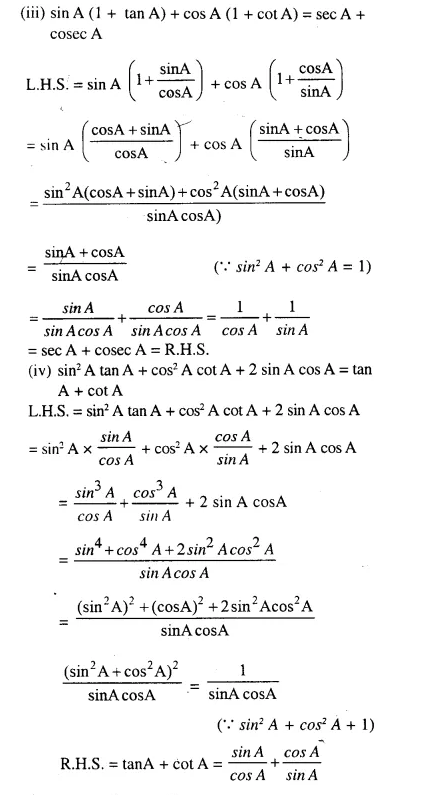
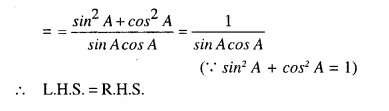
Question 97.
If tan A = 1 and tan B = √3 ; evaluate :
(i) cos A cos B – sin A sin B
(ii) sin A cos B + cos A sin B
Solution:

Question 98.
As observed from the top of a 100 m high light house, the angles, of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
Solution:

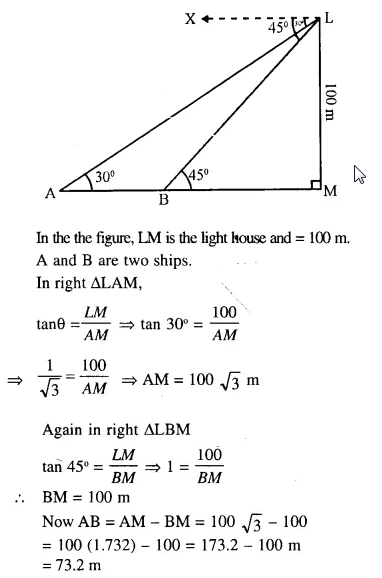
Question 99.

Solution:

Question 100.
From the top of a light house, it is observed that a ship is sailing directly towards it and the angle of depression of the ship changes from 30° to 45° in 10 minutes. Assuming that the ship is sailing with uniform speed; calculate in how much more time (in minutes) will the ship reach to the light house.
Solution:
Let LM be the height of light house = h
Angle of depression changes from 30° to 45° in 10 minutes.

Statistics 

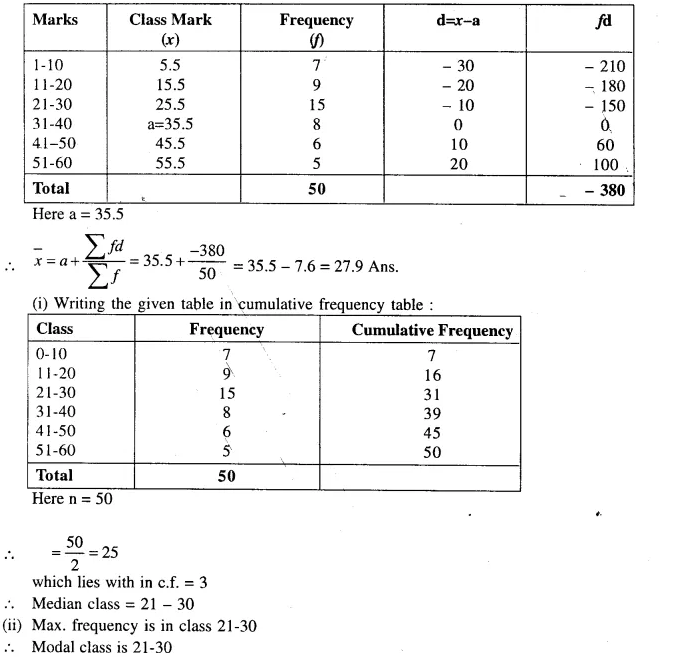
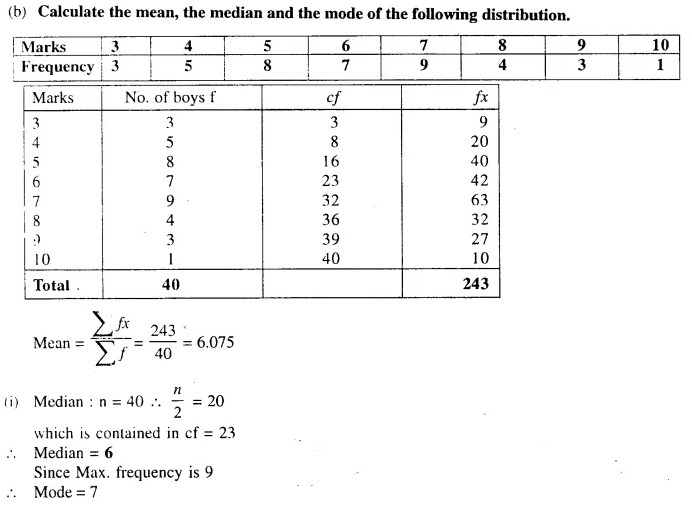
Question 101.
Calculate the mean mark in the distribution given below :

Also state (i) median class (ii) the modal class.
Solution:

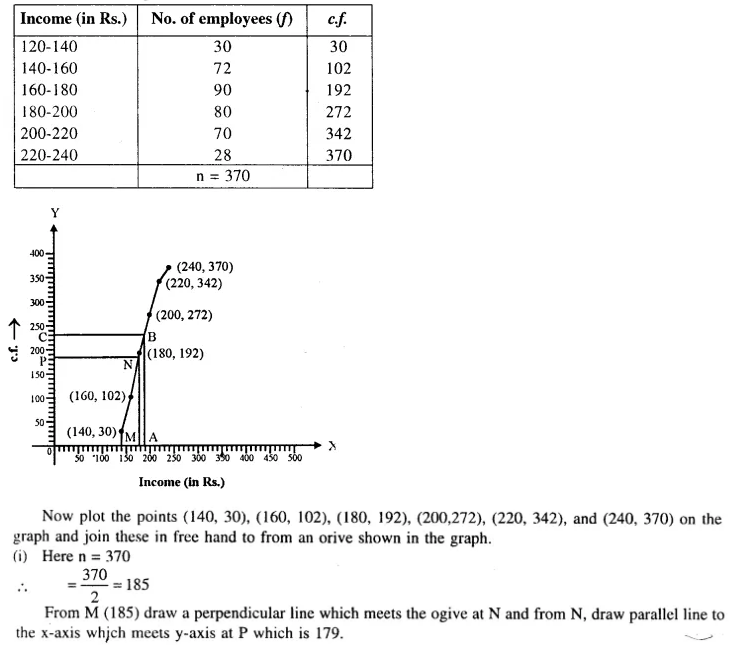
Question 102.
Draw an ogive for the following distribution :

Use the ogive drawn to determine :
(i) the median income,
(ii) the number of employees whose income exceeds Rs. 190.
Solution:

Question 103.
The result of an examination are tabulated below :

Draw the ogive for above data and from it determine :
(i) the number of candidates who got marks less than 45.
(ii) the number of candidates who got marks more than 75.
Solution:

Probability

Question 104.
A bag contains a red ball, a blue ball and a yellow ball, all the balls being of the same size. If a ball is drawn from the bag, without looking into it, find the probability that the ball drawn is
(i) yellow
(ii) red
(iii) blue
Solution:

Question 105.
A bag contains 6 red balls, 8 blue balls and 10 yellow balls, all the balls being of the same size. If a ball is drawn from the bag, without looking into it, find the probability that the ball drawn is
(i) yellow
(ii) red
(iii) blue
(iv) not yellow
(v) not blue
Solution:

Question 106.
Two dice are thrown at the same time. Write down all the possible outcomes. Find the probability of getting the sum of two numbers appearing on the top of the dice as :
(i) 13
(ii) less than 13
(iii) 10
(iv) less then 10
Solution:

Question 107.
Five cards : the ten, jack, queen, king and ace. of diamonds are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen ?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is (a) an ace ? (b) a queen ?
Solution:

Question 108.
(i) A lot of 20 bulbs contains 4 defective bulbs, one bulb is drawn at random, from the lot. What is the probability that this bulb is defective ?
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapterwise Revision Exercises  are helpful to complete your math homework.