Rational and Irrational Numbers
Both rational and irrational numbers are real numbers.
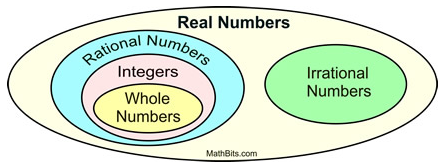
This Venn Diagram shows the relationships between sets of numbers. Notice that rational and irrational numbers are contained in the large blue rectangle representing the set of Real Numbers.
Rational Numbers
A rational number is a number that can be expressed as a fraction or ratio.
The numerator and the denominator of the fraction are both integers.
Examples of rational numbers are:
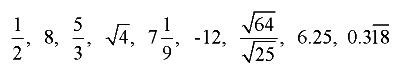
A rational number can be expressed as a ratio (fraction) with integers in both the top and the bottom of the fraction.
When the fraction is divided out, it becomes a terminating or repeating decimal. (The repeating decimal portion may be one number or a billion numbers.)
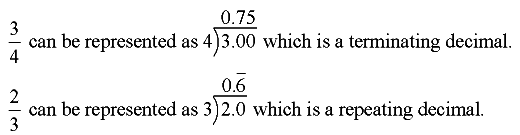
Rational numbers on number line:
A number line is a straight line diagram on which every point corresponds to a real number.
Since rational numbers are real numbers, they have a specific location on a number line.

To convert a repeating decimal to a fraction:

To show that the rational numbers are “dense”:
(The term “dense” means that between any two rational numbers there is another rational number.)
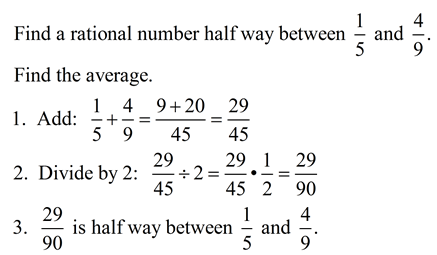
Irrational Numbers
An irrational number cannot be expressed as a fraction.
- Irrational numbers cannot be represented as terminating or repeating decimals.
- Irrational numbers are non-terminating, non-repeating decimals.
- Examples of irrational numbers are:
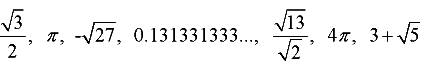
Note: Many students think that π is the terminating decimal, 3.14, but it is not. Yes, certain math problems ask you to use π as 3.14, but that problem is rounding the value of to make your calculations easier. π is actually a non-ending decimal and is an irrational number.
There are certain radical values which fall into the irrational number category.
For example, √2 cannot be written as a “simple fraction”
which has integers in the numerator and the denominator.
As a decimal, √2 = 1.414213562373095048801688624 …
which is a non-ending and non-repeating decimal, making √2 irrational.
Irrational Numbers on a Number Line:
By definition, a number line is a straight line diagram on which every point corresponds to a real number.
Since irrational numbers are a subset of the real numbers, and real numbers can be represented on a number line, one might assume that each irrational number has a “specific” location on the number line.
“Estimates” of the locations of irrational numbers on number line:

Maths