Pythagorean Theorem
THEOREM:
In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.
(c2 = a2 + b2)
It is believed that this theorem was known, in some form, long before the time of Pythagoras. A thousand years before Pythagoras, the Babylonians recorded their knowledge of the theorem on clay tablets. The Egyptians used the concept of the theorem in the building of the pyramids. In 1100 B.C. China, Tschou-Gun knew of this theorem.
It was, however, Pythagoras who generalized the theorem to all right triangles and is credited with its first geometrical demonstration. Consequently, the theorem bears his name.
Geometrical Proof: The Pythagorean Theorem has drawn a good deal of attention from mathematicians. There are hundreds of geometrical proofs (or demonstrations) of the theorem, with even a larger number of algebraic proofs.
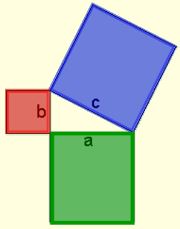Geometrically, the Pythagorean Theorem can be interpreted as discussing the areas of squares whose sides are the sides of the triangle (as seen in the picture at the left). The theorem can be rephrased as, “The (area of the) square described upon the hypotenuse of a right triangle is equal to the sum of the (areas of )the squares described upon the other two sides.”
Converse:
Theorem: If a triangle is a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.
Converse: If the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, the triangle is a right triangle.
Pythagorean Triples: There are certain sets of numbers that have a very special property in connection to the Pythagorean Theorem. Not only do these numbers satisfy the Pythagorean Theorem, but any multiples of these numbers also satisfy the Pythagorean Theorem.
For example: the numbers 3, 4, and 5 satisfy the Pythagorean Theorem. If you multiply all three numbers by 2 (you will get 6, 8, and 10), these new numbers ALSO satisfy the Pythagorean theorem.
The special sets of numbers that possess this property are called Pythagorean Triples.
The most common Pythagorean Triples are:
There are equations for generating Pythagorean Triples. Such equationss are used by computer programmers to generate lists of Pythagorean Triples. Equations: When m and n are both positive integers and m < n, Pythagorean Triples can be generated using the following equations where a and b will be the legs of the right triangle and c will be the hypotenuse.
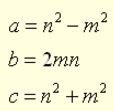It can be shown that the results from these equations do, in fact, satisfy the Pythatorean Theorem:
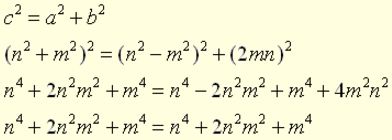
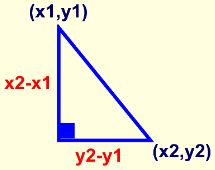
Connection to the Distance Formula: The Pythagorean Theorem serves as the basis for determining the distance between two points in the Cartesian plane, called the Distance Formula.
If (x1, y1) and (x2, y2) are points in the plane, then the distance between them can be determined using the Pythagorean Theorem.
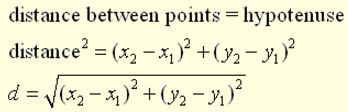
Generalization of the Law of Cosines: The Pythagorean theorem is a specific case of the more general theorem relating the lengths of sides in any triangle, called the Law of Cosines.
Law of Cosines: c2 = a2 + b2 – 2ab cosC
When angle C is 90°, cosC equals 0 and the formula becomes to the Pythagorean Theorem.
In non-Euclidean Geometries: While the Pythagorean Theorem is of prime importance to Euclidean Geometry (and is derived from its axioms), it does not hold in non-Euclidean Geometries.