PRIME FACTORISATION
Prime factorisation is the process by which a composite number is rewritten as the product of prime factors.
 Example 1: Find out the prime factorisation of 30.
Example 1: Find out the prime factorisation of 30.
First we will see whether the given number is divisible by a least prime number.
Yes, it is, because the digit at its ones place is 0.
30 = 2 × 15
We have, 15 = 3 × 5

So, the factors of 30 are
∴ 30 = 2 × 3 × 5
2, 3, and 5 are prime factors of 30.
Example 2: Let us consider another number 56.
56 = 2 × 28 = 2 × 2 × 14 = 2 × 2 × 2 × 7
2 and 7 are prime factors of 56.
Prime factorisation of a bigger number using short division method
Let us Explain it by taking an example.
Example 1: Express 256 in prime factorisation.
Divide 256 starting from the smallest prime number which can divide it. Repeat the process till the quotient is no more divisible by the prime number.
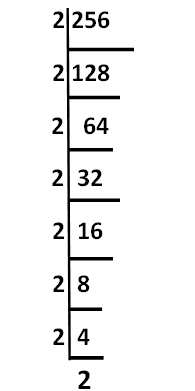
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Example 2: Express 540 in prime factorisation.

540 = 2 × 2 × 3 × 3 × 3 × 5
HIGHEST COMMON FACTOR (HCF)
Rita and Rina went to a stationery shop. Rita purchased 2 pencils, 2 pens, and 1 eraser. Rina purchased 2 pencils, 1 scale, and 1 pen. The common stationery bought by both are pencils and pens. Out of these, common stationery with maximum number is pencil (2). Thus, HCF is 2 pencils.
Highest common factor of two natural numbers is the largest common factor, or divisor of the given natural numbers. In other words, HCF is the greatest element of the set of common factors of the given numbers.

Example: Let us consider two numbers 45 and 63.
Common factors of 45 and 63 = 1, 3, 9
Highest common factor = 9.
So, the HCF of 45 and 63 is 9.
HCF by prime factorisation method
Let us consider two numbers 72 and 48.
To find prime factorisation, we have to follow these steps.
Step 1: Find the prime factorisation of both the numbers.

Step 2: Find the common prime factors of the given numbers.
Common factors = 2, 2, 2, 3
Step 3: Multiply all the common factors to find out the HCF.
∴ HCF = 2 × 2 × 2 × 3
= 24
The HCF of two or more numbers is the greatest common factor of all the given numbers.
HCF by long division method
To find HCF using long division method of two
numbers, follow the steps given below.
Step 1: Divide the greater number by smaller number.
Step 2: Take remainder as divisor and the divisor as dividend.
Step 3: Continue the process till you get 0 as the remainder.
Step 4: The last divisor will be the required HCF of the given numbers.
Example 1: Find the HCF of 198 and 360 using the long division method.
Solution:

Here, the last divisor is 18.
So, HCF of 198 and 360 = 18.
Example 2: Find the greatest number which Exactly divides the numbers 280 and 1245, leaving remainders 4 and 3 respectively.
Solution: Since 4 and 3 are the remainders when 280 and 1245 are divided by the required number.
∴ 280 – 4 = 276 and 1245 – 3 = 1242 will be Exactly divisible by the required number.
We find the HCF of 276 and 1242.
276 = 2 × 2 × 3 × 23
1242 = 2 × 3 × 3 × 3 × 23
∴ HCF = 2 × 3 × 23 = 138
The HCF of 276 and 1242 = 138
So, the required number is 138.
LOWEST COMMON MULTIPLE OR LEAST COMMON MULTIPLE (LCM)
Teena jogs every third day and Meena jogs every fifth day. They are both jogging today. After how many days will they jog together again?
Teena will jog on 3rd day, 6th day, 9th day,…
Meena will jog on 5th day, 10th day, 15th day,…
For Teena, multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33,…
For Meena, multiples of 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45,…
This means, they will jog together after 15 days,
30 days, 45 days, etc. Therefore, 15, 30, 45,… are common multiples of 3 and 5 but the least (lowest) common multiple of 3 and 5 is 15. Hence, after 15 days, they will jog together again.
Least common multiple (LCM) of two natural numbers a and b is the smallest natural number which is a multiple of both a and b.
Since it is a multiple, it can be divided by a and b without leaving a remainder.

Example 1: Find the LCM of 4, 8, and 12.
Solution: Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48,…
Multiples of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72,…
Multiples of 12 = 12, 24, 36, 48, 60, 72, 84,…
Common multiples = 24,48, 72
Lowest common multiple = 24
So, the LCM of 4, 8,12 is 24.
Example 2: Find the LCM of 25 and 30.
Solution: Multiple of 25 = 25, 50, 75, 100, 125, 150, 175, 200
Multiples of 30 = 30, 60, 90, 120, 150, 180, 210, 240
Common multiples of 25 and 30 = 150, 300,…
Least common multiple =150
So, the LCM of 25 and 30 is 150.
Finding LCM by prime factorisation method
To find the LCM by prime factorisation method, we follow the following steps:
Step 1: Express the given numbers as the product of prime numbers.
Step 2: Count the maximum number of times each factor appears then multiply them.
Step 3: The product of those factors is the least common multiple (LCM).
Example 1: Find the LCM of 28, 44, and 132 by the prime factorisation method.
Solution:
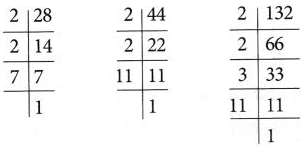
Prime factorisation of 28 = 2 × 2 × 7
Prime factorisation of 44 = 2 × 2 × 11
Prime factorisation of 32 = 2 × 2 × 3 × 11
Here 2 appears twice.
3, 7, and 11 appear once.
∴ LCM = 2 × 2 × 3 × 7 × 11 = 924
Example 2: Find the LCM of 72, 90, and 108 by factorisation method.
Solution:

Prime factorisation of 72 =2 × 2 × 2 × 3 × 3
Prime factorisation of 108 = 2 × 2 × 3 × 3 × 3
Here, 2 appears three times, 3 appears three times, and 5 appears once.
∴ LCM = 2 × 2 × 2 × 3 × 3 × 3 × 5
= 1080
LCM by common division method
To find the LCM by common division method, we follow these steps.
Step 1: Arrange the numbers in a row separated by commas.
Step 2: Choose a least prime number that divides at least one of the given numbers.
Step 3: Divide the numbers by the number chosen in step 2 and carry forward the undivided numbers.
Step 4: Repeat the process till the number left in the last row is 1.
Step 5: Multiply all the prime divisors to get the LCM.
Example 1: Find the LCM of 102, 170, and 136 by common division method.
Solution:

LCM = 2 × 2 × 2 × 3 × 5 × 17 = 2040
Example 2: Find the LCM of 11, 22, 24, and 36.
Solution:

Prime factorisation of 90 = 2 × 3 × 3 × 5
LCM = 2 × 2 × 3 × 11 × 2 × 3 = 792
Example 3: Find the least number which when divided by 20,24, and 36, leaves a remainder of 18 in each case.
Solution: The least number which is exactly divisible by 20, 24, and 36 is the LCM of these numbers. We first find the LCM of 20, 24, and 36.

∴ LCM = 2 × 2 × 3 × 2 × 3 × 5 = 360
But, the required number is a number that leaves a remainder of 18 in each case.
That means the required number is 18 more than the LCM.
∴ Required number = 360 + 18 = 378
Prime Factors Using Factor Tree Example Problems With Solutions
Example 1: Find the prime factors of 540
Sol.
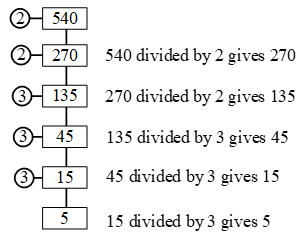
∴ 5 is a prime number and so cannot be further divided by any prime number
540 = 2 × 2 × 3 × 3 × 3 × 5 = 22 × 33 ×5
Example 2: Find the prime factors of 21252
Sol.
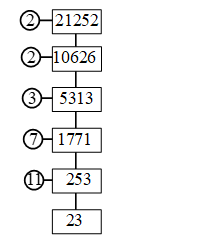
∴ 21252 = 2 × 2 × 3 × 7 × 11 × 23
= 22 × 3 × 11 × 7 × 23.
Example 3: Find the prime factors of 8232
Sol.
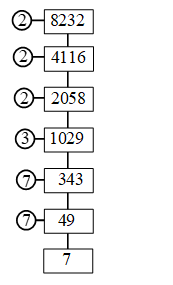
∴ 8232 = 2 × 2 × 2 × 3 × 7 × 7 × 7
= 23 × 3 × 73.
Example 4: Find the missing numbers a, b and c in the following factorisation:
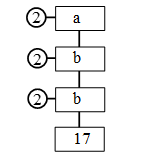
Can you find the number on top without finding the other ?
Sol. c = 17 × 2 = 34
b = c × 2 = 34 × 2 = 68 and
a = b × 2 = 68 × 2 = 136
i.e., a = 136, b = 68 and c = 34.
Yes, we can find the number on top without finding the others.
Reason: The given numbers 2, 2, 2 and 17 are the only prime factors of the number on top and so the number on top = 2 × 2 × 2 × 17 = 136