Plus Two Physics Notes Chapter 2 Electric Potential and Capacitance is part of Plus Two Physics Notes. Here we have given Plus Two Physics Notes Chapter 2 Electric Potential and Capacitance.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Physics Notes |
| Chapter | Chapter 2 |
| Chapter Name | Electric Potential and Capacitance |
| Category | Plus Two Kerala |
Kerala Plus Two Physics Notes Chapter 2 Electric Potential and Capacitance
Introduction
The electric field strength is a vector quantity, while the electric potential is a scalar quantity. Both these quantities are interrelated.
Electrostatic Potential
1. Electric potential: The electric potential at a point is the work done by an external agent in moving a unit positive charge from infinity to that point against the electric field (without acceleration)
Explanation: If W is the work done in moving a charge ‘q’ from infinity to a point, then the potential at
that point is, V = \(\frac{w}{q}\)
Potential difference: Electric potential difference between two points is the work done in moving a unit positive charge from one point to another.
The potential difference between points A and B is
VAB = VA – VB
VA and VB are the potentials at points A and B respectively.
Potential energy difference: Potential energy difference is the work done to bring a q charge from one point to another point without acceleration.
Relation between potential difference and potential energy difference:
![]()
where UA and UB are the potential energies at points A and B respectively.
Electric field is conservative: Electric field is conservative. A conservative field is defined as the field in which work done is zero in a complete round trip.
(or)
A conservative field is one in which work done is independent of path.
Potential Due To A Point Charge

Let P be a point at a distance Y from a charge +q. Let A be a point at a distance ‘x’ from q , and E is directed along with PA. Consider a positive charge at A. Then the electric field intensity at A’ is given by
![]()
If this unit charge is moved (opposite to E) through a distance dx, the work done dw = – Edx
[-ve sign indicates that dx is opposite to E ]
So the potential at ‘P’ is given by
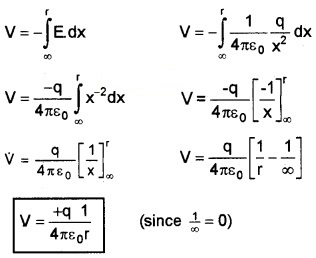
Potential due to an electric dipole
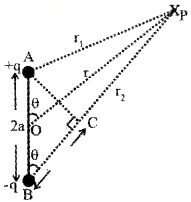
Consider dipole of length ‘2a’. Let P be a point at distance r1 from +q and r2 from -q. Let ‘r’ be the distance of P from the centre ‘O’ of the dipole. Let θ be angle between dipole and line OP.

Therefore total potential,
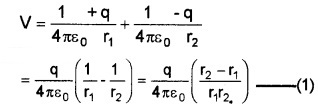
From ∆ABC , we get (r2 – r1) = 2a cosθ
we can also take r2 = r1 = r (since ‘2a’ is very small) Substituting these values in equation (1), we get

Case 1: If the point lies along the axial line of the dipole, then θ = 0°
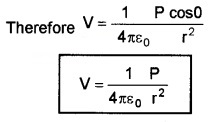
Case 2: If the point lies along the equatorial line of the dipole, then θ = 90°
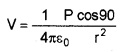
V = 0
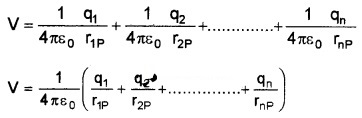
Potential Due To A System Of Charges
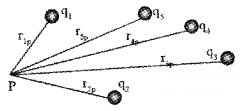
Consider a system of charges q1, q2,……,qn with position vectors r1P, r2P……..,rnP relative to some origin. The potential V1 at P due to the charge q1 is
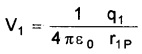
where r1P is the distance between q1 and P. Similarly, the potential V2 at P due to q2,
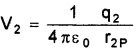
where r2P is the distances of P from charges q2. By the superposition principle, the potential V at P due to the total charge configuration is the algebraic sum of the potentials due to the individual charges
ie. V = V1 + V2 +……+ Vn
Equipotential Surface
The surface over which the electric potential is same is called an equipotential surface.
Properties:
- Direction of electric field is perpendicular to the equipotential surface.
- No work is done to move a charge from one point to another along the equipotential surface.
Example:
- Surface of a charged conductor.
- All points equidistant from a point charge.
Equipotential surfaces for a uniform electric filed:

1. Relation Between Electric Field And Potential:
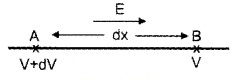
Consider two points A and B, separated by very small distance dx. Let the potential at A and B be V+ dV and V respectively. The electric field is directed from A to B.
If a unit +ve charge is moved through a distance ‘dx’ against this field, work done,
dw = -Edx _____ (1)
For unit charge dw = dv
∴ dv = – Edx
or
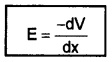
Electric field intensity at a point is the negative rate of change of potential with distance.
Potential Energy Of System Of Charges
1. Potential Energy of System of Two Charges:
The potential energy of a system of two charges is defined as the work done in assembling this system of charges at the given position from infinite separation.

Consider two charges q1 and q2 separated by distance r. Imagine q1 to be at A and q2 at infinity. Electric potential at B due to charge q1 is given by
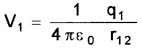
which is the work done in bringing unit positive charge from infinity to B. Therefore the work done in bringing charge q2 from infinity to B is
W = potential difference × charge
W = (V1 – V∞)q2
potential at inf infinity. V∞ = 0
W = V1 × q2
\(W=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{12}}\)
This work done is stored as potential energy. Hence potential energy between the charges q1 and q2
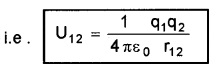
2. Potential Energy of System of Three Charges:
Consider three charges q1, q2, and q3 separated by distances r12, r23 and r13.
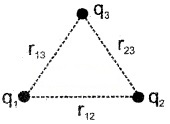
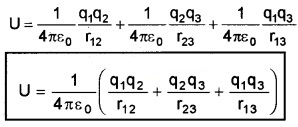
The electric potential energy of this system is the sum of potential of each pair. Hence we can write
U = U12 + U23 + U13
Potential Energy In An External Field
1. Potential energy of a single charge:
Consider a point O in an electric field. Let V be the electric potential at O. Hence work done in bringing a charge q from infinity to the point O is,
W = Vq.
This work done is stored in the form of electrostatic potential energy (U) of the charge q.
∴ The potential energy of the charge q in an electric field is U = Vq
Where V is the potential at that point.
2. Potential energy of a system of two charges in an electric field:
Consider an electric field. Let 1 and 2 be two points in the field and V1 and V2 be the potential at these points. Two charges q1 and q2 are located at 1 and 2.
Potential energy of the charge q1 in the external filed is, U1 = V1 q1
Potential energy of the charge q2 in the external field is, U2 = V2q2
Potential energy between the system of two charges q1 and q2
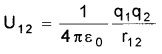
where r12 is the distance between the charges According to the principle of superposition, the potential energy of the system of two charges in an electric field is
U = U1 + U2 + U12
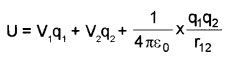
3. Potential energy of a dipole in an external field:
Consider a dipole of dipole moment ‘P’ suspended in a uniform electric field of intensity ‘E’. Let θ be the angle between P and E.
Then we know torque τ = PE sinθ
Let the dipole be turned through an angle dθ
then work done dw = τdθ
= PE sinθ dθ
Total work done in rotating the dipole from θ1 to θ2
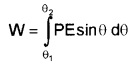
W = PE (cosθ1 – cosθ2)
This work done is stored as potential energy.
Electrostatics Of Conductors
The electrostatic properties of conductors are given below:
1. Inside a conductor, the electrostatic field is zero:
In the static situation, there is no current found inside the conductor. Hence we conclude that the electric field is zero inside the conductor The vanishing of the electric field inside the metal cavity is called electrostatic shielding.
2. At the surface of a charged conductor, the electrostatic field must be normal to the surface at every point.
3. The interior of a conductor can have no excess charge in the static situation.
4. Electrostatic potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface.
5. Electric field at the surface of a charged conductor
\(\bar{E}=\frac{\sigma}{\varepsilon_{0}} \hat{n}\)
where σ is the surface charge density and is a unit vector normal to the surface in the outward direction.
6. Electric field inside a metal cavity is zero. Vanishing of electric inside a metal cavity is called electrostatic shielding. Sensitive electrical instruments can be protected from external electricfield by placing it in a metal cavity.
Dielectrics And Polarization
Dielectrics (insulator): Dielectrics are non-conducting substances. They have no charge carriers. The molecules of dielectrics may be classified into two classes.
- Polar molecule
- Nonpolar molecule
Electric field due to a dipole at a point on the perpendicular bisector of the dipole (at a point on the equatorial line).
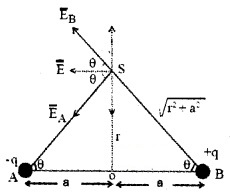
Consider a dipole of dipole moment P = 2aq. Let ‘S’ be a point on its equatorial line at a distance ‘r’ from its centre. The magnitudes of electric field at ‘S’ due to +q and -q are equal and acts as shown in figure. To find the resultant electric field resolve.

Their normal components cancel each otherwhere as their horizontal components add up to give the resultant field at ‘S’.
E = EAcos θ + EBcos θ = 2 EB cos θ

The direction of the field due to the dipole at a point on the equatorial line is opposite to the direction of dipole moment.
1. Dielectrics in external electric field
(a) Nonpolar dielectrics in external field:
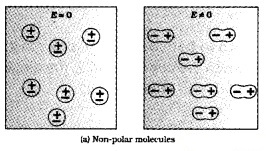
Considers nonpolar dielectrics in an external electricfield. In electricfield, the positive and negative changes of a nonpolar molecule are displaced in opposite directions. Thus dipole moment is induced in a nonpolar molecule. The induced dipole moments of different molecules add up giving a net dipole moment.
(b) Polar dielectrics in external electric field:
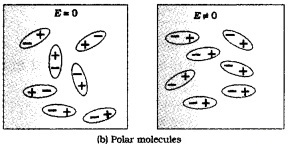
The permanent dipoles in a polar dielectric are arranged randomly. So total dipole moment is zero. But when we apply external electric field, the individual dipole tends to align in the direction of electricfield. The induced dipole moments of different molecules add up giving a net dipole moment.
Electric susceptibility: Non-polar dielectrics and polar dielectrics can produce net dipole moment in the external electric field. The dipole moment per unit volume is called polarization and is denoted as P. For linear isotropic dielectrics.
\(\bar{P}=\chi_{0} \bar{E}\)
where χe is a constant and is known as the electric susceptibility of the dielectric medium.
How does the polarized dielectric modify the external field inside it?
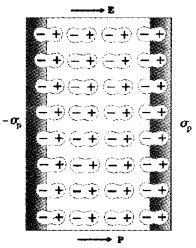
Consider a dielectric slab placed inside a uniform external electric field E0. This field produces a uniform polarization as shown in the figure. Any region inside the dielectric, the net charge is zero.
This is due to the cancellation of positive charge of one dipole with negative charge of adjacent dipole. But the positive ends of the dipole do not cancel at right surface and the negative ends at the left surface.
This surface charges (-σp and +σp) produce a field \(\left(\vec{E}_{i n}\right)\) opposite to the external field. Hence total electric field is reduced inside the dielectric field which is shown in the figure below.
ie; E0 + Ein ≠ 0

How does a metal modify the external electric field applied on it?
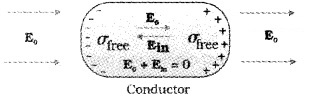
When a conductor placed in a electric field, the free charges are moved in opposite direction as shown in figure. This rearrangement of charges in a metal produce an internal field (Ein) inside the metal. This internal field cancels the external field. Thus the net electric field inside the metal becomes zero.
ie; E0 + Ein = 0
Capacitors And Capacitance
Capacitor: Capacitor is a system of two conductors separated by an insulator for storing electric charges.
Capacitance of a capacitor:
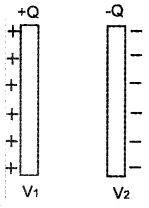
Consider two-conductor having charges +Q and -Q and potentials V1 and V2. The amount of charge Q on a plate is directly proportional to the potential difference (v1 – v2) between the plates,
ie. Q α V1 – V2
(or) Q α V (where V = V1 – V2)
![]()
The constant C is called the capacitance of the capacitor. If V = 1, we get Q = C. Hence capacitance of a capacitor may be defined as the amount of charge required to raise the potential difference between two plates by one volt.
Dielectric strength:
What happens to the charge stored in capacitor when the p.d. between two plates increases?
When the p.d. between two plates increases, electric field in between two plates increases. This high electric field can ionize the surrounding air (or medium) and accelerate the charges to the oppositely charged plates and neutralize the charge on the plate. This is called electric break down.
The maximum electric field that a dielectric medium can withstand without break down (of its insulating property) is called its dielectric strength. The dielectric strength of air is 3 × 106 v/m.
The Parallel Plate Capacitor
Electric field due to a capacitor:
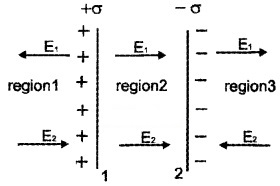
Consider a parallel plate capacitor consists of two large conducting plates 1 and 2 separated by a small distance d. Let +σ and -σ be the surface charge densities of first and second plates respectively. (Here, we take, electric field towards right is taken as positive and left as negative.)
Region I: This region lies above plate 1.
E = E+ + E– ie.
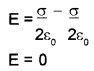
Region II: This region lies below plate 2.
E = E– + E+ ie.
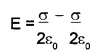
E = 0
Electric field in between two plates: In the inner region between plates 1 and 2, the electric field due to two charged plates add up.
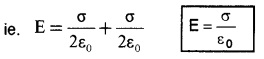
(a) Expression for capacitance of a capacitor: Potential difference between two plates
V= Ed

Effect Of Dielectric On Capacitance
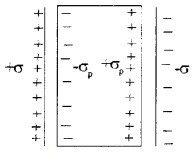
Consider a capacitor of area A and charge densities +σ and -σ. Let d be the distance between the plates. If a dielectric slab is placed inside this capacitor, it undergoes polarization. Let +σp and -σp be polarized charge densities due to polarization.
Due to polarization electric field in between the plate becomes
\(E=\frac{\sigma}{K \varepsilon_{0}}\) _____(1)
The potential difference between the plates,
V = Ed _____(2)
Sub (1) in (2)
\(\mathrm{V}=\frac{\sigma}{\mathrm{K} \mathrm{s}_{0}} \mathrm{d}\)
Then the capacitance of capacitor
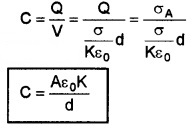
The product ε0 K is the permittivity of the medium.
Combination Of Capacitors
1. Capacitors in series: Let three capacitors C1, C2 and C3 be connected in series to p.d of V. Let V1, V2 and V3 be the voltage across C1, C2, and C3.
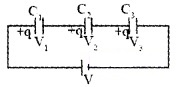
The applied voltage can be written as
V = V1 + V2 + V3 ______(1)
Charge ‘q’ is same as in all the capacitor. So,
![]()
Substituting these values in (1),
![]()
If these capacitors are replaced by a equivalent capacitance ‘C’, then
V = \(\frac{q}{C}\)
Hence eq(2) can be written as

Effective capacitance is decreased by series combination.
2. Capacitors in parallel:
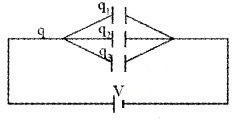
Let three capacitors C1, C2 and C3 be connected in parallel to p.d of V. Let q1, q2, and q3 be the charges on C1, C2 and C3.
If ‘q’ is the total charge, then’q’can be written as
q = q1 + q2 + q3
But q1 = C1V, q2 = C2V and q3 = C3V
Hence eq (2) can be written as
CV = C1V + C2V + C3V
![]()
Effective capacitance increases in parallel connection.
Energy Stored In A Capacitor
Energy of a capacitor is the work done in charging it. Consider a capacitor of capacitance ‘C’. Let ‘q’ be the charge at any instant and ‘V’ be the potential. If we supply a charge ‘dq’ to the capacitor, then work done can be written as,
dw = Vdq
dw = \(\frac{q}{C}\)dq (since V = \(\frac{q}{C}\))
∴ Total work done to charge the capacitor (from ‘0’ to ‘Q’) is

But Q = CV
W = \(\frac{1}{2}\) CV2
This work done is stored in the capacitor as electric potential energy.
∴ Energy stored in the capacitor is,
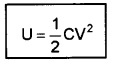
Van De Graff Generator
Van de Graff generator is used to produce very high voltage.
Principle: If two charged concentric hollow spheres are brought in to contact, charge will always flow from inner sphere to the outer sphere.
Construction and working:
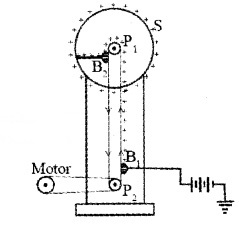
The vande Graff generator consists of a large spherical metal shell, placed on an insulating stand. Let p1 and p2 be two pulleys. Pulley p1 is at the center of the spherical shell S. A belt is wound around two pulleys p1 and p2. This belt is rotated by a motor. Positive charges are sprayed by belt. Brush B2 transfer these charges to the spherical shell. This process is continued. Hence a very high voltage is produced on the sphere.
Why does the charge flow from inner sphere to outer sphere?

Let ‘r’ and ‘R’ be the radius of inner sphere and outer sphere carrying charges q and Q respectively.
The potential on the outer sphere,
V(R) = Potential due to outer charge + potential due to inner charge
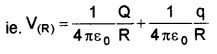
Potential on the inner sphere. V(r) = Potential due to outer charge + Potential due to inner charge
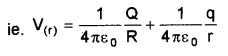
∴ Potential difference between the two spheres
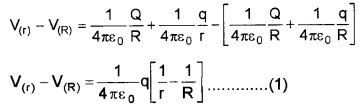
The above equation shows that the inner sphere will be always at a higher potential. Hence, the charge always flows from the inner sphere to the outer sphere.
We hope the Plus Two Physics Notes Chapter 2 Electric Potential and Capacitance help you. If you have any query regarding Plus Two Physics Notes Chapter 2 Electric Potential and Capacitance, drop a comment below and we will get back to you at the earliest.