Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter is part of Plus Two Physics Notes. Here we have given Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Physics Notes |
| Chapter | Chapter 11 |
| Chapter Name | Dual Nature of Radiation and Matter |
| Category | Plus Two Kerala |
Kerala Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter
Introduction
The discovery of cathode rays by Rontgen and discovery of electrons by JJ Thomson were important milestones in the study of atomic structure.
Electron Emission
We know that metals have free electrons. The free electrons cannot normally escape out of the metal surface. If an electron attempts to come out of the metal, the metal surface acquires a positive charge. This positive surface held electrons inside the metal surface.
Work function:
When we give energy to electron in a metal, it can come out of metal. This minimum energy required by an electron to escape from the metal surface is called the work function of the metal. It is generally denoted by Φ0(hν0) and measured in eV (electron volt).
Electron volt:
One electron volt is the energy gained by an electron when it has been accelerated by a potential difference of 1 volt
1 eV = 1.602 × 10-19J.
This unit of energy is commonly used in atomic and nuclear physics.
Different types of electron emission:
The minimum energy required for the electron emission from the metal surface can be supplied by any one of the following methods.
(i) Thermionic emission:
Electrons can come out of metal surface, if heat energy is given to metal.
(ii) Field emission:
By applying a very strong electric field (of the order of 108 Vm-1) to a metal, electrons can be pulled out of the metal.
(iii) Photoelectric emission:
When light (of suitable frequency) incident on a metal surface, electrons are emitted from the metal surface. These electrons are called photoelectrons. This phenomena is called photo electric effect.
Photoelectric Effect
1. Hertz’s observations:
The phenomenon of photoelectric emission was discovered by Heinrich Hertz in 1887, Heinrich Hertz observed that when light falls on a metal surface, electrons escape from the metal surface.
2. Hallwachs’ and Lenard’s observations:
Wilhelm Hallwachs and Philipp Lenard investigated the phenomenon of photoelectric emission in detail. The experimental set up consist of two metal plates (cathode and anode) inside a evacuated glass tube as shown in figure.
They observed that current flpws in the circuit when emitter plate (C) was illuminated by UV radiation. It means that when light incident on a metal plate electrons are emitted. These electrons move towards the anode and results in current flow.
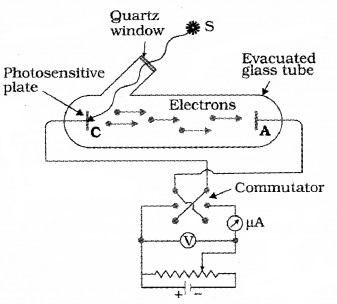
They also observed that, when a negatively charged zinc plate is illuminated by UV light, it becomes chargeless. He also observed that uncharged Zn plate becomes positively charged when it is illuminated with UV light.
From these observations they concluded that the particles emitted carry negative charge.
Threshold frequency:
The minimum frequency (ν0) required to produce photoelectric effect is called the threshold frequency. It depends on the nature of material.
Experimental Study Of Photoelectric Effect
The experimental setup:
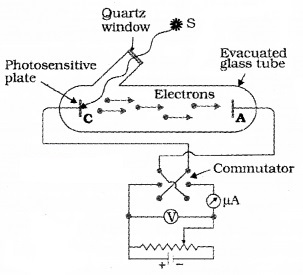
The experimental arrangement consists of two zinc plates enclosed in a quartz bulb. The plates are connected to a battery through a micro ammeter. When ultraviolet light is incident on the cathode plate, the micrometer indicates a current in the circuit.
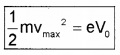
When the anode is made negative (with respect to cathode) the current decreases and at a certain voltage (V0), current is completely stopped. This voltage V0 is called stopping potential. At this stage,
\(\frac{1}{2}\) mVmax2 = eV0
where vmax is the maximum kinetic energy of photo electrons.
1. Effect of intensity of light on photocurrent Experiment:
In this experiment the collector A is maintained at a positive potential. The frequency of the incident radiation and the accelerating potential are kept at fixed.
Then change the intensity of light and measure photoelectric current in each time. Draw a graph between photo current and intensity of light. We get a graph as shown in figure.
Observations:
This graph shows that photocurrent increases linearly with intensity of incident light.
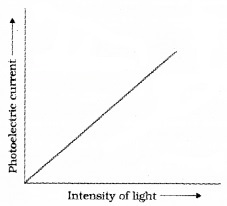
Conclusion:
The photocurrent is directly proportional to the number of photoelectrons emitted per second. This implies that the number off Photoelectrons emitted per second is directly proportional to the intensity of incident radiation.
2. Effect of potential on photoelectric current Experiment:
Keep the plate A at positive accelerating potential. Then illuminate the plate C with light (of fixed frequency v and fixed intensity I1). Then vary the positive potential of plate A gradually and measure the resulting photocurrent each time.
When the photo current reaches maximum, the polarity of plates are reversed and thus apply a negative potential (retarding potential) to plate A.
Again photocurrent is measured by varying the retarding potential till photocurrent reaches zero. The experiment is repeated for higher intensity I2 and I3 keeping the frequency fixed.
Observations:
As accelerating potential increases photo current increases. At a particular anode potential photocurrent reaches maximum. Further increase in accelerating potential does not increase photo current.
When we apply negative potential to A, photo electrons get retarded and hence photocurrent decreases. At particular retarding potential photocurrent becomes zero. This potential is called cut off or stopping potential.
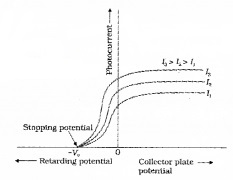
The graph of anode potential with photo current:
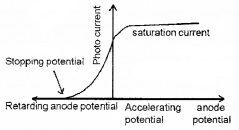
The saturation current is found to be large at higher intensity (because photo current is directly proportional to intensity). But stopping potential is same for different intensity at fixed frequency, (ie. for a given frequency of incident radiation stopping potential is independent of its intensity).
Note:
a. The maximum value of photo current is called saturation current (Isat).
b. The retarding anode potential at which photo current reaches zero is called stopping potential (V0).
When retarding potential is applied, only most energetic electrons can reach collector plate A. At stopping potential no electrons reach plate A, ie stopping potential is sufficient to repel the electron with maximum kinetic energy
c. The stopping potential or maximum value of KE depends only on frequency of incident light, not on its intensity. Hence stopping potential is same for different intensity at constant frequency.
d. At zero anode potential, photocurrent is not zero, ie photo electric effect takes place even if anode potential is not applied.
3. Effect of frequency of incident radiation on stopping potential:
Experiment:
In this experiment, we adjust the intensity of light at various frequencies (say ν1, ν2 and ν3 such that ν1 < ν2 < ν3) and study the variation of photocurrent with collector plate potential.
Observations:
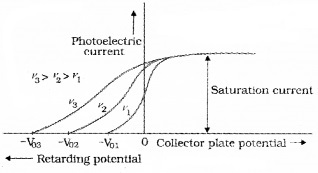
For frequencies ν1, ν2 and ν3 (ν1 < ν2 < ν3) τηε stopping potential are found to be V03 > V02 > V01. It means that stopping potential varies linearly with incident frequency fora given photosensitive material.
The graph of stopping potential with frequency:
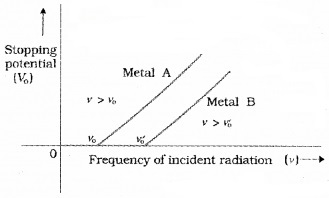
The graph shows that
- The stopping potential V0 varies linearly with the frequency of incident radiation for a given photosensitive material,
- There exists a certain minimum cutoff frequency ν0 for which the stopping potential is zero.
These observations have two implications:
- The maximum kinetic energy of the photoelectrons varies linearly with the frequency of incident radiation, but is independent of its intensity.
- Fora frequency ν of incident radiation, lower than the cutoff frequency ν0, no photoelectric emission is possible even if the intensity is large.
- For a frequency ν0, no photoelectric emission is possible even if the intensity is large. This minimum, cutoff frequency ν0, is called the threshold frequency. It is different for different metals.
Summary of the experimental features and observations:
Laws of photoelectric emission:
- For a given frequency of radiation, number of photoelectrons emitted is proportional to the intensity of incident radiation.
- The kinetic energy of photoelectrons depends on the frequency of incident light but it is independent of the light intensity.
- Photoelectric effect does not occur if the frequency is below a certain value. The minimum frequency (ν0) required to produce photo electric effect is called the threshold frequency.
- Photoelectric effect is an instantaneous phenomenon.
Photoelectric Effect And Wave Theory Of Light
Wage theory of light is not used to explain photoelectric effect. Why?
Reasons
1. According to wave theory, when intensity of incident wave increases, the KE of electron must be increased. This is pgainst the experimental observation of photoelectric effect.
2. According to wave theory, absorption of energy by electron takes place continuously. A large number of electrons absorb energy from the wave at a time.
Hence energy received by a single electron will be small. Hence it takes hours to eject an electron from a metal surface. This delay in photoemission is against the experimental observation.
Einstein’s Photoelectric Equation
Energy quantum of radiation:
Einstein explained photoelectric effect based on quantum theory. According to quantum theory, light contain photons having energy hν, when a photon of energy hr incidents on a metal surface, electrons are liberated.
A small portion of the photon energy is used for work function (Φ) and remaining energy is appeared as K.E of the electron.
By law of conservation of energy, we can write,
Photon energy = work function + K.E of electrons
hν = Φ + \(\frac{1}{2}\) mv2
\(\frac{1}{2}\)mv2 = hν – Φ______(1)
If threshold frequency ν0 is incident, we can take K.E = 0
So eq(1) can be written as
0 = hν0 – Φ
i.e. work function Φ = hν0______(2)
Substituting eq(2) in eq(1) we get
\(\frac{1}{2}\)mv2 = hν – hν0
\(\frac{1}{2}\)mv2 = h(ν – ν0)______(3)
This is Einstein’s Photoelectric equation.
But we know ν = c/λ and ν0 = c/λ0
Substituting these values in eq(3) we get,
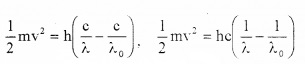
Discussion (explanation of photo electric effect on the basis of Einstein’s photo electric equation):
1. If the intensity of the incident light increases, more number of photons interact with electrons and more number of electrons are emitted. Thus the electric current increases with the intensity of the incident light.
2. For a given metal, Φ0(hν0) is constant. Hence from 1/2mv2 = hν – hν0, we can understand that KE depends on ‘V’ (incident frequency).
3. From this equation 1/2mv2 = hν – hν0. we can understand that photoemission is not possible, if ν < ν0.
4. According to quantum theory, a photon interacts only with a single electron (no sharing of energy takes place) so that there is no time delay in photoelectric emission.
Particle Nature Of Light: The Photon:
The photon picture of electromagnetic radiation is as follows:
- In interaction of radiation with matter, radiation behaves as if it is made up of particles called photons.
- Each photon has energy E and momentum ρ.
- Photon energy is independent of intensity of radiation.
- Photons are electrically neutral and are not deflected by electric and magnetic fields.
- In a photon-particle collision the total energy and total momentum are conserved.
Wave Nature Of Matter
In 1924, the French physicist Louis Victorde Broglie put forward the hypothesis, that moving particles of matter should display wavelike properties under suitable conditions.
The waves associated with material particles are known as matter waves or de-Broglie’s waves. de-Broglie wave is seen with microscopic particles like proton, electron, and neutron, etc. The wave length of matter waves is called de-Broglie wave length.
De-Broglie wave length,
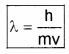
h – Plank’s constant, m – mass of the particle, v – velocity of the particle.
1. Wavelength of matter waves:
The energy of photon E = hν _____(1)
If photon is considered as a particle of mass ‘m’, the energy of photon can be written as
E = mc2 _____(2)
From eq(1) and eq (2) we get
hν = mc2
m = \(\frac{\mathrm{hv}}{\mathrm{c}^{2}}\) ________(3)
Momentum of the electron can be written as
P = mass × velocity ______(4)
Substituting eq (3) in eq(4) ,we get
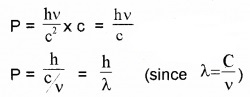
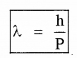
The wave length of electron wave:
If electron of mass ‘m’ and charge ‘e’ is accelerated through a p.d of V volt, the de-Broglie wavelength can be written as
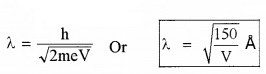
2. Uncertainty Principle:
According to the principle, it is not possible to measure both the position and momentum of an electron (or any other particle) at the same time exactly.
If (∆x) is the uncertainty in position and (∆p) is the uncertainties in momemtum, the product uncertainties is given by
∆x.∆p =\(\frac{h}{2 \pi}\)
The above equation allows the possibility that if ∆x is zero; then ∆p must be infinite in order that the product is nonzero. Similarly, if ∆p is zero, ∆x must be infinite.
The wave packet description of an electron:
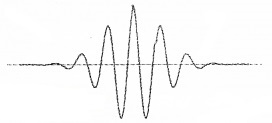
The above wave packet description of matter wave corresponds to an uncertainty in position (∆x) and an uncertainty in momentum (∆p).
Wave packet description for ∆p = 0:
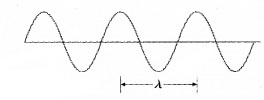
The above wavepacket description of matter wave corresponds to a definite momentum of an electron extends all over space. In this case, ∆p = 0 and
∆x → ∞
Davisson Germer Experiment
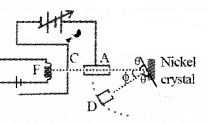
Aim: To confirm the wave nature of electron.
Experimental setup:
The Davisson and Germer Experiment consists of filament ‘F’, which is connected to a low tension battery. The Anode Plate (A) is used to accelerate the beam of electrons. A high voltage is applied in between A and C. ’N’ is a nickel crystal. D is an electron detector. It can be rotated on a circular scale. Detector produces current according to the intensity of incident beam.
Working:
The electron beam is produced by passing current through filament F. The electron beam is accelerated by applying a voltage in between A (anode) and C. The accelerated electron beam is made to fall on the nickel crystal.
The nickel crystal scatters the electron beam to different angles. The crystal is fixed at an angle of Φ = 50° to the incident beam.
The detector current for different values of the accelerating potential ‘V’ is measured. A graph between detector current and voltage (accelerating) is plotted. The shape of the graph is shown in figure.
Analysis of graph:
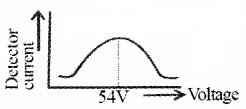
The graph shows that the detector current increases with accelerating voltage and attains maximum value at 54V and then decreases. The maximum value of current at 54 V is due to the constructive interference of scattered waves from nickel crystal (from different planes of crystal). Thus wave nature of electron is established.
Experimental wavelength of electron:
The wave length of the electron can be found from the formula
2d sinθ = nλ ______(1)
From the figure, we get
θ + Φ + θ = 180°
2θ = 180 – Φ, 2θ = 180 – 50°
θ = 65°
for n = 1
equation (1) becomes
λ = 2dsinθ_____(2)
for Ni crystal, d = 0.91 A°
Substituting this in eq. (2), we get
wavelength λ = 1.65 A°
Theoretical wave length of electron:
The accelerating voltage is 54 V
Energy of electron E = 54 × 1.6 × 1019J
∴ Momentum of electron P = \(\sqrt{2 \mathrm{mE}}\)
![]()
= 39.65 × 10-25 Kg ms-1
∴ De-Broglie wavelength λ = \(\frac{h}{P}\)
![]()
Discussion:
The experimentally measured wavelength is found in agreement with de-Broglie wavelength. Thus wave nature of electron is confirmed.
We hope the Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter help you. If you have any query regarding Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter, drop a comment below and we will get back to you at the earliest.