Plus Two Maths Chapter Wise Questions and Answers Chapter 4 Determinants are part of Plus Two Maths Chapter Wise Questions and Answers. Here we have given Plus Two Maths Chapter Wise Questions and Answers Chapter 4 Determinants.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Chapter Wise Questions |
| Chapter | Chapter 4 |
| Chapter Name | Determinants |
| Number of Questions Solved | 45 |
| Category | Plus Two Kerala |
Kerala Plus Two Maths Chapter Wise Questions and Answers Chapter 4 Determinants
Plus Two Maths Determinants Three Mark Questions and Answers
Question 1.
Using properties of determinants prove \(\left|\begin{array}{ccc}{x} & {y} & {x+y} \\{y} & {x+y} & {x} \\{x+y} & {x} & {y}\end{array}\right|\) = -2(x3 + y3).
Answer:
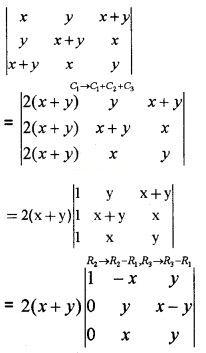
= 2(x + y)(-x2 + xy – y2) = -2(x3 + y3).
Question 2.
If a, b, c are real numbers and \(\left|\begin{array}{lll}{b+c} & {c+a} & {a+b} \\{c+a} & {a+b} & {b+c} \\{a+b} & {b+c} & {c+a}\end{array}\right|\) = 0, Show that a = b = c.
Answer:

2(a + b + c) [(b – c) (c – b) – (b – a) (c – a)] =0 (a+b+c) = 0
(a + b + c) = 0 or (b – c) (c – b) = (b – a) (c – a)
(a + b + c) = 0 or a = b = c.
Question 3.
Solve using properties of determinants.
\(\left|\begin{array}{ccc}{2 x-1} & {x+7} & {x+4} \\{x} & {6} & {2} \\{x-1} & {x+1} & {3}
\end{array}\right|\) = 0
Answer:

⇒ (x – 1) (x2 + x – 6x + 6) = 0
⇒ (x – 1)(x2 – 5x + 6) = 0
⇒ (x – 1) (x – 3) (x – 2) = 0
⇒ x = 1, x = 3, x = 2.
Question 4.
If \(\left|\begin{array}{cc}{3} & {x} \\{x} & {x}\end{array}\right|=\left|\begin{array}{cc}{-2} & {2} \\{4} & {1}\end{array}\right|\), find the value of x.
Answer:
\(\left|\begin{array}{cc}{3} & {x} \\{x} & {x}\end{array}\right|=\left|\begin{array}{cc}{-2} & {2} \\{4} & {1}\end{array}\right|\)
⇒ 3x – x2 = – 2 – 8
⇒ x2 – 3x – 10 = 0
⇒ x = 5, -2.
Question 5.
A = \(\left[\begin{array}{ccc}{1} & {-3} & {1} \\{2} & {0} & {4} \\{1} & {2} & {-2}
\end{array}\right]\)
- Calculate |A| (1)
- Find |adjA| {Hint: using the property A × adjA = |A|I} (1)
- Find |3A| (1)
Answer:
1. |A| = \(\left[\begin{array}{ccc}{1} & {-3} & {1} \\{2} & {0} & {4} \\{1} & {2} & {-2}
\end{array}\right]\) = – 28.
2. A × adjA = |A|I
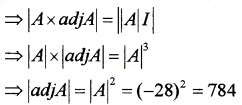
3. |3A| = 27 × |A| = 27 × -28 = -756.
Question 6.
Using properties of determinants proves the following.

Answer:


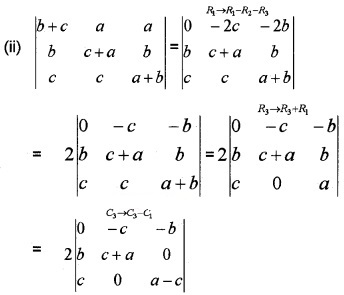
= 2{-{-c){b{a – c)) – b(-c(c + a))}
= 2{c(ab – cb) + b(c2 + ac)}
= 2{abc – c2b + bc2 + abc)} = 4abc.
Plus Two Maths Determinants Four Mark Questions and Answers
Question 1.
(i) If \(\left|\begin{array}{rrr}{1} & {-3} & {2} \\{4} & {-1} & {2} \\{3} & {5} & {2}\end{array}\right|\) = 40, then \(\left|\begin{array}{ccc}{1} & {4} & {3} \\{-3} & {-1} & {5} \\{2} & {2} & {2}\end{array}\right|\) = ?
(a) 0
(b) – 40
(c) 40
(d) 2 (1)
(ii) \(\left|\begin{array}{rrr}{3} & {-3} & {2} \\{12} & {-1} & {2} \\{9} & {5} & {2}\end{array}\right|\) = ?
(a) 120
(b) 40
(c) – 40
(d) 0 (1)
(iii) Show that ∆ = \(\left|\begin{array}{ccc}{-a^{2}} & {a b} & {a c} \\{b a} & {-b^{2}} & {b c} \\{a c} & {b c} & {-c^{2}}\end{array}\right|\) = 4a2b2c2 (2)
Answer:
(i) (c) 40
(ii) (a)120
(iii) ∆ = abc\(\left|\begin{array}{ccc}{-a} & {a} & {a} \\{b} & {-b} & {b} \\{c} & {c} & {-c}\end{array}\right|\) take a, b, c from C1, C2, C3
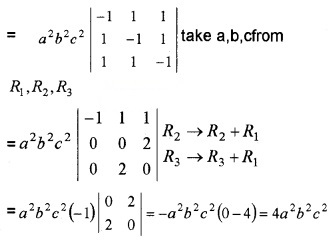
Question 2.

Answer:
(i) \(\left|\begin{array}{ll}{2} & {4} \\{5} & {1}\end{array}\right|=\left|\begin{array}{ll}{2 x} & {4} \\{6} & {x}\end{array}\right|\) ⇒ -18 = 2x2 – 24.
⇒ 2x2 = 6 ⇒ x2 = 3 ⇒ x = \(\pm \sqrt{3}\).
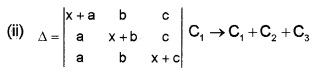
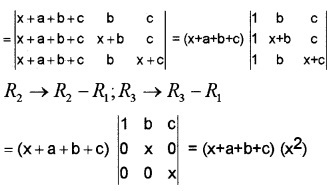
Question 3.
Prove that \(\left|\begin{array}{ccc}{(b+c)^{2}} & {a^{2}} & {a^{2}} \\{b^{2}} & {(c+a)^{2}} & {b^{2}} \\{c^{2}} & {c^{2}} & {(a+b)^{2}}\end{array}\right|\) = 2abc(a + b + c)3.
Answer:


= (a + b + c)2 × 2ab [(b + c) (c + a) – ab]
= (a + b + c)2 × 2ab [bc + ab + c2 + ac – ab)
= (a + b + c)2 × 2abc [a + b + c]
= 2abc (a + b + c)3.
Question 4.
(i) Let the value of a determinant is ∆. Then the value of a determinant obtained by interchanging two rows is
(a) ∆
(b) -∆
(c) 0
(d) 1 (1)
(ii) Show that \(\left|\begin{array}{ccc}{a+b} & {b+c} & {c+a} \\{b+c} & {c+a} & {a+b} \\{c+a} & {a+b} & {b+c}\end{array}\right|=2\left|\begin{array}{lll}{a} & {b} & {c} \\{b} & {c} & {a} \\{c} & {a} & {b}\end{array}\right|\) (3)
Answer:
(i) (b) -∆
(ii) Operating C1 → C1 + C2 + C3, we have
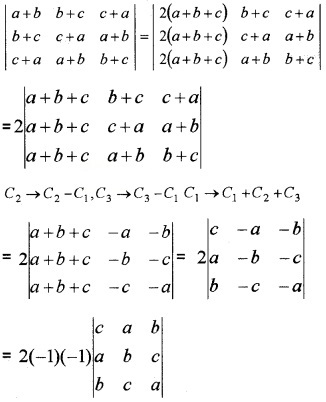

Question 5.
Test the consistency 3x – y – 2z = 2, 2y – z = -1, 3x – 5y = 3.
Answer:
The given system of equations can be put in the matrix form, AX = B, where

|A| = 3(0 – 5) + 1(0 + 3) – 2(0 – 6) = 0
C11 = -5, C12 = -3, C21 = -6, C22 = 10, C23 = 6, C31 = 12, C32 = 5, C33 = 6
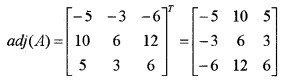

Therefore the system is inconsistent and has no solutions.
Question 6.
Consider the system of equations 2x – 3y = 7 and 3x + 4y = 5
- Express the system in AX = B form. (1)
- Find adj A (2)
- Solve the system of equations. (1)
Answer:
1. |A| = \(\left|\begin{array}{cc}{2} & {-3} \\{3} & {4}\end{array}\right|\) = 8 + 9 = 17.
2. c11 = 4, c12 = -3, c21 = 3, c22 = 2,

3. The given equations can be expressed in the form AX = B,

Question 7.
(i) If A and B are matrices of order 3 such that|A| = -1; |B| = 3, then |3AB| is
(a) -9
(b) -27
(c) -81
(d) 9 (1)
(ii) If A = \(\left[\begin{array}{cc}{1} & {\tan x} \\{-\tan x} & {1}\end{array}\right]\), Show that AT A-1 = \(\left[\begin{array}{cc}{\cos 2 x} & {-\sin 2 x} \\{\sin 2 x} & {\cos 2 x}\end{array}\right]\) (3)
Answer:
(i) (c) -81 (since |3AB| = 27|A||B|).
(ii) |A| = \(\left[\begin{array}{cc}{1} & {\tan x} \\{-\tan x} & {1}\end{array}\right]\) = sec2x ≠ 0, therefore A is invertible.
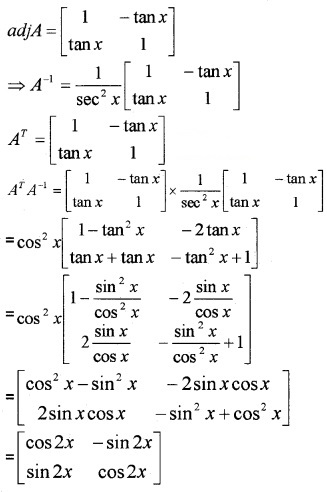
Question 8.
Consider the determinant ∆ = \(\left|\begin{array}{ccc}{x} & {x^{2}} & {1+x^{3}} \\{y} & {y^{2}} & {1+y^{3}} \\{z} & {z^{2}} & {1+z^{3}}\end{array}\right|\), Where x, y, z, are different.
(i) Express the above determinant as sum of two determinants. (1)
(ii) Show that if ∆ = 0, then 1 + xyz = 0. (3)
Answer:
(i) Given,
∆ = \(\left|\begin{array}{ccc}{x} & {x^{2}} & {1+x^{3}} \\{y} & {y^{2}} & {1+y^{3}} \\{z} & {z^{2}} & {1+z^{3}}\end{array}\right|=\left|\begin{array}{ccc}{x} & {x^{2}} & {1} \\{y} & {y^{2}} & {1} \\{z} & {z^{2}} & {1}\end{array}\right|+\left|\begin{array}{ccc}{x} & {x^{2}} & {x^{3}} \\{y} & {y^{2}} & {y^{3}} \\{z} & {z^{2}} & {z^{3}}\end{array}\right|\)

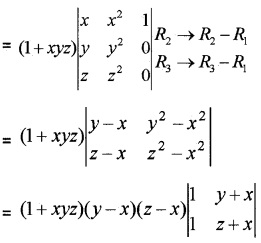
Given, ∆ = 0 ⇒ (1 + xyz)(y – x)(z – x)(z – y) = 0 ⇒ 1 + xyz = 0
∵ x ≠ y ≠ z.
Question 9.
(i) The value of the determinant \(\left|\begin{array}{cc}{\sin 10} & {-\cos 10} \\{\sin 80} & {\cos 80}\end{array}\right|\) is
(a) – 1
(b) 1
(c) 0
(d) – 2 (1)
(ii) Using properties of determinants, show that (3)
\(\left|\begin{array}{lll}{a} & {a^{2}} & {b+c} \\{b} & {b^{2}} & {c+a} \\{c} & {c^{2}} & {a+b}\end{array}\right| = (b – c) (c – a) (a – b) (a + b + c)\)
Answer:
(i) (b) Since,
sin 10 cos 80 + cos 10 sin 80 = sin (10 + 80) =sin 90 = 1.
(ii) Let C3 → C3 + C1
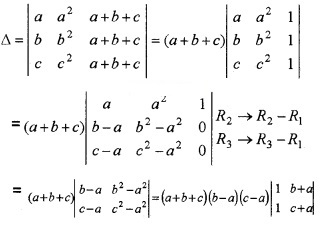
= (a + b + c)(b – a)(c – a)(c + a – b – a)
= (a + b + c)(b – a)(c – a)(c – b)
= (b – c)(c – a)(a – b)(a + b + c).
Question 10.
(i) Choose the correct answer from the bracket. Consider a square matrix of order 3. Let C11, C12, C13 are cofactors of the elements a11, a12, a13 respectively, then a11C11 + a12C12 + a13C13 is (1)
(a) 0
(b) |A|
(c) 1
(d) none of these.
(ii) Verify A(adjA) = (adjA)A = |A|I for the matrix A = \(\left[\begin{array}{ll}{5} & {-2} \\{3} & {-2}\end{array}\right]\) that, where I = \(\left[\begin{array}{ll}{1} & {0} \\{0} & {1}\end{array}\right]\) (3)
Answer:
(i) (b) |A|
(ii) |A| = \(\left|\begin{array}{cc}{5} & {-2} \\{3} & {-2}\end{array}\right|\) = – 4
C11 = – 2, C12 = – 3, C21 = 2, C22 = 5

Hence A(adjA) = (adjA)A = |A|I.
Question 11.
Consider the following system of equations x + 2y = 4,2x + 5y = 9
- If A = \(\left[\begin{array}{ll}{1} & {2} \\{2} & {5}\end{array}\right]\), find |A| (1)
- Express the above system of equations in the form AX = B (1)
- Find adj A, A-1 (1)
- Solve the system of equations. (1)
Answer:
1. |A| = \(\left[\begin{array}{ll}{1} & {2} \\{2} & {5}\end{array}\right]\) = 5 – 4 = 1
2. The given system of equation can be expressed in the form AX = B.

3. Cofactor matrix of A = \(\left[\begin{array}{cc}{5} & {-2} \\{-2} & {1}\end{array}\right]\)

4. We have,

x = 2, y = 1.
Question 12.
Consider the point X(-2, -3), B(3, 2), C(-1, -8)
- Find the area of ∆ABC (2)
- Find third vertex of any other triangle with same area and base AB. (2)
Answer:
1. \(\frac{1}{2}\left|\begin{array}{ccc}{-2} & {-3} & {1} \\{3} & {2} & {1} \\{-1} & {-8} & {1}\end{array}\right|\)
\(\frac{1}{2}\) (- 2(2 + 8) + 3(3 + 1) + 1(- 24 + 2)) = – 15
Area of ∆ ABC = 15.
2. The base AB is fixed and the third point is variable. Therefore we can choose any x coordinate and find y coordinate or vice versa.
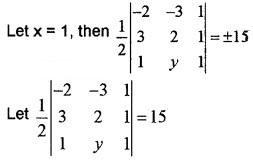
⇒ – 2(2 – y) + 3(3 – 1) + 1(3y – 2) = 30
⇒ – 4 + 2y + 6 + 3y – 2 = 30
⇒ 5y = 30 ⇒ y – 6
Therefore point is(1, 6).
Question 13.
Find the inverse of the following

Answer:
(i) Let |A| = \(\left|\begin{array}{lll}{1} & {2} & {3} \\{0} & {2} & {4} \\{0} & {0} & {5}\end{array}\right|\) = 10
C11 = 10, C12 = 0, C13 = 0, C21 = – 10, C22 = 5, C23 = 0, C31 = – 2, C32 = – 4, C33 = 2

(ii) Let |A| = \(\left|\begin{array}{ccc}{1} & {0} & {0} \\{3} & {3} & {0} \\{5} & {2} & {-1}\end{array}\right|\) = -3
C11 = -3, C12 = 3, C13 = -9, C21 = 0, C22 = -1, C23 = -2, C31 = 0, C32 = 0, C33 = 3
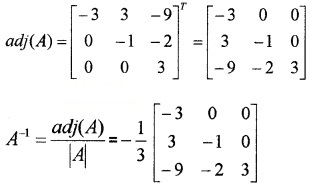
(iii) Let |A| = \(\left|\begin{array}{ccc}{2} & {1} & {3} \\{4} & {-1} & {0} \\{-7} & {2} & {1}\end{array}\right|\)
= 2(-1 – 0) -1(4 – 0) + 3(8 – 7) = -3
C11 = -1, C12 = -4, C13 = 1, C21 = 5, C22 = 23, C23 = -11, C31 = 3, C32 = 12, C33 = -6

(iv) Let |A| = \(\left|\begin{array}{ccc}{1} & {-1} & {2} \\{0} & {2} & {-3} \\{3} & {-2} & {4}\end{array}\right|\)
= 1(8 – 6) + 1(0 + 9) + 2(0 – 6) = -1
C11 = 2, C12 = -9, C13 = -6, C21 = 0, C22 = -2, C23 = -1, C31 = 3, C32 = 3, C33 = 2
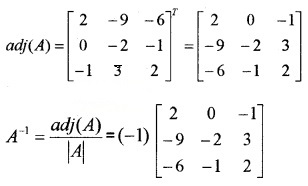
Question 14.
Consider the system of equations 5x + 2y = 4, 7x + 3y = 5. If A = \(\left[\begin{array}{ll}{5} & {2} \\{7} & {3}\end{array}\right]\), X = \(\left[\begin{array}{l}{\mathrm{r}} \\{y}\end{array}\right]\) and B = \(\left[\begin{array}{l}{4} \\{5}\end{array}\right]\)
- Find |A| (1)
- Find A-1 (2)
- Solve the above system of equations. (1)
Answer:
1. |A| = \(\left|\begin{array}{ll}{5} & {2} \\{7} & {3}\end{array}\right|\) = 15 – 14 = 1.
2. Given, A = \(\left[\begin{array}{ll}{5} & {2} \\{7} & {3}\end{array}\right]\)

3. X = A-1B
![]()
⇒ x = 2, y = -3.
Plus Two Maths Determinants Six Mark Questions and Answers
Question 1.
(i) Let A be a square matrix of order ‘n’ then |KA| = …….. (1)
(ii) Find x if \(\left|\begin{array}{cc}{x} & {2} \\{18} & {x}\end{array}\right|=\left|\begin{array}{cc}{6} & {2} \\{18} & {6}\end{array}\right|\) (2)
(iii) Choose the correct answer from the bracket. The value of the determinant \(\left|\begin{array}{ccc}{0} & {p-q} & {p-r} \\{q-p} & {0} & {q-r} \\{r-p} & {r-q} & {0}
\end{array}\right|\) is ….. (1)
(iv) Consider \(\left|\begin{array}{ccc}{a} & {a+b} & {a+b+c} \\{2 a} & {3 a+2 b} & {4 a+3 b+2 c} \\{3 a} & {6 a+3 b} & {10 a+6 b+3 c}\end{array}\right|\) (2)
Answer:
(i) If A be a square matrix of order n, then |KA| = Kn|A|
(ii) \(\left|\begin{array}{cc}{x} & {2} \\{18} & {x}\end{array}\right|=\left|\begin{array}{cc}{6} & {2} \\{18} & {6}\end{array}\right|\) ⇒ x2 – 36 = 0
⇒ x2 = 36 ⇒ x = ±6.
(iii) (c) 0 (since the given determinant is the determinant of a third order skew symmetric matrix)

= a [7a2 + 3ab – 6a2 – 3ab] = a(a2) = a3
Question 2.
(i) Let \(\left|\begin{array}{lll}{1} & {3} & {2} \\{2} & {0} & {1} \\{3} & {4} & {3}
\end{array}\right|\) = 3, then what is the value of \(\left|\begin{array}{lll}{1} & {3} & {2} \\{4} & {0} & {2} \\{3} & {4} & {3}\end{array}\right|\) = ? and\(\left|\begin{array}{lll}{6} & {7} & {6} \\{2} & {0} & {1} \\{3} & {4} & {3}\end{array}\right| \) = ? (2)
(Hint: Use the properties of determinants)
(ii) Using properties of determinants show that (4)
\(\left|\begin{array}{ccc}{1+a} & {1} & {1} \\{1} & {1+b} & {1} \\{1} & {1} & {1+c}\end{array}\right|=a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Answer:
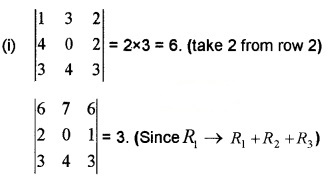
(ii) Taking ‘a’ from R1, ‘b‘ from R2,’C’ from R3

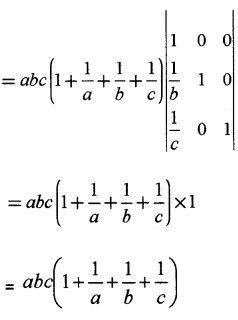
Question 3.
If A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\{3} & {2} & {-4} \\{1} & {1} & {-2}\end{array}\right]\)
- Find |A| (1)
- Find adj.A. (2)
- Solve 2x – 3y + 5z = 11, 3x + 2y – 4z = -5, x + y – 2z = -3 (3)
Answer:
1. A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\{3} & {2} & {-4} \\{1} & {1} & {-2}\end{array}\right]\)
|A| = 2 × 0 + 3x – 2 + 5 = -1.
2. Co.factor A

3. Given

i.e; AX = B ⇒ X = A-1 B

Question 4.
Let A = \(\left[\begin{array}{ccc}{1} & {-1} & {1} \\{2} & {1} & {-3} \\{1} & {1} & {1}\end{array}\right]\)
- Is A singular? (1)
- Find adj A. (2)
- Obtain A-1 (1)
- Using A-1 solve the system of equations x – y + z = 4, 2x + y – 3z = 0, x + y + z = 2 (2)
Answer:
1. A = \(\left[\begin{array}{ccc}{1} & {-1} & {1} \\{2} & {1} & {-3} \\{1} & {1} & {1}\end{array}\right]\)
⇒ |A| = 4 + 5 + 1 = 10 ≠ 0
A is non singular matrix.
2. Cofactor A

3. A-1 = \(\frac{1}{10}\) \(\left[\begin{array}{ccc}{4} & {2} & {2} \\{-5} & {0} & {5} \\{1} & {-2} {3}\end{array}\right]\)
4. Given, AX = B ⇒ X = A-1 B
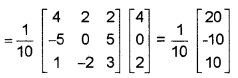
⇒ x = 2, y = -1, z = 1.
Question 5.
Solve the following system of linear equations.
- x + y + z = 3, y – z = 0, 2x – y = 1 (6)
- 5x – 6y + 4z = 15 , 7x + 4y – 3z = 19, 2x + y + 6z = 46 (6)
- x + 2y + 5z = 10, x – y – z = -2, 2x + 3_y-2 = -11 (6)
Answer:
1. Let AX = B
Where A = \(\left[\begin{array}{ccc}{1} & {1} & {1} \\{0} & {1} & {-1} \\{2} & {-1} & {0}\end{array}\right], X=\left[\begin{array}{c}{x} \\{y} \\{z}\end{array}\right], B=\left[\begin{array}{l}{3} \\{0} \\{1}\end{array}\right]\)
|A| = 1(0 – 1) – 1(0 + 2) + 1(0 – 2) = -5
C11 = -1, C12 = -2, C13 = -2, C21 = -1, C22 = 3, C23 = 3, C31 = -2, C32 = 1, C33 = 1

2. Let AX = B,
Where A = \(\left[\begin{array}{ccc}{5} & {-6} & {4} \\{7} & {4} & {-3} \\{2} & {1} & {6}\end{array}\right], X=\left[\begin{array}{c}{x} \\{y} \\{z}\end{array}\right],B=\left[\begin{array}{c}{15} \\{19} \\{46}\end{array}\right]\)
|A| = 5(24 + 3) + 6(42 + 6) + 4(7 – 8) = 419
C11 = 27, C12 = -48, C13 = -1, C21 = -1, C22 = 22, C23 = -17, C31 = 2, C32 = 43, C33 = 62


3. Let AX = B
\(\text { Where } A=\left[\begin{array}{ccc}{1} & {2} & {5} \\{1} & {-1} & {-1} \\{2} & {3} & {-1}
\end{array}\right], X=\left[\begin{array}{c}{x} \\{y} \\{z}\end{array}\right], B=\left[\begin{array}{c}{10} \\{-2} \\{-11}\end{array}\right]\)
|A| = 1(4) – 2(1) + 5(5) = 27
C11 = 4, C12 = -1, C13 = 5, C21 = 17, C22 = -11, C23 = 1, C31 = 3, C32 = 6, C33 = -3

⇒ x = -1, y = -2, z = 3.
Question 6.
If f(x) = \(\left[\begin{array}{ccc}{\cos x} & {-\sin x} & {0} \\{\sin x} & {\cos x} & {0} \\{0} & {0} & {1}\end{array}\right]\)
(i) Find f(-x) (2)
(ii) Find (f(x)]-1 (2)
(iii) Is |f(x)]-1 = f(-x)? (2)
Answer:

(ii) |f(x)| = \(\left[\begin{array}{ccc}{\cos x} & {-\sin x} & {0} \\{\sin x} & {\cos x} & {0} \\{0} & {0} & {1}\end{array}\right]\) = cos x (cos x) + sin x (sin x) = 1 ≠ 0
Therefore , [f(x)]-1 exists.
The cofactors are as follows.
C11 = cos x, C12 = -sin x, C13 = 0, C21 = sin x, C22 = cos x, C23 = 0, C31 = 0, C32 = 0, C33 = 1

Since, |f(x)|= 1
(iii) Yes. From (1) and (2) we have,
[f(x)]-1 =f(-x).
Question 7.
(i) Choose the correct answer from the bracket. If A = \(\left[\begin{array}{cc}{2} & {3} \\{1} & {-2}\end{array}\right]\) and A-1 = kA, then the value of ‘k’ is
(a) 7
(b) -7
(c) \(\frac{1}{7}\)
(d)\(-\frac{1}{7}\) (1)
(ii) If A = \(\left[\begin{array}{ccc}{1} & {-1} & {1} \\{2} & {-1} & {0} \\{1} & {0} & {0}
\end{array}\right]\),
(a) A2 (2)
(b) Show that A2 = A-1 (3)
Answer:


C11 = 0, C12 = 0, C13 = 1, C21 = 0, C22 = -1, C23 = -1, C31 = 1, C32 = 2, C33 = 1
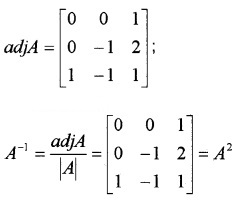
Question 8.
‘Arjun’ purchased 3 pens, 2 purses, and 1 instrument box and pays Rs. 410. From the same Shop ‘Deeraj’ purchases 2 pens, 1 purse, and 2 instrument boxes and pays Rs.290, while ‘Sindhu’ purchases 2pens, 2 purses, 2 instrument boxes and pays Rs. 440.
- Translate the equation into system of linear equations. (2)
- The cost of one pen, one purse and one instrument box using matrix method. (4)
Answer:
1. Let The price of one pen is Rs.x, one purse is Rs.y and one instrument box be Rs.z
3x + 2y + z = 410; 2x + y + 2z =290; 2x + 2y + 2z = 440(1) 2 mts.
2. The system can be represented by the matrix equation AX = B

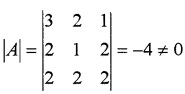
C11 = -2, C12 = 0, C13 = 2, C21 = -2, C22 = 4, C23 = -2, C31 = 3, C32 = -4, C33 = -1

Hence the cost one pen is Rs.20, one purse is Rs. 150 and one instrument box is Rs. 50.
Question 9.
If A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\{3} & {2} & {-4} \\{1} & {1} & {-2}\end{array}\right]\)
- Find A-1 (3)
- Using it solve the system of equations 2x – 3y + 5z = 16, 3x + 2y – 4z = -4, x + y – 2z = -3 (3)
Answer:
1. A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\{3} & {2} & {-4} \\{1} & {1} & {-2}\end{array}\right]\)
⇒ |A| = 0 + 3x – 2 + 5 = -1

2. Given AX = B
⇒ X = A-1B

⇒ x = 2, y = 1, z = 3.
Question 10.
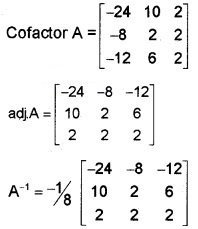
Consider the following system of equations x + y + 3z = 5, x + 3y – 3z = 1, -2x – 4y – 4z = -10
(i) Convert the given system in the form AX = B (1)
(ii) Find A-1 (3)
(iii) Hence solve the system of equations. (2)
Answer:

(ii) i.e; AX = B, ⇒ X = A-1 B ⇒ |A| = -24 + 10 + 6 = -8
(iii) X = A-1B

= \(-\frac{1}{8}\) \(\left[\begin{array}{l}{-8} \\{-8} \\{-8}\end{array}\right]\)
⇒ x = 1, y = 1, z = 1.
Question 11.
Solve the following system by equations by matrix method x + 2y + 5z = 10; x – y – z = -2; 2x + 3y – z = -11.
Answer:
x + 2y + 5z = 10; x – y – z = -2; 2x + 3y – z = 11

⇒ x = -1, y = -2, z = 3.
Question 12.
If A = \(\left[\begin{array}{ccc}{3} & {-2} & {3} \\{2} & {1} & {-1} \\{4} & {-3} & {2}\end{array}\right]\)
- Find |A| (1)
- Find A-1 (3)
- Solve the linear equations 3x – 2y + 3z = 8; 2x + y – z = 1; 4x – 3y + 2z = 4 (2)
Answer:
1. |A| = \(\left[\begin{array}{ccc}{3} & {-2} & {3} \\{2} & {1} & {-1} \\{4} & {-3} & {2}\end{array}\right]\)
= 3(2 – 3) + 2(4 + 4) + 3(- 6 – 4) = -17.
2. |A| ≠ 0, hence its inverse exists.
A-1 = \(\frac{1}{|A|}\)adj A
C11 = -1, C12 = -8, C13 = -10, C21 = -5, C22 = -6, C23 = 1, C31 = -1, C32 = 9, C33 = 7

3. The given system of linear equations is of the form
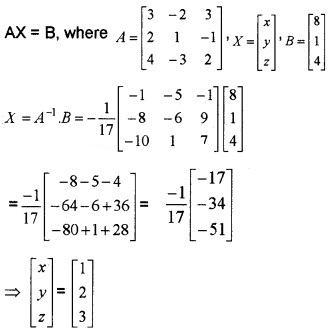
∴ We have, x = 1, y = 2, z = 3.
Question 13.
if \(\left[\begin{array}{cc}{2} & {5} \\{-3} & {7}\end{array}\right] \times A=\left[\begin{array}{cc}{17} & {-1} \\{47} & {-13}\end{array}\right]\) then
(i) Find the 2 × 2 matrix A. (3)
(ii) Find A2. (1)
(iii) Show that A2 + 5A – 6I = 0, where I is the identity matrix of order 2. (2)
Answer:
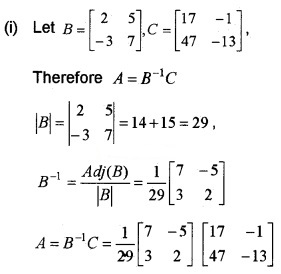



We hope the given Plus Two Maths Chapter Wise Questions and Answers Chapter 4 Determinants will help you. If you have any query regarding Plus Two Maths Chapter Wise Questions and Answers Chapter 4 Determinants, drop a comment below and we will get back to you at the earliest.